6.1. Точечные оценки неизвестных параметров распределений и требования, предъявляемые к ним

При точечном оценивании ищут статистику , (т.е. функцию, зависящую только от выборки ), значение которой при заданной выборке принимают за приближенное значение неизвестного параметра . В этом случае статистику называют оценкой параметра .

Естественно, оценка зависит от объема выборки : . Однако далее в обозначениях эта зависимость будет присутствовать в явном виде только при исследовании асимптотических (при ) свойств оценки.

Обосновать качество оценки можно лишь исходя из ее свойств, не зависящих от конкретной выборки. Для изучения таких свойств вероятностного характера в соответствии с замечанием из раздела 1 под оценкой следует понимать случайную величину , получаемую заменой выборочных значений на случайные величины - копии наблюдаемой случайной величины .

Для оценивания одного и того же параметра можно использовать различные оценки . Выбор из множества оценок наилучшей основан на критерии сравнения качества оценок, предложенном Р.А.Фишером. Согласно этому критерию к оценкам неизвестных параметров распределений предъявляются следующие требования.

1. Несмещенность

Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру : .

Ошибку , возникающую в результате замены неизвестного параметра известной оценкой можно представить в виде:

,

где - случайная ошибка оценивания, а - систематическая ошибка, называемая смещением оценки .

Таким образом, несмещенность оценки означает отсутствие систематической ошибки в соответствующих результатах оценивания или, что эквивалентно, отсутствие смещения: для любого . Несмещенная оценка по крайней мере «в среднем» приводит к желаемому результату. Однако требование несмещенности не следует преувеличивать, иногда бывает разумно от него и отказаться.

Оценка , у которой при , называется асимптотически несмещенной.

2. Состоятельность

Оценка называется состоятельной, если при возрастании объема выборки она сходится по вероятности к истинному значению неизвестного параметра : .

Свойство состоятельности является обязательным для любой оценки, поскольку при увеличении объема информации оценка должна быть ближе к истине. Однако, по существу, свойство состоятельности является асимптотическим и не связано со свойствами оценки при фиксированном объеме выборки.

Для несмещенной оценки в силу неравенства Чебышева

.

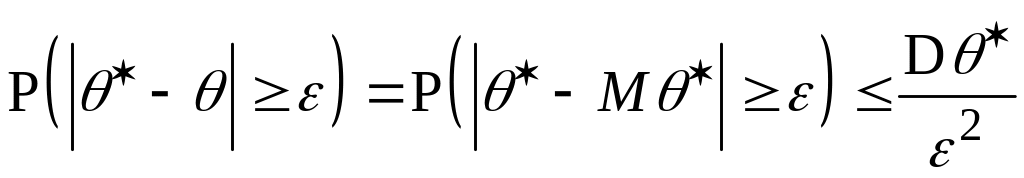Поэтому достаточным условием состоятельности несмещенной оценки является стремление к нулю ее дисперсии:

.

Эффективность

Может существовать несколько несмещенных и состоятельных оценок одного и того же неизвестного параметра . Тогда из них следует отдать предпочтение той, которая имеет меньшую дисперсию, поскольку дисперсия характеризует разброс значений оценки около истинного значения параметра .

Пусть - класс всех состоятельных и несмещенных оценок параметра , имеющих конечную дисперсию. Оценка называется более эффективной, чем оценка , если для любого .

Оценка , имеющая минимальную дисперсию среди всех оценок из класса , называется эффективной оценкой параметра , то есть

.

В общем случае точность оценки характеризуется ее среднеквадратической погрешностью

.

Для среднеквадратической погрешности также справедливо представление:

.

Эффективные оценки представляют особенно большой практический интерес, поскольку, являясь несмещенными, они дают наименьшую среднеквадратическую погрешность оценивания. Если оценка не является несмещенной ( ), то малость ее дисперсии еще не говорит о малости ее среднеквадратической погрешности (например, если оценка , то , однако погрешность оценивания может быть сколь угодно большой). Тем не менее, среднеквадратическая погрешность оценки с небольшим смещением может оказаться меньше, чем у оценки несмещенной, за счет существенно меньшей ее дисперсии. Этот факт является объяснением тому, что для уменьшения суммарной ошибки оценивания от требования несмещенности оценки бывает разумно и отказаться.

Эффективность оценки позволяет установить следующее неравенство Рао-Крамера: для широкого класса непрерывных распределений и для любой несмещенной оценки , имеющей конечную дисперсию, справедливо неравенство:

,

где - плотность вероятностей наблюдаемой случайной величины , - информация Фишера о параметре , содержащаяся в одном наблюдении над случайной величиной .

Таким образом, оценка является эффективной, если она обращает неравенство Рао-Крамера в равенство, т.е. .