4. Гистограмма и полигон частот.

Пусть - выборка объема из генеральной совокупности, имеющей непрерывное распределение с неизвестной (теоретической) плотностью вероятностей . Способом представления статистических данных, дающим наглядное представление о плотности вероятностей (статистическим аналогом ), является гистограмма. Для ее построения следует предварительно произвести группировку данных, которая состоит в следующем:

1. По данной выборке строят вариационный ряд

.

2. Промежуток разбивают точками на непересекающихся интервалов , так что 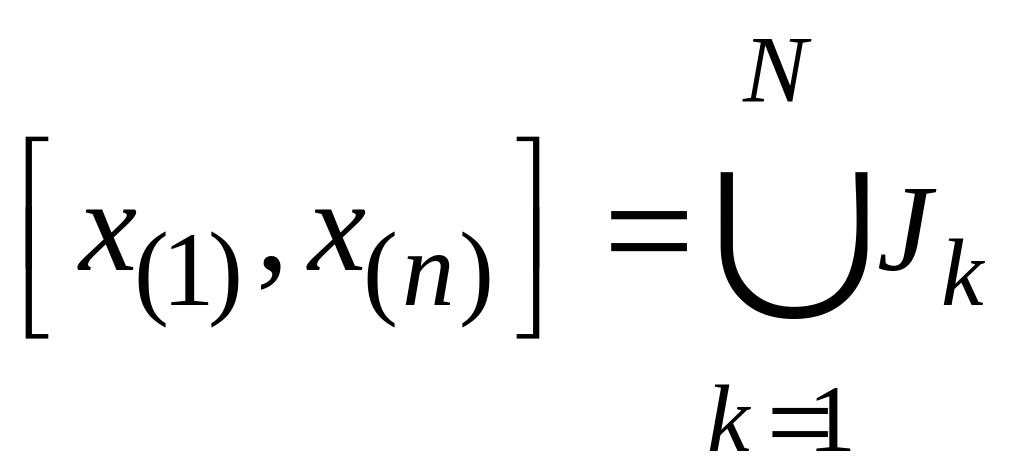(на практике существенно меньше ).

3. Подсчитывают частоты и относительные частоты 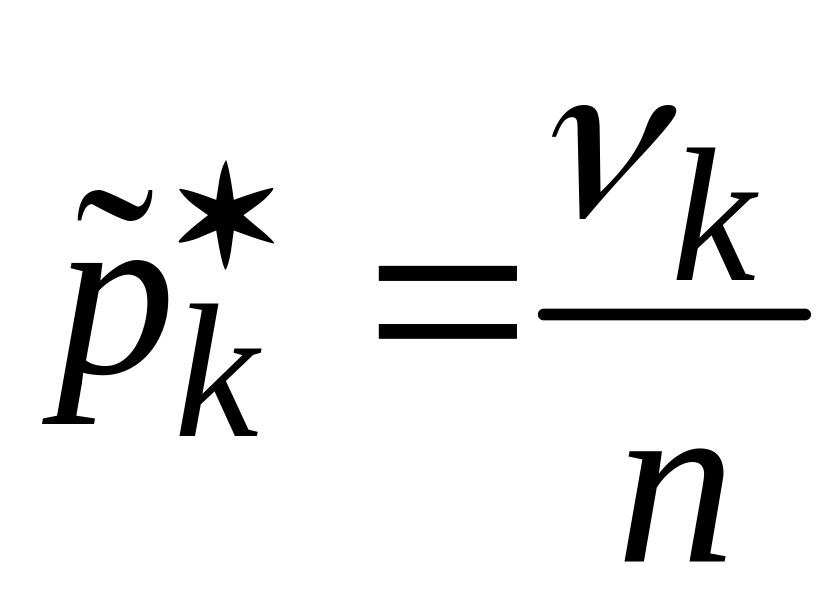попадания выборочных значений в -ый интервал , .

4. Полученную информацию заносят в таблицу, называющуюся интервальным статистическим рядом:

Интервалы			…
Частоты			…
Относительные частоты			…

Очевидно, что . Поэтому совокупность пар , где 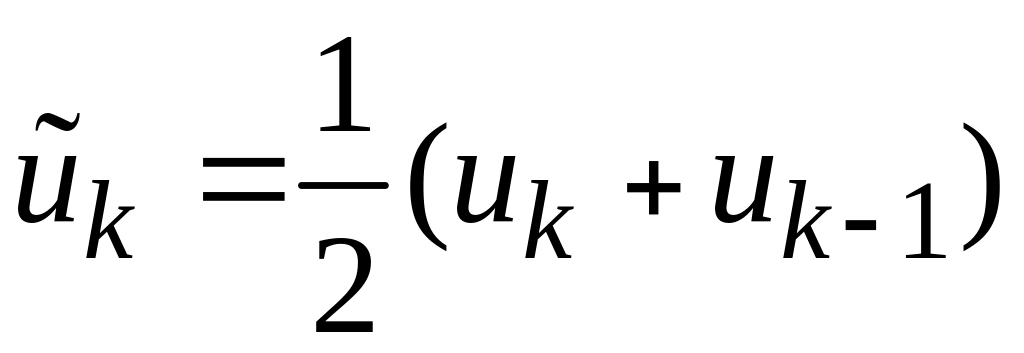- середина интервала , , называют эмпирическим законом распределения, полученным по сгруппированным данным.

Далее в прямоугольной системе координат на каждом интервале , как на основании длиной , строят прямоугольник с высотой . Получаемую при этом ступенчатую фигуру называют гистограммой.

Площадь, ограниченная верхней границей гистограммы и осью абсцисс, равна 1, так как .

Частоты , меняются от выборки к выборке, являясь в общем случае случайными величинами. В силу теоремы Бернулли при каждом , относительные частоты , где - истинная вероятность попадания наблюдаемой случайной величины в интервал .

Если длины интервалов достаточно малы, а теоретическая плотность вероятностей непрерывна, то по теореме о среднем . Следовательно, при большом объеме выборки и достаточно малом справедливо приближенное равенство 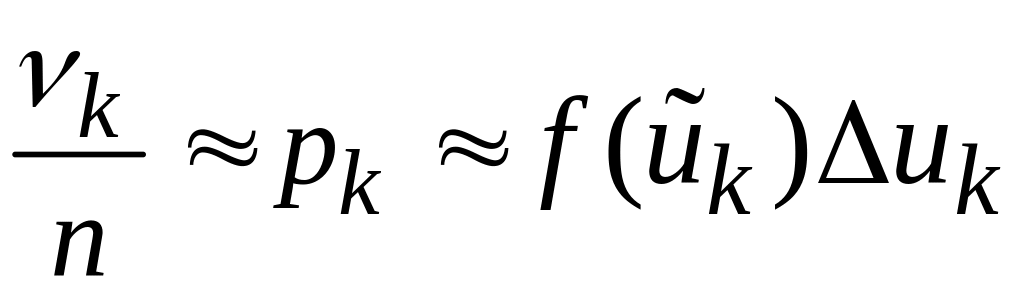или, что эквивалентно, .

Поэтому верхняя граница гистограммы является статистическим аналогом (оценкой) неизвестной плотности вероятностей наблюдаемой случайной величины .

Построение гистограммы, как способ представления статистических данных, рекомендуется применять только в непрерывной статистической модели наблюдений. При этом, он обладает следующими очевидными недостатками:

- потерей информации при группировке статистических данных (при построении используются не сами выборочные значения , а частоты попадания выборочных значений в интервалы группировки);

- неопределенностью в способе построения интервалов группировки и определении их числа и длин (на практике при группировке данных обычно для простоты берут интервалы одинаковой длины = = соnst, а число интервалов группировки определяют с помощью установленного эмпирическим путем правила Стургерса, согласно которому полагается , но эти рекомендации не являются оптимальными в каком-либо смысле в общем случае).

Поэтому гистограмму следует применять только на предварительном этапе анализа статистических данных.

Замечание. Иногда к группировке данных прибегают и в случае дискретной модели наблюдений. Это делают при большом , когда простой статистический ряд трудно обозрим. Но в этом случае число интервалов нужно брать тоже большим, чтобы избежать существенных неточностей при замене настоящего эмпирического закона распределения на эмпирический закон распределения, полученный по сгруппированным данным. Следует также понимать, что в дискретной модели наблюдений гистограмма – это просто частотно-графический способ представления статистических данных, а вероятностный смысл гистограммы, как оценки плотности вероятностей, отсутствует.

Гистограмма является кусочно-постоянным приближением неизвестной (теоретической) плотности вероятностей . Если плотность вероятностей является гладкой функцией, то, как известно из математического анализа, ее значительно лучше можно аппроксимировать кусочно-линейной функцией. Ломаная с вершинами в точках , называется полигоном частот и является для гладких плотностей вероятностей более точной оценкой, чем гистограмма. Пример гистограммы и полигона частот приведен на рисунке 1.

Р исунок 1 - Гистограмма и полигон частот