
- •Математическая статистика
- •1. Статистическая модель и задачи математической статистики
- •2. Способы представления статистических данных.
- •3. Эмпирическая функция распределения и ее свойства.
- •4. Гистограмма и полигон частот.
- •5. Выборочные (эмпирические) числовые характеристики
- •6. Оценивание неизвестных параметров распределений
- •6.1. Точечные оценки неизвестных параметров распределений и требования, предъявляемые к ним
- •Несмещенность
- •Состоятельность
- •6.2. Свойства выборочного среднего и выборочной дисперсии
- •6.3. Методы нахождения точечных оценок
- •6.3.1. Метод моментов
- •6.3.2. Метод максимального правдоподобия
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Федеральное государственное бюджетное учреждение высшего профессионального образования
«Самарский государственный аэрокосмический университет имени академика с.п. королева»
(национальный исследовательский университет)
Математическая статистика
Конспект лекций
по курсу
«Теория вероятностей и математическая статистика»
Лектор:
к.ф.-м.н., доцент
Коломиец Э.И.
САМАРА 2014
1. Статистическая модель и задачи математической статистики
Математическая статистика – раздел прикладной математики, непосредственно примыкающий и основанный на теории вероятностей. Как и любая математическая теория, математическая статистика развивается в рамках некоторой модели, описывающей определенный круг реальных явлений. Чтобы определить статистическую модель и объяснить специфику задач математической статистики, напомним некоторые положения из теории вероятностей.
Математическая
модель случайных явлений, изучаемых в
теории вероятностей, основывается на
понятии вероятностного пространства
![]() .
При этом в каждой конкретной ситуации
вероятность
.
При этом в каждой конкретной ситуации
вероятность
![]() считается полностью известной числовой
функцией на
считается полностью известной числовой
функцией на
![]() -алгебре
-алгебре
![]() ,
то есть для любого
,
то есть для любого
![]() полностью определено число
полностью определено число
![]() .
Основной задачей теории вероятностей
является разработка методов нахождения
вероятностей различных сложных событий
по известным вероятностям более простых
(например, по известным законам
распределения случайных величин
определяются их числовые характеристики
и законы распределения функций от
случайных величин).
.
Основной задачей теории вероятностей
является разработка методов нахождения
вероятностей различных сложных событий
по известным вероятностям более простых
(например, по известным законам
распределения случайных величин
определяются их числовые характеристики
и законы распределения функций от
случайных величин).
Однако
на практике при изучении конкретного
случайного эксперимента вероятность
,
как правило, неизвестна или известна
частично. Можно только предположить,
что истинная вероятность
является элементом некоторого класса
вероятностей
![]() (в худшем случае
- класс всевозможных вероятностей,
которые можно задать на
).
Класс
называют совокупностью допустимых
для описания
данного эксперимента вероятностей
,
а набор
(в худшем случае
- класс всевозможных вероятностей,
которые можно задать на
).
Класс
называют совокупностью допустимых
для описания
данного эксперимента вероятностей
,
а набор
![]() - статистической
моделью эксперимента.
В общем случае задачей математической
статистики является уточнение
вероятностной модели изучаемого
случайного явления (то есть отыскание
истинной или близкой к ней вероятности
),
используя информацию, доставляемую
наблюдаемыми исходами эксперимента,
которые называют статистическими
данными.
- статистической
моделью эксперимента.
В общем случае задачей математической
статистики является уточнение
вероятностной модели изучаемого
случайного явления (то есть отыскание
истинной или близкой к ней вероятности
),
используя информацию, доставляемую
наблюдаемыми исходами эксперимента,
которые называют статистическими
данными.
В
классической математической статистике,
изучением которой мы будем заниматься
далее, имеют дело со случайными
экспериментами, состоящими в проведении
n
повторных
независимых наблюдений над некоторой
случайной величиной
![]() ,
имеющей неизвестное распределение
вероятностей, т.е. неизвестную функцию
распределения
,
имеющей неизвестное распределение
вероятностей, т.е. неизвестную функцию
распределения
![]() .
В этом случае множество
.
В этом случае множество
![]() всех
возможных значений наблюдаемой случайной
величины
называют генеральной
совокупностью,
имеющей функцию распределения
всех
возможных значений наблюдаемой случайной
величины
называют генеральной
совокупностью,
имеющей функцию распределения
![]() или распределенной
согласно
.
Числа
или распределенной
согласно
.
Числа
![]() ,
являющиеся результатом
,
являющиеся результатом
![]() независимых наблюдений над случайной
величиной
,
называют выборкой
из генеральной совокупности или
выборочными
(статистическими)
данными. Число наблюдений
называется объемом
выборки.
независимых наблюдений над случайной
величиной
,
называют выборкой
из генеральной совокупности или
выборочными
(статистическими)
данными. Число наблюдений
называется объемом
выборки.
Основная задача математической статистики состоит в том, как по выборке из генеральной совокупности, извлекая из нее максимум информации, сделать обоснованные выводы относительно неизвестных вероятностных характеристик наблюдаемой случайной величины .
Под
статистической моделью, отвечающей
повторным независимым наблюдениям над
случайной величиной
,
естественно, вместо
понимать набор
![]() ,
где
,
где
![]() - генеральная совокупность,
- генеральная совокупность,
![]() -
-алгебра
борелевских подмножеств из
,
-
-алгебра
борелевских подмножеств из
,
![]() - класс допустимых функций распределения
для данной случайной величины
,
которому принадлежит и истинная
неизвестная функция распределения
.
- класс допустимых функций распределения
для данной случайной величины
,
которому принадлежит и истинная
неизвестная функция распределения
.
Часто тройку называют статистическим экспериментом.
Если
функции распределения из
заданы с точностью до значений некоторого
параметра
![]() ,
то есть
,
то есть
![]() (
(![]() - параметрическое множество), то такая
модель называется параметрической.
Говорят, что в этом случае известен тип
распределения наблюдаемой случайной
величины, а неизвестен только параметр,
от которого распределение зависит.
Параметр
может быть как скалярным, так и векторным.
- параметрическое множество), то такая
модель называется параметрической.
Говорят, что в этом случае известен тип
распределения наблюдаемой случайной
величины, а неизвестен только параметр,
от которого распределение зависит.
Параметр
может быть как скалярным, так и векторным.
Статистическая модель называется непрерывной или дискретной, если таковыми являются все составляющие класс функции распределения соответственно.
Пример
1. Предположим,
что распределение наблюдаемой случайной
величины
является гауссовским с известной
дисперсией
![]() и неизвестным
математическим ожиданием
.
и неизвестным
математическим ожиданием
.
В этом случае статистическая модель является непрерывной и имеет вид:
![]() ,
где
,
где
![]() ,
,
а
функция распределения
![]() имеет плотность вероятностей
имеет плотность вероятностей
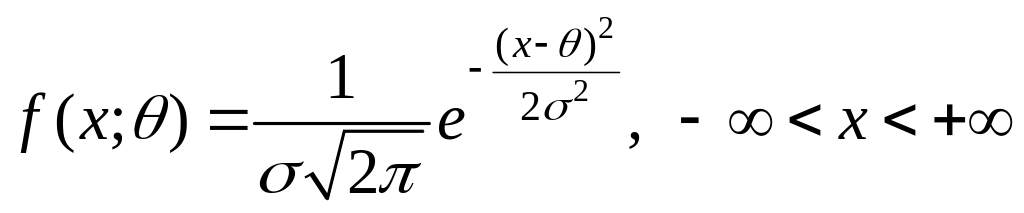 .
.
Далее
для этой модели будем использовать
обозначение
![]() .
.
Если и дисперсия неизвестна, то статистическая модель имеет вид:
,
где
![]() ,
,
а функция распределения имеет плотность вероятностей
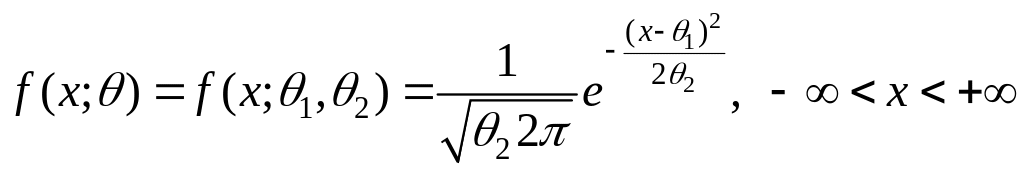 .
.
Это,
так называемая, общая нормальная модель,
обозначаемая
![]() .
.
Пример 2. Предположим, что распределение наблюдаемой случайной величины является пуассоновским с неизвестным параметром . В этом случае статистическая модель является дискретной и имеет вид:
,
где
![]() ,
,
а функция распределения определяется вероятностями
 .
.
Эта
модель называется пуассоновской и
обозначается
![]() .
.
Замечание:
Выборка
является
исходной информацией для статистического
анализа и принятия решений о неизвестных
вероятностных характеристиках наблюдаемой
случайной величины
.
Однако на основе конкретной выборки
обосновать качество статистических
выводов принципиально невозможно. Для
этого на выборку следует смотреть
априорно как на случайный
вектор
![]() ,
координаты которого являются независимыми,
распределенными так же как и
,
случайными величинами (при этом говорят,
что случайные величины
,
координаты которого являются независимыми,
распределенными так же как и
,
случайными величинами (при этом говорят,
что случайные величины
![]() - копии
),
и который еще не принял конкретного
значения в результате эксперимента.
Переход от выборки конкретной
к выборке случайной
будет неоднократно использоваться
далее при решении теоретических вопросов
и задач для получения выводов, справедливых
для любой выборки из генеральной
совокупности.
- копии
),
и который еще не принял конкретного
значения в результате эксперимента.
Переход от выборки конкретной
к выборке случайной
будет неоднократно использоваться
далее при решении теоретических вопросов
и задач для получения выводов, справедливых
для любой выборки из генеральной
совокупности.
Основные задачи, рассматриваемые в математической статистике, можно разбить на две большие группы:
Задачи, связанные с определением неизвестного закона распределения наблюдаемой случайной величины и параметров в него входящих (они рассматриваются в рамках статистической теории оценивания).
Задачи, связанные с проверкой гипотез относительно закона распределения наблюдаемой случайной величины (решаются в рамках теории проверки статистических гипотез).
