35. Параллельные соединения r и с и r и l элементов.

1) Параллельное соединение резистивного и емкостного элементов

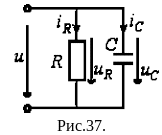
    Для цепи на рис. 37 имеют место соотношения: ;

, где  [См] – активная проводимость;

, где  [См] – реактивная проводимость конденсатора.

Векторная диаграмма токов для данной цепи, называемая треугольником токов, приведена на рис. 38. Ей соответствует уравнение в комплексной форме:

,

где ;  – комплексная проводимость,

.

     

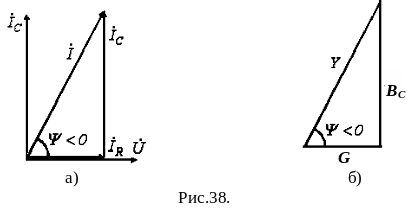
Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 38 б.

Для комплексного сопротивления цепи на рис.38 б можно записать

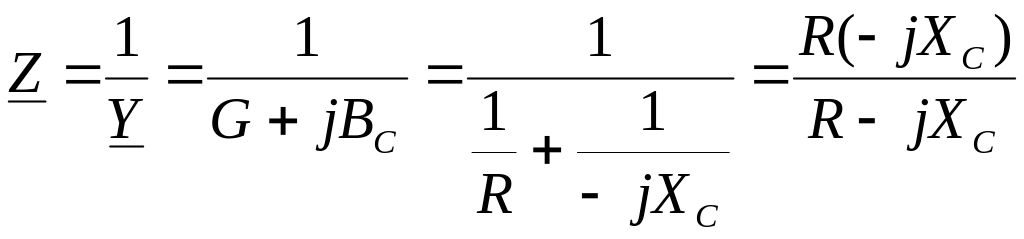
Полученный результат аналогичен известному из курса физики выражению для эквивалентного сопротивления двух параллельно соединенных резисторов.

2) Параллельное соединение резистивного и индуктивного элементов

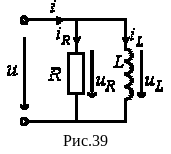
Для цепи на рис. 39 можно записать: ;

, где  [См] – активная проводимость;

, где  [См] – реактивная проводимость катушки индуктивности.

Векторной диаграмме токов (рис. 40 а) для данной цепи соответствует уравнение в комплексной форме

,

где ;  – комплексная проводимость,

.

Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 40б. Выражение комплексного сопротивления цепи на рис. 40 б имеет вид:

Полученный результат также аналогичен известному из курса физики выражению для эквивалентного сопротивления двух параллельно соединенных резисторов.

36. Резонанс токов.

Р езонанс токов может возникнуть в параллельной цепи (рис. 41), одна из ветвей которой содержит L и R, а другая – С и R.

Положим, что заданы величины R₁, R₂, L, С, частота f и входное напряжение U. Требуется определить токи в ветвях и ток всей цепи.

В данной схеме две ветви. Согласно свойству параллельного соединения, напряжение на всех ветвях параллельной цепи одинаковое, если пренебречь сопротивлением подводящих проводов.

Задача разбивается на ряд этапов

1. Определение сопротивлений ветвей. Реактивные сопротивления элементов L и С определяем по формулам X_L = ωL, X_C = 1 / ωC, ω = 2πf.

Полное сопротивление ветвей равны: , ,

соответствующие им углы сдвига фаз φ₁ = arctg(X_L / R₁), φ₂ = arctg(X_С / R₂).

2. Нахождение токов в ветвях. По закону Ома: I₁ = U / Z₁, Ψ_i1 = Ψ_U + φ₁,

I₂ = U / Z₂, Ψ_i2 = Ψ_U + φ₂.

3. Нахождение тока всей цепи.

Т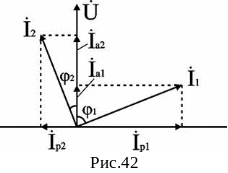 ок всей цепи может быть найден несколькими методами: графическим, методом мощностей, методом проекций и методом проводимостей.

Чаще всего используют метод проекций и метод проводимостей. В методе проекций ток I₁ и I₂ раскладываются по две ортогональные составляющие активную и реактивную. Ось активной составляющей совпадает с вектором напряжения U. Ось реактивной составляющей перпендикулярна вектору U (рис. 42).

Активные составляющие токов равны:

, ;

Реактивные составляющие токов равны:

,

В последнем уравнении взят знак минус, поскольку составляющие I_1р (индуктивная) и I_2р (емкостная) направлены в разные стороны от оси U.

Полный ток находится из уравнений: , φ = arctg(I_р / I_а).

В методе проводимостей также используется разложение на активные и реактивные составляющие. Используя уравнение (2.30) активные составляющие токов записываются в виде: ,

где через G₁ = R₁ / Z₁² обозначена величина, названная активной проводимостью первой ветви. Аналогичным образом получим ,

где G₂ = R₂ / Z₂²; а величину G = G₁ + G₂ называют активной проводимостью всей цепи.

Запишем реактивные составляющие токов

,

где B₁ и B₂ – реактивные проводимости ветвей: B₁ = X_L / Z₁², B₂ = X_C / Z₂².

Для реактивной проводимости всей цепи имеем B = B₁ – B₂.

В этом уравнении взят знак минус, из тех же соображений, как и в уравнении метода проекций. Величина тока I и угол φ находятся из соотношений

, φ = arctg(I_р / I_а).

4. Анализ расчетных данных. В зависимости от соотношения реактивных проводимостей B₁ и B₂ возможны три варианта: B₁ > B₂; B₁ < B₂; B₁ = B₂.

Для варианта B₁ > B₂ имеем I_1р > I_2р, φ > 0. Цепь имеет активно-индуктивный характер. Векторная диаграмма изображена на рис. 43 а.

При B₁ < B₂ токи I_1р < I_2р, φ < 0. Цепь имеет активно-емкостный характер. Векторная диаграмма изображена на рис.43 б.

Если B₁ = B₂, то I_1р = I_2р, φ = 0. Цепь имеет чисто активное сопротивление. Ток, потребляемый цепью от источника, наименьший. Этот режим называется резонанс токов. Векторная диаграмма изображена на рис. 43 в.

Резонансом токов называется такое состояние цепи, когда общий ток совпадает по фазе с напряжением, реактивная мощность равна нулю и цепь потребляет только активную мощность.

При резонансе токов коэффициент мощности равен единице: cos =1. Полная мощность равна активной мощности: S = Р.

Реактивная мощность равна нулю: Q = Q_L –Qc = 0.

Общий реактивный ток цепи, равный разности реактивных токов ветвей, в этом случае равен нулю: . Общий ток цепи имеет только активную составляющую, равную сумме активных составляющих токов ветвей: .

При резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи рис. 94 резистора ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе в цепи минимален:

, – резонансная частота.

Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений.

Реактивная энергия действует внутри цени: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода энергия электрического поля емкости переходит в энергию магнитного поля индуктивности. Обмена реактивной энергией между потребителями цепи и источником питания не происходит. Ток в проводах, соединяющих цепь с источником, обусловлен только активной мощностью.

Для резонанса токов характерно, что общий ток при определенном сочетании параметров цепи может быть значительно меньше токов в каждой ветви. Например, в идеальной цепи, когда г\ = ri = 0, общий ток равен нулю, а токи ветвей с емкостью и индуктивностью существуют: они равны по модулю и сдвинуты по фазе на 180°. Резонанс в цепи при параллельном соединении потребителей называется резонансом токов.

Резонанс токов может быть получен путем подбора параметров цепи при заданной частоте источника питания или путем подбора частоты источника питания при заданных параметрах цепи.