Основные показатели надежности невосстанавливаемых (неремонтируемых) систем

Для невосстанавливаемых систем, чаще всего, используются четыре показателя надежности: вероятность безотказной работы P(t), плотность вероятности отказов (частота отказов) f(t), интенсивность отказов λ(t), среднее время безотказной работы (средняя наработка на отказ) T₀.

Вероятность безотказной работы P(t) есть вероятность того, что время работы системы до отказа окажется больше заданного времени t.

,                                  (3.1)

где  Т – случайное время работы системы до отказа или наработка на отказ;

 – интегральная функция распределения случайной величины Т (T < t).

Иногда пользуются понятием вероятности отказов Q(t):

.                                       (3.2)

Если P(t) – надежность системы, то Q(t) – ненадежность системы.

Плотность вероятности, или частота отказов, является дифференциальной функцией распределения.

.                                    (3.3)

Интенсивность отказа λ(t) – это отношение плотности вероятности к вероятности безотказной работы:

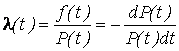,                                      (3.4)

откуда

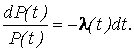
 если λ = const,                     (3.5)

Среднее время безотказной работы системы – это математическое ожидание времени работы системы до отказа:

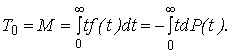
Пределы несобственного интеграла изменяются от 0 до ∞, так как время не может быть отрицательным.

Интегрируем по частям, получим

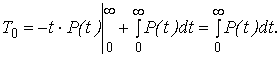                            (3.6)

, так как при верхнем пределе P(t) быстрее стремится к нулю, чем t стремится к бесконечности.

На рис. 3.1 изображена зависимость вероятности безотказной работы от времени. В начальный момент вероятность Р равна единице. В конце времени работы системы Т вероятность равна нулю.

 

П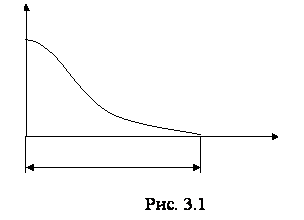 оказатели надежности функционально связаны между собой: зная одну из функций P(t), Q(t), f(t), λ(t), можно определить три остальные.

Статистические показатели надежности невосстанавливаемых систем, получаемые из экспериментальных данных, можно определить по следующим формулам:

 - статистическая вероятность безотказной работы

,                                                    (3.7)

где  N – число объектов в начале испытаний;

n_i – число объектов, отказавших за время t_i.

Под частотой отказов элементов понимают число отказов в единицу времени, отнесенное к первоначальному количеству поставленных на испытания элементов.

- статистическая частота отказов

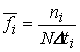,                                                     (3.8)

где  n_i – число отказов в интервале времени ∆t_i;

N – число испытуемых элементов;

∆t_i – время испытаний.

При этом отказавшие в процессе испытаний элементы не заменяются новыми, и число работающих элементов постепенно уменьшается.

В отличие от частоты отказов, интенсивность отказов характеризует надежность объекта в данный момент времени, т. е. его локальную надежность.

Под интенсивностью отказов понимают число отказов в единицу времени, отнесенное к среднему числу элементов, безотказно работающих в данный промежуток времени. При этом отказавшие элементы не заменяются.

- интенсивность отказов:

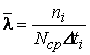,                                                     (3.9)

где  n_i – число отказов за время ∆t_i;

 – среднее число работоспособных элементов;

N_i – число элементов, работоспособных в начале рассматриваемого промежутка времени;

N_i+1 – число элементов, работоспособных в конце промежутка времени ∆t_i.

И нтенсивность отказов в течение длительной эксплуатации не остается постоянной. В начальный период времени  имеет большее значение вследствие скрытых дефектов, не обнаруженных из-за несовершенства производственного контроля и возможных нарушений правил эксплуатации при первоначальной наладке объекта. Затем значение интенсивности отказов уменьшается и остается почти постоянным в течение длительного срока. В конце срока службы λ возрастает из-за старения элементов устройства. На рис. 3.2 изображена зависимость интенсивности отказов от времени.

Среднее время безотказной работы, или средняя наработка на отказ, определится по данным испытаний, как

^,      (3.10)

где t_i – время исправной работы i-го элемента;

N – общее число испытуемых элементов.

При большом количестве элементов формула (3.10) становится слишком громоздкой. Используется другой способ вычисления среднего времени

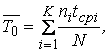                                              (3.11)

где  n_i – количество отказавших элементов в интервале времени ∆t = t_i+1 - t_i;

t_i – время в начале i-го интервала;

t_i+1 – время в конце i-го интервала;

 – среднее время в i-ом интервале;

 – число интервалов или разрядов;

t_N – время, в течение которого отказали все элементы.