
- •Расчет вероятностей при многократных испытаниях
- •Простейший поток событий
- •Законы распределения случайных величин
- •Обработка результатов измерений
- •Основные показатели надежности невосстанавливаемых (неремонтируемых) систем
- •Основные показатели надежности восстанавливаемых (ремонтируемых) систем
- •Законы распределения, используемые при оценке надежности
- •Аналитические методы расчета надежности информационных систем
- •Повышение надежности систем путем резервирования
- •Расчет надежности по статистическим данным
- •Доверительные интервалы при нормальном распределении случайной величины
- •Доверительные интервалы при экспоненциальном распределении случайной величины
- •Определение доверительных интервалов при отсутствии отказов
- •Критерии согласия. Критерий Пирсона
- •Критерий Колмогорова
- •Классификация помехоустойчивых кодов
- •Основные характеристики корректирующих кодов
- •Корректирующие коды Хемминга
- •Основные выводы использования корректирующих кодов
- •Типы отказов и сбоев при исполнении комплекса программ
- •Основные факторы, влияющие на надежность функционирования комплекса программ
- •Обеспечение надежности и повышение качества программ
- •Тестирование и испытание программ
- •Критерии надежности программных комплексов
- •Функциональная диагностическая модель
- •Построение таблицы неисправностей или матрицы состояний
- •Основные способы построения алгоритмов поиска неисправностей
ОСНОВНЫЕ ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Основные определения и термины
Возникновение отказов в информационных системах зависит от разных факторов и носит случайный характер. Поэтому для количественной оценки различных характеристик систем используются вероятностные методы.
В теории вероятностей случайной называется величина, которая в результате опыта может принять то или иное значение, предугадать которое заранее и достоверно невозможно.
Событием в теории вероятностей считается всякий факт, который в результате опыта может произойти, а может и не произойти.
Для количественного сравнения между собой событий по степени их возможности используется определенное число, которое тем больше, чем более возможно событие. Такое число называется вероятностью события.
В практике о вероятности события судят по частоте его появления. Если в n опытах событие А появилось m раз, то его частота или статистическая вероятность может быть определена соотношением
![]() .
.
Невозможным называется событие, которое заведомо не произойдет. Вероятность невозможного события равна нулю.
Достоверным называется событие, которое обязательно произойдет. Вероятность достоверного события равна единице.
Вероятность произвольного случайного события изменяется от нуля до единицы.
Если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном опыте это событие не наступит. Очень малая вероятность – это значения, заключенные между 0,01 и 0,05. Это свойство называется принципом практической невозможности маловероятных событий.
При неограниченном увеличении числа опытов статистическая вероятность сходится по вероятности к математической, т. е. частота с вероятностью сколь угодно близкой к единице, приближается к математической вероятности Р(А).
Если исходы (результаты) испытаний единственно возможны и равновозможны, математическая вероятность события А может быть вычислена по формуле:
![]() ,
,
где n – общее число равновозможных элементарных исходов испытаний;
m – число благоприятных исходов, в которых появляется событие А.
При вычислении величин m и n используется теория сочетаний.
Число сочетаний из m элементов по n вычисляется по любой из двух формул:
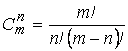 ,
(2.1)
,
(2.1)
![]() .
(2.2)
.
(2.2)
Примеры:
![]() ;
;
![]() ;
;
![]() .
.
Гипергеометрическое распределение
При решении задач контроля качества продукции используется гипергеометрическое распределение
 .
(2.3)
.
(2.3)
Из группы в n элементов, состоящих из m элементов одного типа и (n – m) элементов другого типа, берется наугад группа из r элементов. Определяется вероятность того, что среди r элементов будет k элементов первого типа.
Основные теоремы теории вероятностей
Несколько событий называют несовместными в данном опыте, если никакие два из них не могут появиться вместе.
Теорема сложения утверждает, что если события A и B несовместны, то вероятность появления одного из них, безразлично какого, равна сумме вероятностей этих событий
![]()
Следствие.
Вероятность появления одного из нескольких попарно несовместимых событий, безразлично какого, равна сумме вероятностей этих событий.
![]()
Во многих реальных ситуациях событие А может произойти вместе с одним из событий Н1, Н2, …, Нn, образующих полную группу событий. Эти события называются гипотезами.
![]()
Безусловная вероятность P(A) события А вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при этой гипотезе.
 (2.4)
(2.4)
Данная формула называется формулой полной или средней вероятности.
Пусть имеется
полная группа несовместных гипотез Н1,
Н2,
…, Нn.
Вероятности этих гипотез до опыта
известны и равны соответственно
![]() ,
,![]() …,
…,
![]() .
Произведен опыт, в результате которого
наблюдается появление некоторого
события А. Условные вероятности гипотез
после опыта определяются по формуле
Бейеса.
.
Произведен опыт, в результате которого
наблюдается появление некоторого
события А. Условные вероятности гипотез
после опыта определяются по формуле
Бейеса.
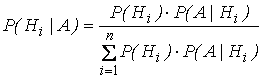 .
(2.5)
.
(2.5)
(i = 1, 2, ..., n).
Формула Бейеса позволяет переоценить вероятности гипотез после того, как становится известен результат испытания, в итоге которого появляется событие А. Если в результате испытания прибор вышел из строя, гипотезы Н1 и Н2 становятся невозможными. Необходимо выяснить и устранить причины отказа прибора.
Расчет вероятностей при многократных испытаниях
Несколько опытов называют независимыми, если вероятность того или иного исхода каждого из опытов не зависит от исходов других опытов.
Пусть вероятность появления события A во всех независимых опытах одна и та же и равна р. В таком случае, вероятность появления события A в n опытах m раз определяется по формуле Бернулли:
![]() (2.6)
(2.6)
Если число испытаний велико, а вероятность появления события Р в каждом испытании очень мала, пользуются формулой Пуассона:
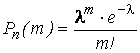 ,
(2.7)
,
(2.7)
где m – число появлений события в n испытаниях;
![]() –
среднее число
появлений события в n
испытаниях.
–
среднее число
появлений события в n
испытаниях.
Формула Пуассона именуется законом редких явлений.
Если число независимых опытов n в формуле Бернулли велико, пользуются асимптотической формулой Лапласа:
 ,
(2.8)
,
(2.8)
где
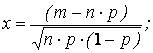
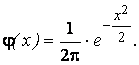
Если вероятность
p
наступления события А в каждом испытании
постоянна и отличается от 0 и 1, то
вероятность
![]() того,
что событие А появится в n
испытаниях от К1
до К2
раз, приближенно равна определенному
интегралу:
того,
что событие А появится в n
испытаниях от К1
до К2
раз, приближенно равна определенному
интегралу:
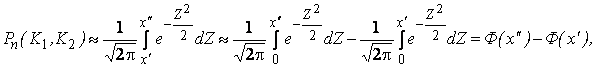 (2.9)
(2.9)
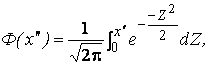

где 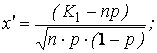
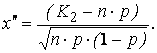
![]() и
и
![]() –
интегралы Лапласа, величины интегралов
определяются по таблице.
–
интегралы Лапласа, величины интегралов
определяются по таблице.
Простейший поток событий
Потоком событий называется последовательность событий, которые наступают в случайные моменты времени.
Простейшим (Пуассоновским) называют поток событий, обладающий свойствами стационарности, отсутствия последействия, ординарности.
Свойство стационарности состоит в том, что вероятность появления событий не зависит от выбора отсчета времени.
Свойство отсутствия последействия заключается в том, что предыстория потока не сказывается на вероятности появления события в ближайшем будущем.
Ординарность потока означает, что вероятность появления двух событий одновременно отсутствует
Интенсивностью потока называется среднее число событий, которые появляются в единицу времени.
Если интенсивность потока постоянна, то вероятность появления К событий простейшего потока за время t определяется формулой Пуассона:
 (2.10)
(2.10)
Законы распределения случайных величин
Случайные величины могут быть дискретными или непрерывными.
Дискретной называют величину m, принимающую конечное или счетное число значений.
Законом распределения дискретной случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и вероятностями их появления. Закон распределения может быть задан в табличной форме. Например:
X |
2 |
9 |
7 |
6 |
p |
0.5 |
0.2 |
0.2 |
0.1 |
Непрерывной является величина, которая может принимать любое значение из некоторого конечного промежутка. Число возможных значений непрерывной случайной величины n бесконечно. Вероятность того, что непрерывная величина примет определенное значение, равна нулю.
![]() ,
так как n
.
,
так как n
.
Поэтому интегральной функцией распределения называется функция вида
![]()
Функция распределения существует как для дискретных, так и для непрерывных величин и характеризует вероятность события Х < x, где х – текущая переменная.
Свойства функции распределения.
1. F(x) – возрастающая функция.
2.
![]() .
.
3. Если возможные значения случайной величины принадлежат интервалу [a, b], то F(x) = 0 при x a, F(x) = 1 при x b.
Производная интегральной функции называется дифференциальной функцией распределения, плотностью распределения или плотностью вероятностей. Плотность распределения существует только для непрерывных случайных величин.
Каждый закон распределения представляет собой некоторую функцию, которая полностью описывает случайную величину с вероятностной точки зрения.
Однако на практике достаточно указать параметры, характеризующие в сжатой форме случайную величину. Это математическое ожидание и дисперсия. Для дискретной величины математическое ожидание – это сумма произведений всех возможных значений случайной величины на вероятность этих значений.
 ,
(2.11)
,
(2.11)
для непрерывной величины
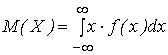 ,
(2.12)
,
(2.12)
где
![]() –
плотность распределения величины х.
–
плотность распределения величины х.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
![]() .
(2.13)
.
(2.13)
Пусть случайная величина задана законом распределения
Х |
x1 |
x2 |
…. |
xn |
p |
p1 |
p2 |
…. |
pn |
По определению дисперсии
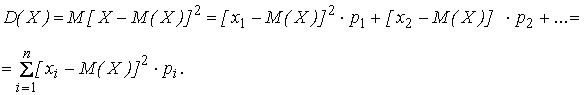 (2.14)
(2.14)
Для непрерывной случайной величины
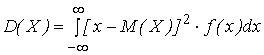 .
(2.15)
.
(2.15)
Среднеквадратичное отклонение случайной величины
![]() .
(2.16)
.
(2.16)
На практике приходится определять численные характеристики случайной величины по ограниченному объему статистических данных.
Статистическое математическое ожидание (среднее значение):
 ,
(2.17)
,
(2.17)
где n – количество экспериментальных данных.
Статистическая дисперсия:
 .
(2.18)
.
(2.18)
Возможно получить еще одну формулу для вычисления дисперсии:
-
(2.19)

Еще знаменитый
астроном-наблюдатель Тихо Браге (1546 –
1601) обратил внимание на то, что точность
измерений значительно повышается, если
произвести несколько измерений и взять
из них среднее арифметическое. Этот
эмпирический факт объясняется теоремой
Чебышева. Теорема Чебышева утверждает:
если x1,
x2,
… , xn
– попарно независимые случайные
величины, имеющие одно и то же математическое
ожидание М и если дисперсии этих величин
равномерно ограничены (не превышают
постоянного числа С), то, как ни мало
> 0,
вероятность неравенства
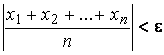 будет
сколь угодно близка к единице, если
число случайных величин достаточно
велико.
будет
сколь угодно близка к единице, если
число случайных величин достаточно
велико.
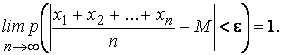
Сущность теоремы Чебышева состоит в том, что при достаточно больших количествах измерений их среднее арифметическое мало отличается от истинного значения измеряемой величины. Истинное значение равно математическому ожиданию величины.
На теореме Чебышева основан выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности исследуемых объектов. Например, о качестве зерна судят по небольшой его пробе. Число наудачу отобранных зерен мало по сравнению со всей массой зерна, но само по себе велико.
