11.3.3. Методы Рунге-Кутта

Чтобы удержать в ряде Тейлора (11.3) член n-го порядка, необходимо вычислить n-ю производную зависимой переменной. При использовании модифицированного метода Эйлера для получения второй производной в конечно-разностной форме достаточно знать наклоны кривой на концах рассматриваемого интервала. Чтобы вычислить третью производную в конечно-разностном виде, необходимо иметь значения второй производной по меньшей мере в двух точках. Для этого необхо­димо дополнительно определить наклон кривой в некоторой промежуточ­ной точке интервала h, т. е. между точками x_n и x_{n + 1}. Очевидно, чем выше по­рядок вычисляемой производной, тем больше дополнительных вычислений потребуется внутри интервала. Метод Рунге-Кутта дает набор формул для расчета координат внутренних точек, требуемых для реализации этой идеи. Так как существует несколько способов определения распо­ложения внутренних точек и нахождения в них значения производных, то метод Рунге-Кутта в сущности объединяет целое семейство методов ре­шения дифференциальных уравнений первого порядка. Наиболее распрост­раненным из них является метод, при котором удерживаются все члены, включая h⁴. Это метод четвертого порядка точности, для которого ошибка на шаге имеет порядок h⁵. Расчеты при использовании этого классического метода производятся по формуле:

, (11.10)

где

, ,

, . (11.11)

Метод Эйлера и его модификация по сути дела являются методами Рунге-Кутта первого и второго порядка соответственно. По сравнению с методом Эйлера и его модификацией метод Рунге-Кутта имеет важное преимущество, так как обеспечивает более высокую точность, которая оправдывает дополнительное увеличение объема вычислений. Более высо­кая точность метода Рунге-Кутта часто позволяет увеличить шаг интег­рирования h. Допустимая погрешность на шаге определяет его макси­мальную величину. Чтобы обеспечить высокую эффективность вычисли­тельного процесса, величину h следует выбирать именно из соображений максимальной допустимой ошибки на шаге. Такой выбор часто осущест­вляется автоматически и включается как составная часть в алгоритм, построенный по методу Рунге-Кутта.

Относительную точность одношаговых методов продемонстрируем на примере расчета переходного процесса для схемы, приведенной на рис. 1.1.

Задача сводиться к решению дифференциального уравнения (1.8):

. (11.12)

Разделив левую и правую части на L получим:

. (11.13)

(11.14)

Это линейное уравнение имеет точное аналитическое решение, которое описывает переходной процесс:

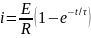, (11.15)

которое позволит сравнить относительную точность, обеспечиваемую

разными методами.

Пусть напряжение источника ЭДС E = 100В, R = 10 Ом, L = 0,1 Гн, τ = L/R – постоянная времени цепи, τ = 0,01 с, при начальном условии i(0) = 0, на временном интервале 0 < t < 0,01 c и шаге Δt = 0,001 c.

Результаты расчета представлены в таблице 11.1, из которой хорошо видны преимущества метода Рунге-Кутта по сравнению с обычным и модифицированным методами Эйлера.