- •5. Нессиметричные аварийные режимы систем электроснабжения
- •5.1. Поперечная несимметрия сэс в аварийных режимах
- •5.2. Междуфазное короткое замыкание (двухфазное кз)
- •5.3. Учёт переходного сопротивления в месте короткого замыкания
- •5.4. Однофазное короткое замыкание
- •5.5 Соотношения между токами несимметричных коротких замыканий и трехфазного короткого замыкания
5.3. Учёт переходного сопротивления в месте короткого замыкания
При расчетах КЗ в распределительных сетях особое значение имеет учет переходных сопротивлений и контактных соединений в месте КЗ.
Обычно в этом месте образуется некоторое переходное сопротивление, состоящее из сопротивления возникшей электрической дуги и сопротивлений прочих элементов пути тока от одной фазы к другой. Электрическая дуга возникает либо с самого начала повреждения, как, например при перекрытии или пробое изоляции, либо через некоторое время, когда перегорит элемент, вызвавший КЗ. При КЗ между фазами переходное сопротивление определяется главным образом сопротивлением электрической дуги.
В ряде случаев переходные сопротивления столь малы, что практически ими можно пренебречь. Естественно, что при прочих равных условиях ток при таком КЗ больше, чем при наличии переходного сопротивления. Поэтому, когда требуется найти возможные наибольшие значения токов, исходят из наиболее тяжелых условий, считая, что в месте КЗ никаких переходных сопротивлений нет. Рассмотрим учёт переходного сопротивления при междуфазном КЗ, предполагая, что переходное сопротивление в основном определяется сопротивлением электрической дуги, которое в первом приближении можно считать активным сопротивлением rд.
Пусть КЗ между фазами B и C (рис. 5.5) произошло через сопротивление дуги rд. Его можно представить как глухое междуфазное КЗ на ответвлении, фазы которого имеют одинаковые сопротивления 0,5rд. Таким приемом несимметричный участок трёхфазной цепи приведен к симметричному, что облегчает применение метода симметричных составляющих. Введение сопротивления 0,5rд в фазу А не меняет условий рассматриваемого КЗ, поскольку на данном участке ток отсутствует.
Считая остальную часть схемы чисто индуктивной, по аналогии с (5.13) запишем ток прямой последовательности в месте КЗ в виде:
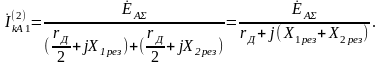 (5.23)
(5.23)
Напряжение обратной последовательности за сопротивлением дуги rд с учетом (5.11) и (5.20)
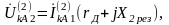 (5.24)
(5.24)
а
напряжение прямой последовательности
в этой же точке определяется уравнением
(5.12), т.е.
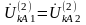 .
.
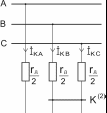
Рис. 5.5
5.4. Однофазное короткое замыкание
На рис. 5.6 показана схема ответвлений в точке однофазного КЗ. Граничными условиями для однофазного КЗ являются соотношения:
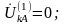
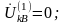
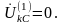 (5.25)
(5.25)
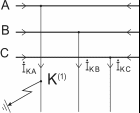
Рис. 5.6
Вычитая
из второго уравнения третье в системе
(5.2) и учитывая ГУ (5.25), получаем
 и в итоге
и в итоге
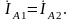 (5.26)
(5.26)
Складывая
второе и третье уравнения (5.2) с учетом
(5.25) и (5.26), получаем:
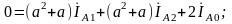
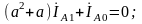
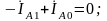 в итоге
в итоге
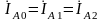 ;
(5.27)
;
(5.27)
С учетом (5.27) переписываем уравнения (5.1):
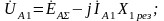
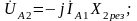
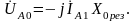 (5.1′)
(5.1′)
Из
(5.25) следует
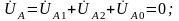
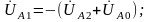 с учетом (5.1′)
с учетом (5.1′)
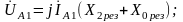 из первого уравнения (5.1′) получаем:
из первого уравнения (5.1′) получаем:
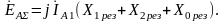
Отсюда определяем симметричную составляющую прямой последовательности тока фазы А:
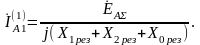 (5.28)
(5.28)
Ток фазы А в аварийном режиме (см. рис. 5.6) с учетом (5.27):
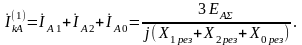 (5.29)
(5.29)
Коэффициент взаимосвязи токов в случае однофазного КЗ:
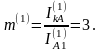 (5.30)
(5.30)
Для начального момента времени (t = 0) переходного процесса абсолютное значение тока однофазного КЗ (т.е. сверхпереходный ток) определяем по аналогии с (5.29):
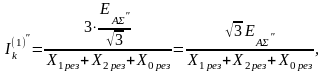 (5.31)
(5.31)
где
 фазная сверхпереходная результирующая
ЭДС.
фазная сверхпереходная результирующая
ЭДС.
При питании от электроэнергетической системы (ЭЭС) со средним линейным, номинальным напряжением UСР:
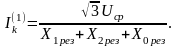 (5.32)
(5.32)
Действительные напряжения в месте КЗ находим на основе уравнений (5.1′), (5.3), (5.25)
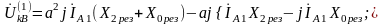 (5.33)
(5.33)
 (5.34)
(5.34)
Построим
векторные диаграммы токов. Построение
проводим в следующем порядке. В
произвольном направлении (например,
направо горизонтально) откладываем
вектор
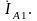 Учитывая равенство (5.27), так же откладываем
векторы
и
Учитывая равенство (5.27), так же откладываем
векторы
и
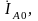 а затем и вектор
а затем и вектор
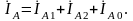
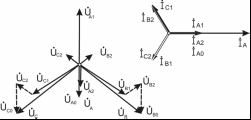
Рис. 5.7
К
вектору
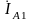 достраиваем
векторы
и
достраиваем
векторы
и
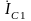 ,
а к вектору
–
векторы
и
,
а к вектору
–
векторы
и
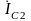 .
Векторы
.
Векторы
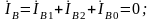
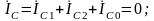 т.к.
т.к.
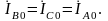
Далее
строим векторы
и
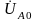 на основе формул (5.1′), затем достраиваем
на основе формул (5.1′), затем достраиваем
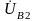 и
и
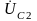 .
Вектор
.
Вектор
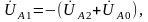 достраиваем к нему
достраиваем к нему
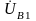 и
и
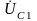 .
В
итоге определяем векторы фазных
напряжений
.
В
итоге определяем векторы фазных
напряжений
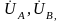 и
и
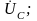
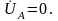
Допустим
теперь, что фаза А замкнулась на землю
через сопротивление дуги
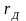 (рис.
5.8). Чтобы сохранить симметрию
рассматриваемого участка трёхфазной
цепи, принимаем, что такие же сопротивления
есть в двух других фазах. Это допустимо,
так как не нарушает граничных условий:
(рис.
5.8). Чтобы сохранить симметрию
рассматриваемого участка трёхфазной
цепи, принимаем, что такие же сопротивления
есть в двух других фазах. Это допустимо,
так как не нарушает граничных условий:
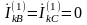 (как
и в схеме рис. 5.6).
(как
и в схеме рис. 5.6).
При
наличии дуги результирующее сопротивление
каждой последовательности увеличивается
на
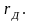 Следовательно, по аналогии с (5.28) можно
найти в месте КЗ:
Следовательно, по аналогии с (5.28) можно
найти в месте КЗ:
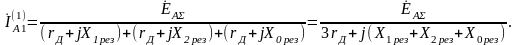 Напряжение
прямой последовательности
за сопротивлением (точка
Напряжение
прямой последовательности
за сопротивлением (точка
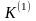 ):
):
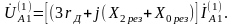 (5.
36)
(5.
36)
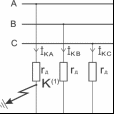
Рис. 5.8
Если сравнить формулы для определения симметричной составляющей прямой последовательности тока фазы А, то можно сделать следующее обобщение: формулы (5.28), (5.13) и (5.5) можно записать в виде
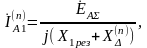 (5.37)
(5.37)
где
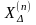 -
добавочное сопротивление в КЗ – ветви
в случае КЗ типа (n).
-
добавочное сопротивление в КЗ – ветви
в случае КЗ типа (n).
При n
= 3 (трёхфазное КЗ)
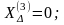 при n
= 2
при n
= 2
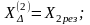 при n
= 1
при n
= 1