7. Циркуляция вектора в для магнитного поля в вакууме.

Введем, аналогично циркуляции вектора напряженности электростатического поля, циркуляцию вектора магнитной индукции. Циркуляцией вектора В по заданному замкнутому контуру называется интеграл где dl — вектор элементарной длины контура, который направлен вдоль обхода контура, B_l=Bcosα — составляющая вектора В в направлении касательной к контуру (с учетом выбора направления обхода контура), α — угол между векторами В и dl. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной μ₀ на алгебраическую сумму токов, охватываемых этим контуром: (1) где n — число проводников с токами, которые охватываются контуром L любой формы. Каждый ток в уравнении (1) учитывается столько раз, сколько раз он охватывается контуром. Ток считается положительным, если его направление образует с направлением обхода по контуру правовинтовую систему; отрицательным считается ток противоположного направления.

8. Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля

Магни́тный пото́к — поток как интеграл вектора магнитной индукции через конечную поверхность . Определяется через интеграл по поверхности

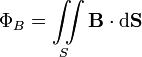при этом векторный элемент площади поверхности определяется как

где — единичный вектор, нормальный к поверхности.

Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:

где α — угол между вектором магнитной индукции и нормалью к плоскости площади.

Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру:

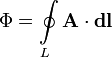
В соответствии с теоремой Гаусса для магнитной индукции поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

Или, в дифференциальной форме — дивергенция магнитного поля равна нулю:

Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.

9. Магнитные элементы электронов и атомов

Все вещества (твердые, жидкие, газ, плазма) взаимодействуют с внешним электромагнитным полем. Это значит, изолированные атомы обладают магнитными свойствами. Этот раздел и посвящен изучению магнитных свойств.

Электрон, вращающийся по орбите ядра атома, эквивалентен контуру с током. Такой контур с током должен обладать магнитным моментом и, следовательно, должен вести себя в магнитном поле как подобно магнитному диполю. Определим орбитальный момент электрона: магнитный момент контура с током I равен

10. Диамагнетики и парамагнетики. Намагниченность, магнитное поле в веществе.

Диамагне́тики — вещества, намагничивающиеся против направления внешнего магнитного поля. В отсутствие внешнего магнитного поля диамагнетики немагнитны. Под действием внешнего магнитного поля каждый атом диамагнетика приобретает магнитный момент I (а каждая единица объёма — намагниченность M), пропорциональный магнитной индукции B и направленный навстречу полю. Поэтому магнитная восприимчивость = M/H у диамагнетиков всегда отрицательна. По абсолютной величине диамагнитная восприимчивость мала и слабо зависит как от напряжённости магнитного поля, так и от температуры.

Парамагнетики — вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля (J↑↑H) и имеют положительную магнитную восприимчивость. Парамагнетики относятся к слабомагнитным веществам, магнитная проницаемость незначительно отличается от единицы .

Намагниченность — характеристика магнитного состояния макроскопического физического тела. Обозначается обычно М или J. Намагниченность равна отношению магнитного момента тела к его объёму.

Намагниченность тел зависит от внешнего магнитного поля и температуры. У ферромагнетиков зависимость J от напряжённости внешнего поля Н выражается кривой намагничивания (см. Намагничивания кривые, Гистерезис). В изотропных веществах направление J совпадает с направлением Н, в анизотропных (см. Магнитная анизотропия) направления J и Н в общем случае различны.

В общем случае описание влияния вещества на магнитное поле является очень сложной математическое задачей. Магнитное поле приводит к намагничиванию вещества, то есть вектор намагниченности вещества зависит от индукции магнитного поля, действующего на вещество J ⃗ =G(B ⃗ ) Чрезвычайная сложность этой связи обусловлена целым рядом причин:

1. В данном выражении намагниченность выделенного объема вещества зависит не только от магнитной индукции не только внешнего поля B ⃗ 0, которое может быть известно, но и поля B ⃗ ′, возникающего благодаря намагничиванию других частей вещества, которое само подлежит определению.

2. Связь между намагниченностью и индукцией поля часто бывает нелинейной, что связано с эффектами насыщения, о которых мы поговорим чуть позже.

3. Многие вещества обладают магнитной анизотропией^[1], то есть величина намагниченности может зависеть от направления, поэтому векторы намагниченности и индукции поля в общем случае не параллельны.

4. Рассматриваемая связь может быть не функциональной, так в ферромагнетиках намагниченность определяется полем не только в данный момент времени, но и «предысторией», то есть вещество частично «запоминает» какое поле действовало раньше. Подобный эффект называется магнитным гистерезисом.

Для расчета поля в присутствии магнетиков, необходимо уметь рассчитывать индукцию поля при заданном распределении намагниченности вещества, то есть B ⃗ ′ =F(J ⃗ ). Во многих случаях эта задача может быть решена (что тоже не просто) с помощью закона Био-Савара и принципа суперпозиции.