
- •Введение
- •Раздел 1 основы проектирования механизмов
- •Тема 1.1 Основы расчета деталей машин
- •Тема 1.2 Критерии работоспособности деталей машин
- •Раздел 2 механические передачи
- •Тема 2.1 Общие сведения о передачах
- •Тема 2.2 Фрикционные передачи
- •Тема 2.3 Зубчатые передачи
- •Тема 2.4 Передача винт-гайка
- •Применение передач винт-гайка
- •Разновидности винтов в передаче винт-гайка
- •Тема 2.5 Червячные передачи
- •Тема 2.6 Редукторы
- •Общие сведения о редукторах
- •Конструкция редуктора
- •Смазка и смазочные материалы
- •Мотор-редуктор
- •Тема 2.7 Ременные передачи
- •Конструктивные типы ремней
- •Устройства для натяжения ремня
- •Основные геометрические соотношения в ременной передаче
- •Упругое скольжение ремня
- •Силы, действующие в ременной передаче
- •Коэффициент тяги и кривые скольжения ремня
- •Напряжения в ремне и их круговая эпюра
- •Расчет ременных передач до тяговой способности
- •Тема 2.8 Цепные передачи
- •Силы, действующие в цепной передаче
- •Расчет (подбор) цепи
- •Тема 2.9 Валы и оси
- •Расчет валов на прочность
- •Предварительный расчет валов
- •Уточненный расчет валов
- •Расчет валов на жесткость
- •Тема 3.10 Подшипники скольжения
- •Основы гидродинамической теории смазки
- •Смазочные материалы
- •Антифрикционные материалы
- •Конструктивные типы подшипников скольжения
- •Условный расчет подшипников скольжения
- •Тема 2.11 Подшипники качения
- •Тема 2.12 Муфты
- •Классификация и назначение муфт
- •Расчет дисковой фрикционной муфты
- •Раздел 3 соединения деталей машин
- •Тема 3.1 Заклепочные и штифтовые соединения
- •Тема 3.2 Сварные и клеевые соединения
- •Применение различных видов сварки
- •Типы сварных швов и их расчет
- •Расчет швов:
- •Тема 3.3 Соединения с натягом
- •Тема 3.4 Резьбовые соединения
- •Типы резьб и их применение
- •Элементы крепежных соединений
- •Определение кпд резьбы
- •Средства против самоотвинчивания винтов и гаек
- •Материал винтовых соединений
- •Расчет винтовых соединений
- •Резьбовые соединения, работающие при циклических нагрузках
- •Тема 3.5 Шпоночные соединения
- •Расчет ненапряженных шпоночных соединений
- •Тема 3.6 Шлицевые соединения
- •Расчет шлицевых соединений
- •Список литературы
Тема 3.4 Резьбовые соединения
Классификация резьб; достоинства и недостатки резьбовых соединений; геометрические параметры резьбы; основные типы резьб; силовые соотношения в винтовой паре; расчет резьбовых соединений на прочность.
Все резьбы стандартизированы в мировом масштабе, то есть резьбы национальных стандартов соответствующих типов взаимозаменяемы.
Типы резьб и их применение
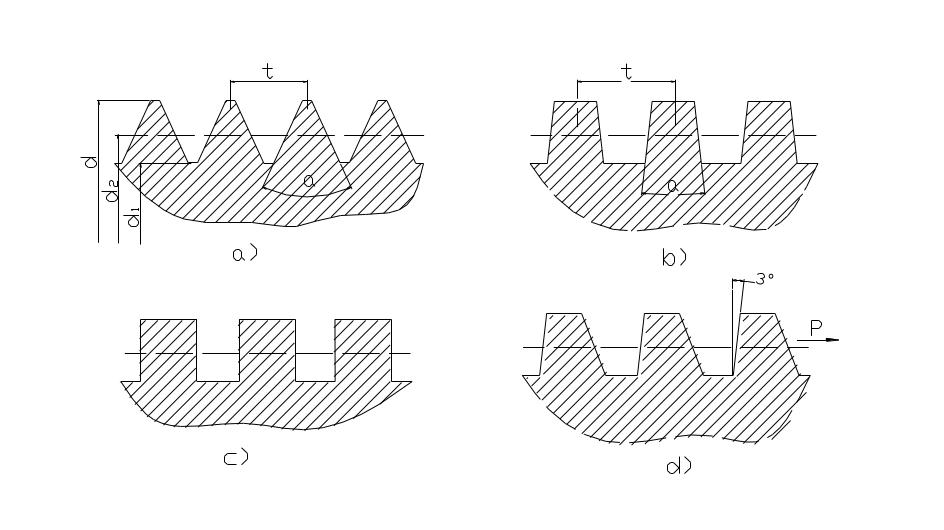
Рис. 3.4.1
По профилю резьбы разделяются на следующие типы:
а) треугольная. Основной тип крепежной резьбы. Метрическая резьба имеет угол = 60°, дюймовая - = 55°;
б) прямоугольная;
в) трапецеидальная;
г) упорная.
Резьбы типа (б), (в), (г) называются силовыми и применяются для тех винтовых соединений, в которых желательно иметь меньшие потери на трение (например, в домкратах, натяжных устройствах, подъемниках, винтовых прессах, ходовых винтах).
Прямоугольная резьба, вследствие технологических трудностей ее изготовления, применяется крайне редко и обычно заменяется резьбами типа (в) и (г). Резьба (г), как показано на рисунке, применяется только при одностороннем действии основных нагрузок; при обратном приложении нагрузки потери на трение возрастают. В некоторых случаях применяется также резьба круглого профиля (там, где имеется опасность повреждения острых кромок, например, в пожарном оборудовании, в цоколях электрических ламп).
По шагу резьбы разделяются на основные и мелкие. Мелкие резьбы для тех же диаметров имеют меньший шаг того же профиля, что и в основной резьбе. Применение мелких резьб меньше ослабляет сечение деталей и благодаря меньшему углу спирали нарезки лучше предохраняет соединение против самоотвинчивания.
Для диаметров свыше 20 мм уже обычно применяются мелкие резьбы.
Пример обозначения резьбы:
М 16 х 2 - основная; М 16 х 1,5 - мелкая.
Здесь: М - метрическая; 16 - номинальный (наружной) диаметр резьбы в мм; 2 и 1,5 - шаг резьбы в мм.
По числу заходов нарезки
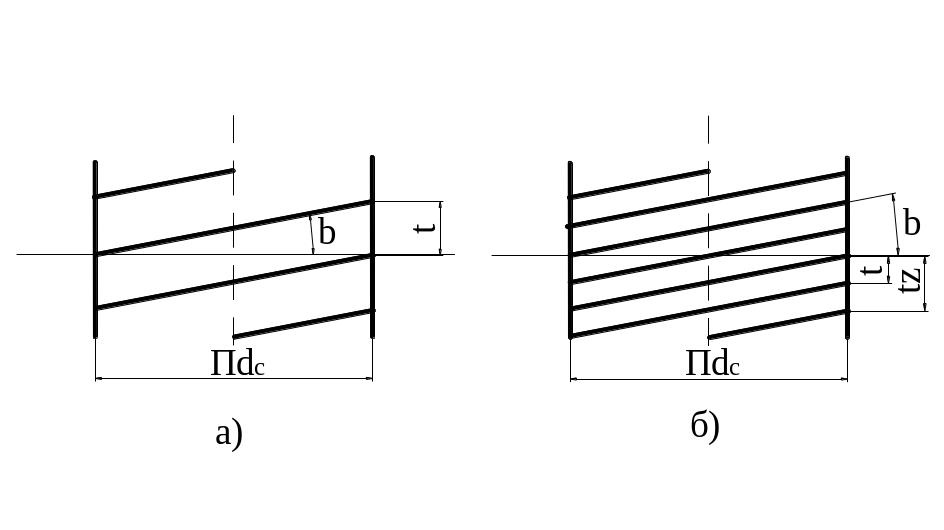
Рис. 3.4.2
Однозаходные (рис. 3.4.2 a) применяются для крепежных деталей.
Многозаходные (рис.3.4.2 б) - обычно для силовых соединений.
Цилиндрические и конусные резьбы
Рис. 3.4.3
Конусные резьбы (рис.3.4.3) применяется там, где необходимо герметически плотное соединение (пробки, трубы, наконечники арматуры). Применяются конусные резьбы как метрической, так и дюймовой системы измерения.
Для возможности свертывания конических резьб с цилиндрическими, биссектриса угла профиля конусной резьбы по ГОСТ перпендикулярна оси.
Метрические и дюймовые резьбы
В дюймовых резьбах шаг определяется числом ниток резьбы на дюйм.
Элементы крепежных соединений
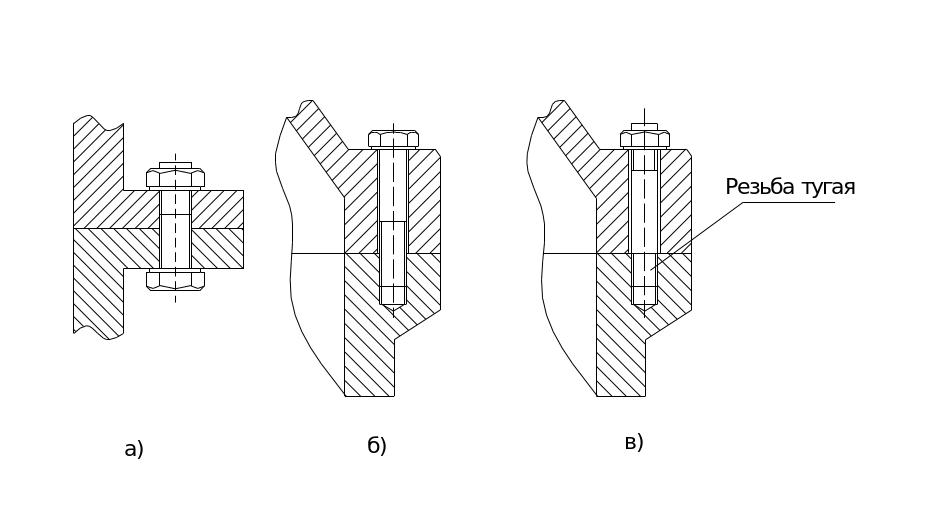
Рис. 3.4.4
Болт (рис. 3.4.4 a) требует для размещения гайки много места что увеличивает габариты и вес конструкции. Зато, при обрыве он легко заменяется.
Винт (рис.3.4.4 6) может иметь головку разной формы, в частности и шестигранную. Винт ввертывается в корпус и поэтому требует мало места для размещения, что сокращает размеры и вес конструкции. Однако, при сборке, резьба в корпусе (в особенности чугунном или алюминиевом) может быть повреждена. При обрыве трудно извлечь оставшуюся в резьбе часть винта.
Шпилька также ввертывается в корпус, для чего имеет с этой стороны тугую нарезку. При разборке свинчивается только гайка и тугая резьба в корпусе не повреждается. Шпильки рекомендуется применять при чугунных или алюминиевых корпусах. Силовые зависимости в резьбовом соединении
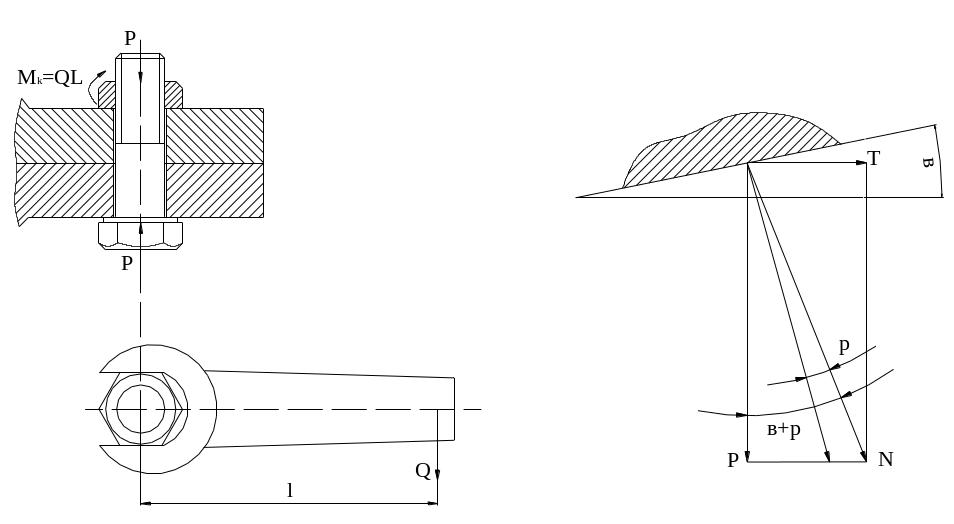
Рис. 3.4.5
Зависимость между осевой силой и крутящим моментом на оси винта иди гайки при завинчивании
Dc - средний диаметр трения по торцу головки или гайки;
dc - средний диаметр резьбы;
Mk - крутящий момент на оси ;
P - осевое усилие;
Т - окружное усилие по среднему диаметру резьбы;
N - нормальное усилие взаимодействия между винтом и гайкой, вектор которого смещен на угол трения ;
f - коэффициент трения в торце;
f1 - коэффициент трения в резьбе.
tg = f1
При завинчивании возникают моменты трения в резьбе и на торце:
Mk = Mрез + Mгор
Mрез
=
T![]() =
P
tg(+)
=
P
tg(+)
Mгор
=
Pf![]()
Mk = P tg(+) + Pf
Mk = P [tg(+) + f ]
