8.3. Кручение с изгибом

Вид нагружения, при котором брус подвергается одновременно действию скручивающих и изгибающих моментов, называется изгибом с кручением.

При расчете воспользуемся принципом независимости действия сил. Определим напряжения по отдельности при изгибе и кручении (рис. 8.8).

При изгибе в поперечном сечении возникают нормальные напряжения, достигающие максимального значения в крайних волокнах

.

При кручении в поперечном сечении возникают касательные напряжения, достигающие наибольшего значения в точках сечения у поверхности вала

.

Нормальные и касательные напряжения одновременно достигают наибольшего значения в точках С и В сечения вала (рис. 8.9). Рассмотрим напряженное состояние в точке С (рис. 8.10). Видно, что элементарный параллелепипед, выделенный вокруг точки С, находится при плоском напряженном состоянии.

Поэтому для проверки прочности применим одну из гипотез прочности.

Условие прочности по третьей гипотезе прочности (гипотезе наибольших касательных напряжений)

.

Учитывая, что , , получим условие прочности вала

. (8.6)

Если изгиб вала происходит в двух плоскостях, то условие прочности будет

.

Используя четвертую (энергетическую) гипотезу прочности

,

после подстановки s и t получим

. (8.7)

Вопросы для самопроверки

1.   Какой изгиб называется косым?

2.    Сочетанием каких видов изгиба является косой изгиб?

3.   По каким формулам определяются нормальные напряжения в поперечных сечениях балки при косом изгибе?

4.  Как находится положение нейтральной оси при косом изгибе?

5.  Как определяются опасные точки в сечении при косом изгибе?

6.  Как определяются перемещения точек оси балки при косом изгибе?

7. Какой вид сложного сопротивления называется внецентренным растяжением (или сжатием)?

8. По каким формулам определяются нормальные напряжения в поперечных сечениях стержня при внецентренном растяжении и сжатии? Какой вид имеет эпюра этих напряжений?

9. Как определяется положение нейтральной оси при внецентренном растяжении и сжатии? Запишите соответствующие формулы.

10. Какие напряжения возникают в поперечном сечении бруса при изгибе с кручением?

11. Как находятся опасные сечения бруса круглого сечения при изгибе с кручением?

12. Какие точки круглого поперечного сечения являются опасными при изгибе с кручением?

13. Какое напряженное состояние возникает в этих точках?

Лекция 9.Устойчивость сжатых стержней

Вопросы лекции:

1. Понятие об устойчивости. Задача Эйлера.

2. Влияние способов закрепления концов стержня на критическую силу.

3. Пределы применимости формулы Эйлера.

4. Расчет стержней на устойчивость по коэффициенту снижения допускаемых напряжений.

9.1. Понятие об устойчивости. Задача Эйлера

Из теоретической механики известно, что равновесие абсолютно твердого тела может быть устойчивым (рис. 9.1а) безразличным (рис. 9.1б) и неустойчивым (рис 9.1в и г).

а б в г

Рис. 9.1

Равновесное состояние деформируемой системы, например стержня, также может быть устойчивым (рис. 9.2а), безразличным (критическим) (рис. 9.2б) и неустойчивым (рис. 9.2в).

а б в

Рис. 9.2

Строгое определение устойчивости по теореме Пуанкаре звучит так.

П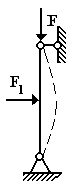 усть идеально прямой стержень нагружен строго центральной продольной силой (рис. 9.3). При таких предположениях прямолинейная форма стержня всегда будет являться возможной формой равновесия. Об устойчивости этой формы равновесия стержня можно судить по реакции ее на поперечную нагрузку F₁. При отсутствии силы F малая сила F₁ вызывает малый прогиб стержня. При небольшой силе F положение стержня не изменится, а равновесие его сохранится устойчивым.

Равновесие стержня устойчиво, если, задавшись любой вели-чиной прогиба f  0, всегда можно указать такую конечную величину возмущения , что при величина прогиба ни в одной точке системы не достигнет величины f, т.е. будет   f.

Нагрузка, при которой начальная (исходная) форма равновесия стержня перестает быть устойчивой, называется критической и обозначается F_кр. Приложение к стержню силы или

Рис. 9.3 вызывает его продольный изгиб.

Явление перехода системы от одного равновесного состояния к другому равновесному состоянию, называется потерей устойчивости системы.

В некоторых случаях при потере устойчивости система, переходя в новое устойчивое равновесное состояние, продолжает выполнять свои функции. Однако в подавляющем большинстве случаев потеря устойчивости системы сопровождается возникновением больших перемещений, пластических деформаций или ее полным разрушением. Поэтому сохранение исходного (расчетного) равновесного состояния системы является важной задачей и одной из основных проблем сопротивления материалов.

Но потеря устойчивости упругого равновесия возможна и при других видах деформаций. Так, при прямом изгибе балок направление прогиба балки может существенно отклониться от линии действия нагрузки (рис. 9.4 б), и, наконец, при действии внутреннего давления на цилиндрическую оболочку ее деформации в некоторый момент перестают быть осесимметричными, оболочка искривляется и принимает некоторую новую форму (рис. 9.4 в).

а б в

Разрушение от сжимающих критических нагрузок наступает внезапно при отсутствии внешних признаков приближающей потери устойчивости. Практически мгновенно происходит изменение характера нагружения, приводящего к разрушению конструкции. Так, например, продольно сжатый прямолинейный стержень принимает изгибную форму равновесия. Поэтому явление потери устойчивости сжимаемого бруса называют также продольным изгибом бруса.

Впервые поставил и решил задачу о потере устойчивости прямолинейной формы сжатого стержня академик Петербургской академии наук Леонард Эйлер (1707 – 1783) в 1744 г.

Рассмотрим решение задачи об устойчивости сжатого стержня. Пусть стержень, оба конца которого закреплены шарнирно, сжат силой F_кр (рис. 9.5). Стержень искривился так, что в сечении x прогиб составил z.

Приближенное дифференциальное уравнение изогнутой оси балки имеет вид: .

Рис. 9.5

 Изгибающий момент в сечении x в изогнутом состоянии равен моменту силы F_кр, но обратного направления, а следовательно, и знака .

Тогда дифференциальное уравнение изогнутой оси балки в направлении минимальной жесткости будет

. (9.1)

Обозначая , из (9.1) получим линейное дифференциальное уравнение второго порядка относительно прогиба z .

Его общее решение имеет вид: , где С и D – постоянные интегрирования, определяемые из условий на опорах.

На опорах стержня прогиб равен нулю, т.е. 1) при x = 0, z = 0; 2) при x = l, z = 0. Подставляя первое условие в уравнение прогибов, получим С = 0, из второго условия получим .

Последнее соотношение справедливо при , где n – любое целое число. Тогда имеем и с учетом принятого ранее обозначения, получим

.

Минимальное действительное значение критической силы получится при n=1:

. (9.2)

Это и есть формула Эйлера для критической силы.

Прогиб стержня с шарнирным закреплением концов происходит по синусоиде с одной полуволной

.