7.4. Пример расчета

Для стальной балки, изображенной на рис. 7.3, определить методом начальных параметров углы поворота сечения и прогиб в точке D. Модуль упругости Е = 210⁸ кН/м². Поперечное сечение балки  квадратное со стороной a = 0,2 м.

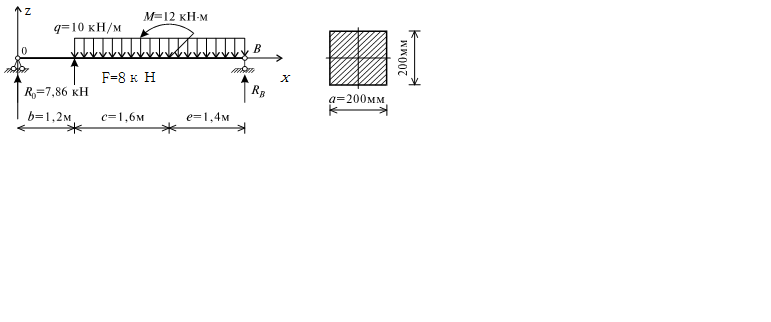
Рис. 7.3

Решение

1. Определение опорных реакций балки (рис. 7.3).

M₀ =0,    R_B (b + c + e)  q(c + e)b + 0,5(c + e) + M + P b = 0,

кН;

M_B =0,    R₀ (b + c + e)  0,5q(c + e)²  M + P(c + e) = 0,

кН.

Для проверки правильности определения опорных реакций составим уравнение равновесия сил по оси z:

z =0; R₀ + R_B + F  q (c + e) = 7,86 + 14,14 + 8  103 = 30  30 = 0.

Реакции найдены верно.

2. Применение метода начальных параметров.

Используя метод начальных параметров, для рассматриваемой балки запишем:

Из условий закрепления балки при x = 0 имеем: z₀ = 0; М₀=0.

Подставляя числовые значения, получим:

.

В данном выражении неизвестно ₀. Из условия закрепления балки при x = b + c + e имеем, что z = 0. Вычисляя прогиб на правом конце балки и приравнивая его к нулю, получим уравнение для определения ₀:

.

Отсюда E I ₀ = 20,84 кНм². Теперь выражение для определения прогибов будет иметь вид:

.

Соответственно выражение для определения углов поворота будет:

.

С помощью этих выражений определяем z_D и _D:

кHм³.

кНм².

Вычисляем жесткость сечения (Е = 210⁸ кН/м²):

кНм².

Тогда окончательно

м.

рад.

Перемещение точки D происходит вниз, а сечение поворачивается по часовой стрелке.

Вопросы для самопроверки

1. Какие перемещения получают поперечные сечения балок при прямом изгибе?

2. Запишите основное дифференциальное уравнение изогнутой оси балки.

3. Что называется жесткостью сечения при изгибе?

4. Как из основного (приближенного) дифференциального уравнения изогнутой оси балки получаются выражения углов поворота и прогибов ее сечений?

5. Из каких условий определяются постоянные интегрирования, входящие в уравнение углов поворота и прогибов сечений балки?

6. Запишите универсальное уравнение метода начальных параметров.

7. Перечислите основные параметры для использования метода начальных параметров.

8. Что надо сделать, если распределенная нагрузка не доходит до правого конца балки?

Лекция 8. Сложное сопротивление

Вопросы лекции:

1. Косой изгиб.

2. Внецентренное растяжение (сжатие).

3. Кручение с изгибом.

Ранее были рассмотрены виды нагружения, при которых в сечениях элементов конструкций возникал только один внутренний силовой фактор: нормальная сила N – при растяжении, изгибающий момент М_y – при чистом изгибе, крутящий момент М_к – при кручении. Исключением явился лишь случай плоского изгиба (поперечный изгиб), при котором в поперечных сечениях стержня возникают одновременно два внутренних силовых фактора: изгибающий момент и поперечная сила. Но и в этом случае при расчетах на прочность и жесткость, как правило, учитывается только изгибающий момент. Эти виды нагружения – растяжение, изгиб и кручение являются простыми.

Однако на практике часто встречаются и случаи сложного сопротивления, когда в поперечных сечениях стержня одновременно действует несколько внутренних силовых факторов, учитываемых при расчете на прочность (продольная сила и крутящий момент, крутящий и изгибающий моменты и т. п.).

Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.

Наиболее часто в расчетной практике встречаются следующие виды сложного сопротивления:

– косой изгиб;

– внецентренное растяжение;

– кручение с изгибом.

При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения, действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.