Задание 6

Пусть R₁ и R₂ отношения, заданные на множестве X. Приведите доказательство:

Доказать, что если отношения R₁ и R₂ симметричны, то симметрично отношение R₁\ R_2.

Теоретическая часть:

Отношением на произвольном множестве называется пара .

- область задания, - график.

- область определения.

- область значений.

Отношение :

-симметричное, если: ,единицы симметричны главной диагонали матрицы смежности;

- несимметричное, если: ;

- антисимметричное, если: ,нет ни одной симметричной пары единиц относительно главной диагонали матрицы смежности и на главной диагонали матрицы смежности единицы;

Пусть имеем и , тогда

Практическая часть:

Пусть R₁AA и

R₂AA

Т.к. R₁ и R₂ симметричны, то

(a,b)AA aR1b→ bR1a, (c,d) AA cR2d→ dR2c

(a,b), (c,d) AA aR1b\ cR2d→ bR1a\ dR2c

пусть R₁\R₂=R (a,b), (c,d) AA aR1b\ cR2d→ bR1a\ dR2c 

(e,f) AA eRf→ fRe  R₁\R₂ –симметрично. Ч.т.д.

Задание 7

Задайте морфизмы между отношениями, являющиеся:

1. Эпиморфизмом;

2. Изоморфизмом;

Теоретическая часть:

Морфизм – перенесение свойств одного объекта на другой.

В дискретной математике под функцией подразумевается отображение некоторого множества на .

Функцией называется функциональное соответствие:

Область определения:

Область значений:

- тотальная, если:

- инъективная, если:

- всюду определенная, если:

- сюръективная, если:

- биективная, если она тотальная, инъективная, всюду определенная и сюръективная.

и - некоторые отношения, тогда:

;

;

Если , то данный морфизм – гомоморфизм между отношениями.

Если гомоморфизм – инъективен, то он – мономорфизм.

Если гомоморфизм – сюръективен, то он – эпиморфизм.

Если гомоморфизм – биективен, то он – изоморфизм.

Практическая часть:

1 )

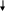
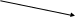
Свойства: функциональность, не всюду определенность, инъективность, сюръективность.

2)

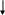
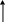
Свойства: функциональность, всюду определенность, инъективность, сюръективность.

Задание 8

Заданы нечеткие множества и , где:

, на четком множестве . Найти нечеткое множество такое что:

8.1) ;

8.2) ;

а также степень нечеткости множеств и .

Теоретическая часть:

- нечеткое множество:

, где - значение функция принадлежности к нечеткому множеству.

Элементы , для которых степень принадлежности к больше нуля – подмножество элементов - носитель .

Логика Заде:

Нечеткое высказывание - предложение или предположение, на основании которого можно судить о степени истинности его в настоящее время.

0 – ложное, 1 – истинное, 0.5 – индифферентно.

Операции нечеткой логики:

- высказывание, степень истинности которого: ;

;

;

;

;

, - нечеткие множества, тогда:

- степень включения в :

- нечетко не включается в .

- нечетко включается в .

- и нечетко равны.

;

;

;

;

Степень нечеткости – отрицание степени равенства и его носителя.

Практическая часть:

8.1)

Для определения значения функции принадлежности использовались определения дополнения и разности нечетких множеств.

8.2)

Для определения значения функции принадлежности использовались определения дополнения и объединения нечетких множеств.

Степень нечеткости:

1)

2)