10. Дифференциальное уравнение движения вязкой жидкости (уравнение Навье-Стокса)

Дифференциальное уравнение движения несжимаемой вязкой жид­кости получается, если к силам, действующим на параллелепипед до­бавить силы трения на гранях(уравнение Навье-Стокса)

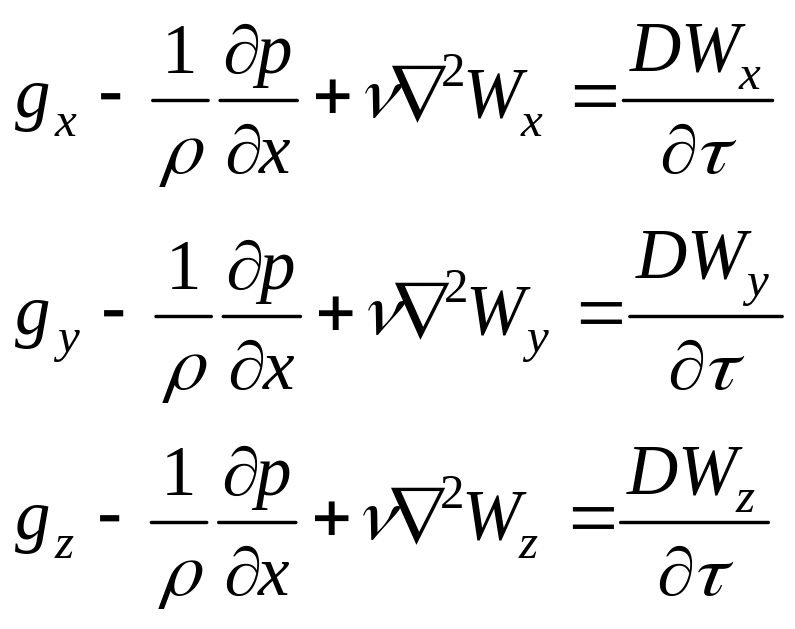(50)

где v - коэффициент динамической вязкости;

, -соответственно суммы вторых производных W по координатным осям;

- субстанциональные производные проекции скорости, учитывающие полное изменение скорости частиц в пото­ке, которое происходит как, вследствие изменения ее в данной точке во времени (локальное изменение ее при неустановившемся течении), так и изменении ее вследствие перемещения частиц в другое место потока (конвективное изменение).

Производные характеризуют изменение скорости во времени в какой то точке, остальные три члена, сто­ящие в правой части уравнения, характеризуют изменение скорости при переходе от точки к точке.

Это уравнение получено без учета зависимости физических параметров жидкости от температуры.

Уравнение неразрывности (сплошности) и уравнение движения газа явля­ется двумя основными уравнениями механики газов. Система, состоящая из двух дифференциальных уравнений, имеет множество решений в соответ­ствии с бесконечным количеством частных случаев течения газа или жидкости. Для однозначности решений этой системы необходимо присоеди­нять дополнительные уравнения, описывающие так называемые краевые условия.

Решение такой системы уравнений - задача математически очень сложная. До сих пор решение удалось получить только для небольшого числа простейших случаев. Однако для понимания задач механики газов и правильного использования в инженерной практике основные дифференциальные уравнения механики газов весьма важны. Одним из наиболее важных случаев является уравнение Бернулли.

11 Уравнение Бернулли и его физический смысл.

Уравнение неразрывности и уравнение Эйлера являются основны­ми в механике газов. Совместное решение этих уравнений дает беско­нечное количество корней. Для однозначности решения необходимо до­бавить уравнение, описывающие краевые условия.

До сих пор удалось получить только для небольшого количества относительно простых случаев. Одним из наиболее важных случаев яв­ляется уравнение Бернулли, и выводу которого мы переходим.

Запишем систему дифференциальных уравнений движения (Эйлера) для элементарной струйки

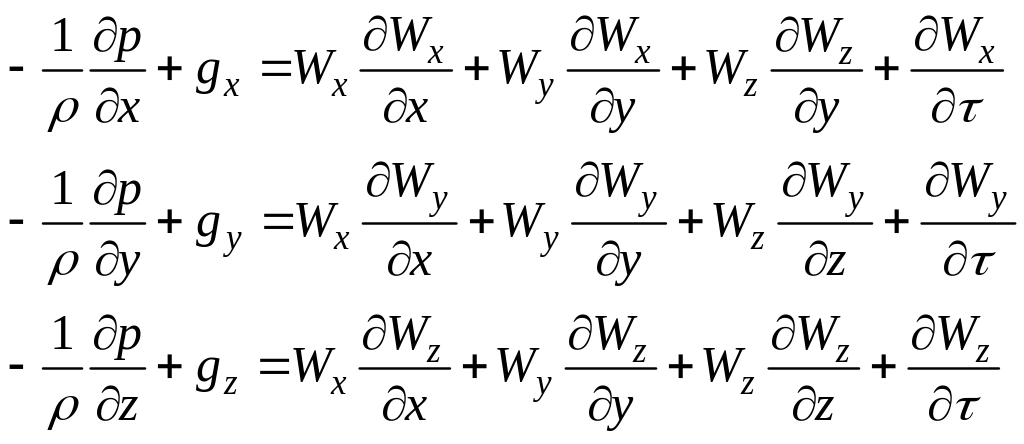(51)

При установившемся движении элементарной струйки , а компоненты скорости изменяются только в направлении соответствующих осей координат. Тогда уравнение Эйлера упростится и примет вид

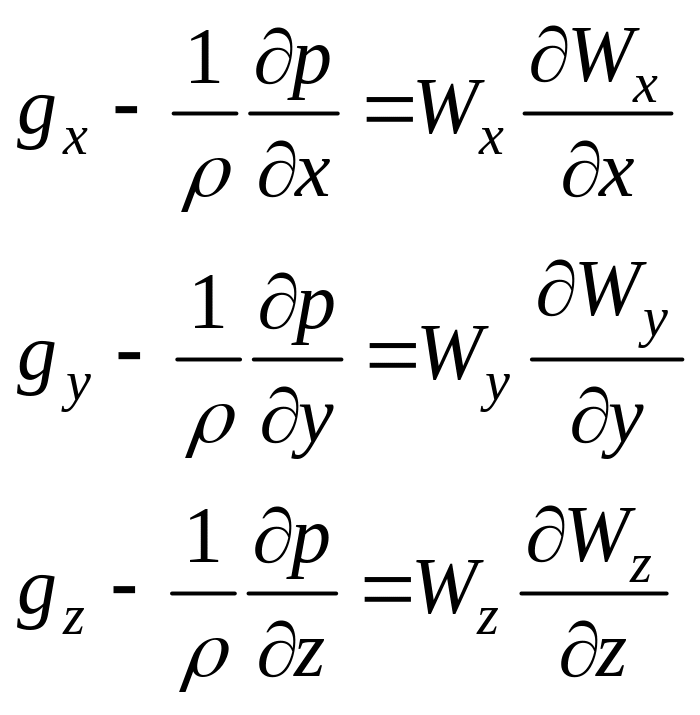(52)

Умножим первое уравнение на dх, второе – на dу, третье – на dz и почленно сложим и составим эквивалентное уравнение

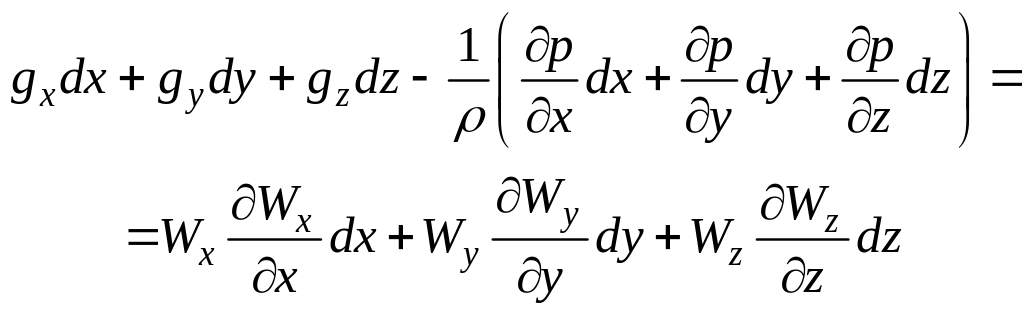(53)

Оси координат разместим так, чтобы g_х = g_у =0, а g_z = -g.

Тогда уравнение примет вид

Выражение, стоящие в скобках представляют полные дифференциалы давления dР и квадрата скорости, т.е.

В следствии этого уравнение можно переписать в виде

(54)

Рассмотрим установившееся течение несжимаемого газа, т.е. такое, при котором скорости в каждой точке не меняется с течением времени ( ).

Интегрируя это уравнение при условии ρ = сопst получим:

,н/м², (55)

где -энергия положения (геометрическое давление) н/м²;

Р- энергия давления (статическое давление), н/м²;

-кинетическая энергия I м³ движущегося газа или жид-

кости ( динамическое давление) н/м² .

Уравнение (55) часто называют уравненем энергии, т.к. размерность н/м² представляет собой энергию 1 м³ потока движущейся жидкости или газа. Разделив все члены на ρ и g получим другой вид уравне­ния Бернулли:

, м (56)

Размерность каждого члена уравнения (56) выражается в м, а это есть энергия единицы веса

Сумма ( )характеризует потенциальную энергию.

Отношение ( ) - кинетическую энергию струйки, отнесенную к 1 кг движущейся среды.

Здесь: z -геометрическая высота (напор), которая выражает энер­гию положения;

-пьезометрическая высота (напор), которая вы-ражает энергию давления, м ;

- скоростная высота (напор), кото­рая выражает кинетическую энергию, м.

Таким образом, полученное уравнение можно прочитать так: при установившемся движении идеальной несжимаемой жидкости вдоль линии тока сумма геометрической, пьезометрической и скоростной высот (на­поров) не изменяется.

С энергетической точки зрения уравнение Бернулли показывает, что сумма потенциальной и кинетической энергии идеальной несжимаемой жидкости есть величи­на постоянная. Полная удельная энергия остается неизменной.

Е_кин + Е_потенц = сопst (57)

Таким образом уравнение Бернулли представляет собой закон сохранения ме­ханической энергии при движении идеальной жидкости. В этом смысле оно имеет фундаментальное значение для гидромеханики.

В практических инженерных задачах пользуются средним значением скорости по сечению реального потока, определяя ее как отношение секундного расхода жидкостей к площади сечения потока:

Действительно, скорость в различных точках сечения отличается от этого значения на некоторую величину ΔW , различную для раз­ных точек по абсолютному значению и по знаку.

Кинетическую энер­гию протекающей через сечение жидкости, отнесенную к I м³ этой жид­кости и определяемую через величину средней скорости, вычисляют сог­ласно выражению:

и уравнение для потока в целом при плавно изменяющемся сечении бу­дет иметь вид:

(58)

Коэффициент α зависит от неравномерности распределения скорос­тей по сечению и называется коэффициентом Кариолиса. Для лами­нарного потока в круглой трубке, где распределение скоростей по сечению соответствует параболе, α=2. Для установившегося тур­булентного течения в трубах.α = 1,1 - 1,13. Уравнение (58) было выведено для жидкости, а для газа - из предположения несжимаемого газа.

Уравнение для идеального газа, учитывающее внутреннюю энер­гию газа, а также подвод или вывод тепла и предназначенное для расчетов, когда меняется температура потока, имеет вид:

, (59)

где U - внутренняя энергия газов при температуре Кдж/кг

Q - величина подводимого или отводимого тепла, Кдж;

А - механический эквивалент тепла

Энергия частиц реальной жидкости или газа, движущаяся в по­токе, не будет оставаться постоянной. Часть энергии будет расходо­ваться на преодоление сопротивлений, возникающих вследствие вяз­кости.

Обозначим потерянную на рассматриваемом участке энергию, от­несенную к 1 м³ движущейся реальной среды, через Δ Р_п . Тогда уравнение Бернулли, написанное для двух сечений реальной жидкости, будет иметь вид

(60)

где - давление положения;

Р -пьезометрическое давление;

- динамическое давление.