9 Дифференциальные уравнения движения идеальной жидкости

Выделим в потоке жидкости элементарный объем в форме паралле­лепипеда со сторонами dx, dy и dz рис.8. Напишем второй за­кон Ньютона для движения массы жидкости этого объема сначала в про­екциях на ось ОХ:

(35)

масса т равна

(36)

Обозначим через W_х, W_у, W_z проекции скорости на оси координат.

Для неустановившегося движения будем иметь:

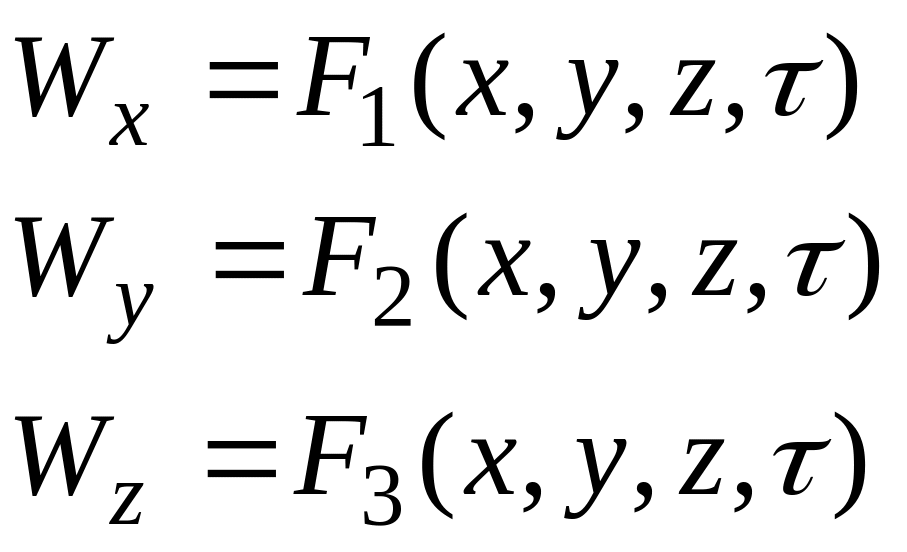
Для установившегося движения

Рис. 8 К выводу уравнения

движения

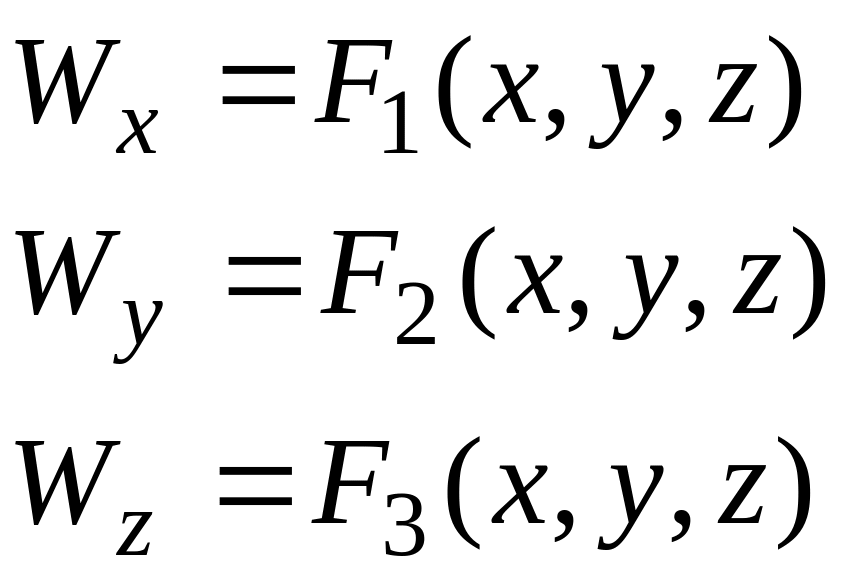
Располагая этими уравнениями, можно определить скорость в точ­ке по величине и направлению, а также ускорение. Проекции ускорения соответственно равны

(37)

В общем случае неустановившегося движения проекции скорости являются функциями координат и времени, поэтому полный дифференци­ал, например, скорости dW_х равен сумме четырех частных дифферен­циалов, а именно:

(38)

а ее производная по времени

(39)

Рассматривая dx, dy и dz как проекции элементарного перемеще­ния dS на оси координат, получим:

(40)

И тогда уравнение (П-45) получит следующую форму записи:

(41)

следовательно:

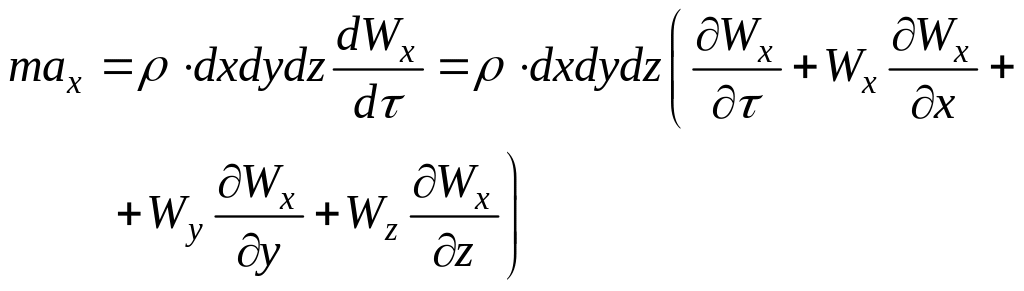(42)

Определим проекцию равнодействующей внешних сил. Проекции силы давления на боковую грань а равна

(43.а)

а на противоположную грань в

(43.б)

Силы давления на другие грани параллелепипеда в проекциях на ось ОХ равны нулю. Сумма проекций сил давления на ось Х будет равна

(44)

Проекцию на ось ох объемных сил можно представить в виде

(45)

где g_х – проекция ускорения.

Запишем проекцию всех сил на ось х

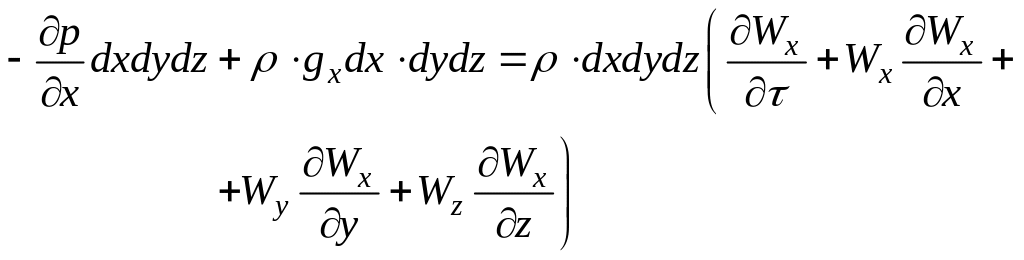(46)

После сокращения на ρ·dx,dy,dz, т.е. отнеся уравнение к единице массы получим

(47)

Аналогичные уравнения можно написать и для других осей. В результате получим следующую систему уравнений

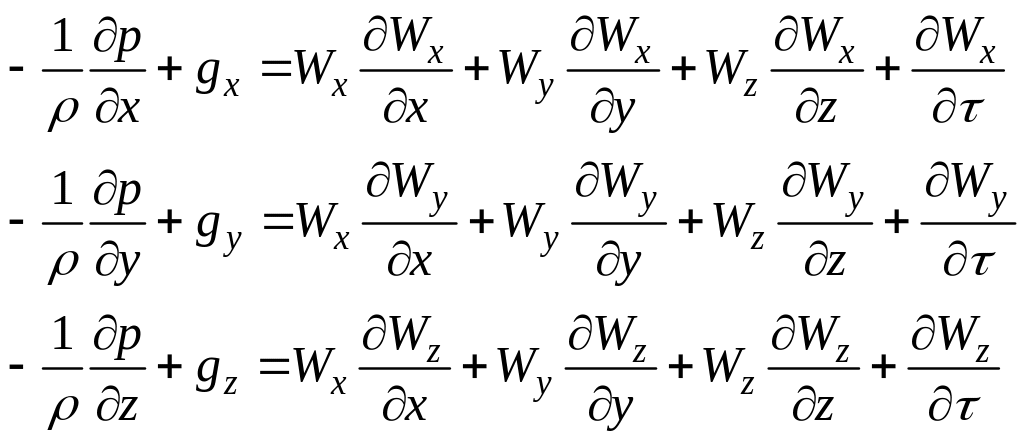(48)

Это и есть система уравнений Эйлера движения сплошной изотропной среды. Эта система описывает движение капельной жидкости (но иде­альной, т.е. невязкой) и газообразной среды, так же лишенной вяз­кости. В эту систему из трех уравнений входят пять неизвестных функций

Поэтому для возможности ее решения необходимо иметь еще два усло­вия, которые связывают между собой названные функции. Такими усло­виями являются уравнения неразрывности (или сплошности) и характе­ристическое уравнение (уравнение состояния). Итак для трехмерного стационарного потока получаем систему уравнений

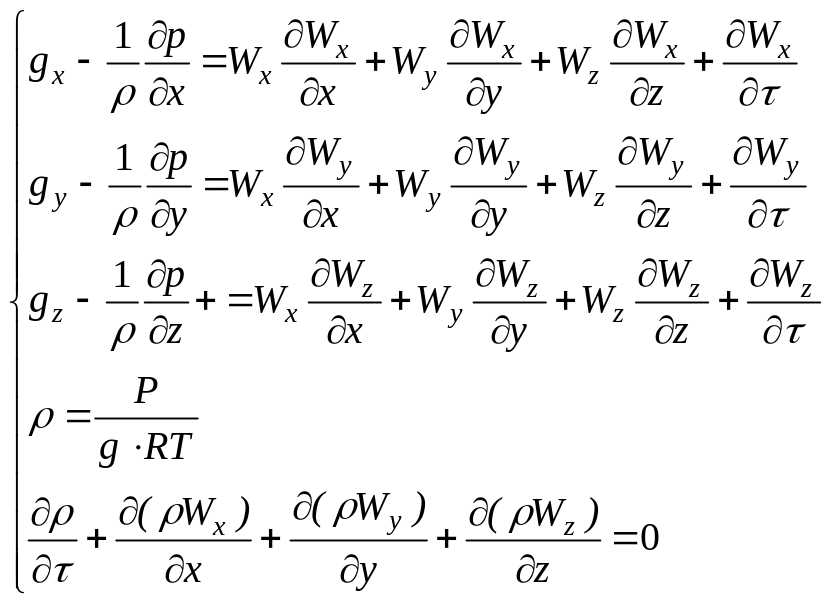(49.а)

Если субстанционную производную записать в общем виде , то систему уравнений Эйлера можно записать в виде

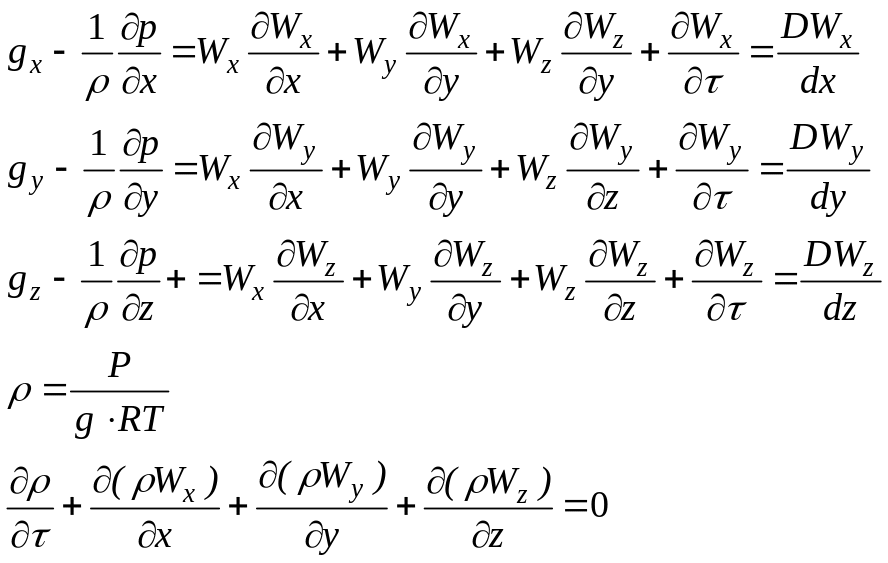(49.б)