8. Уравнение неразрывности движения жидкостей и газов

Теория движения газов строится из предположения неразрывности течения (сплошности). Это основное уравнение газовой динамики мы выведем .для элементарной струйки газа, поперечные размеры которой настолько малы, что в каждом ее сечении можно считать постоянным все основные параметры потока: скорость, давление, температуру и плотность газа.

Чтобы получить уравнение неразрывности, рассмотрим стационар­ное (установившееся) движение элементарной струйки газа (рис.7).

При стационарном движении в любой точке пространства сохраня­ются неизменными во времени скорость движения и состояние жидкости или газа (плотность, давление и температура). Траектория частиц при таком движении называется линиями тока. Боковая поверхность струйки, носящей название поверхности тока, является для жидкости (газа) не­проницаемой.

Рассмотрим некоторый участок элементарной струйки между двумя нормальными поверхностями тока сечениями I и 2, заметим, что в ука­занном на рис.7 направлении 1-2 приток газа осуществляется только через поперечное сечение I, а расход газа только через сечение 2.

Рис.7 К выводу уравнения неразрывности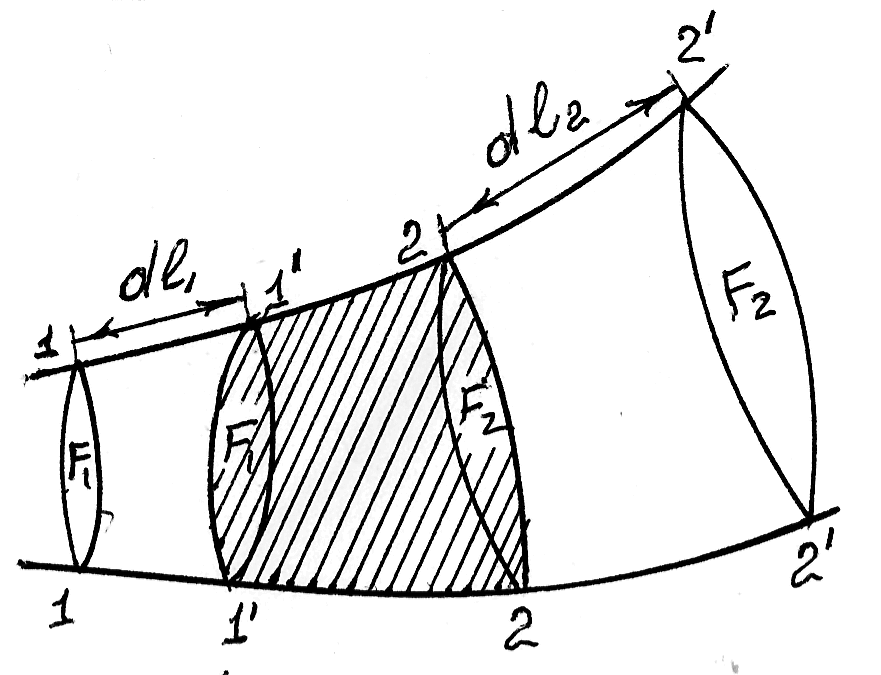

За бесконечно малый промежуток времени dτ выделенная часть струйки переместится в новое положение 1´-2´ . Перемещение состоит в том, что за время dτ заштрихованный объем I´-2 вместит газ, вытесненный из области I-I´, а известное количество газа за то же время вытечет из этого объема и заполнит область 2-2´. Приток газа в объеме 1´-2 составит:

(28)

где ρ₁ - плотность газа в поперечном сечении I

F₁ - площадь поперечного сечения I .

Расстояние между сечениями I и I´ равно произведению скорости движения на элементарный промежуток времени.

(29)

где W₁ - скорость в сечении I, откуда

(30.а)

Расход газа из объема 1´-2 равен, очевидно

(30.б)

При установившемся режиме и отсутствии разрывов сплошности в движущейся среде приток газа должен равняться расходу:

(31.а)

Отсюда, после соответствующей подстановки, получаем уравнение нераз­рывности- закон сохранения массы для единичной струйки жидкости или газа при установившемся течении

(31.б)

В случае несжимаемой жидкости, т.е. при ρ = const уравнение (31.б) принимает более простую форму

(32)

Уравнение постоянства расхода газа G =gρWF = const можно пред­ставить так же в дифференциальной форме

поделив почленно это соотношение на , получим

(33)

В общем случае неразрывного движения сжимаемой жидкости уравнение неразрывности имеет вид

(34)

- это закон сохранения энергии.