7. Дифференциальное уравнение статики идеальной жидкости (уравнение Эйлера).

Перед тем, как начать изучать движение газов, следует рассмот­реть условие их равновесия. Это необходимо для выяснения условий поведения газа при малых скоростях движения, где его состояние близ­ко к равновесному, и для получения исходных предпосылок для последующих выводов. При этом изучают зависимость давления в данной точке от объемного веса газа и геометрического положения точки.

При выводе основных соотношений статики газов исходят из сле­дующих положений:

1. Газ или жидкость находится в равновесии, если для каждой произвольно выбранной части объема результирующая всех при­ложенных сил будет равна нулю.

2. Для любой выделенной части поверхности газа (жидкости), нахо­дящегося в равновесии, поверхностные силы перпендикулярны к поверхности и направлены внутрь ее.

Для вывода уравнения равновесия жидкости выделим в ней элемен­тарный прямоугольный параллелепипед с ребрами

dх, dу, dz и объемом dV=dx,dy,dz на этот параллелепипед действуют силы тяжести и силы давления, действующие на. каждую грань (рис.5 ).

Обозначим проекции ускорения силы тяжести на оси координат через g_x, g_y ,g_z. Тогда проекции самой силы тяжести на оси координат будут соответственно равняться

(17)

Эти силы должны быть уравновешены разностью давлений, приходя­щейся на соответствующие грани параллелепипеда.

При переходе от одной грани к противоположной давление, в общем случае, Р должно изменяться.

Рис. 5 К выводу уравнения

движения Эйлера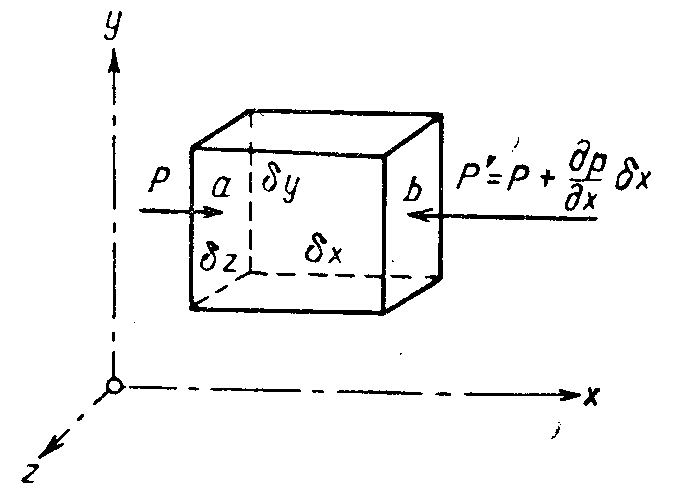

И поэтому силу давления на грань «а» и на противоположную грань «в» можно запи­сать

Сила на грань «в» войдет в уравнение проекций со знаком минус.

И для грани, перпендикулярной к оси X, равнодействующая сил давле­ния равна:

(18)

Проек­ция объемной силы равна произведению массы ρ·dx·dy ·dz на проекцию ускорения g_x , если рассматривать направление по оси Х.

ρ·dx·dy ·dz · g_x = g_x ·ρ·dV (19)

а сумма сил, действующих в направлении оси X равна:

(20)

Если уравнение разделим на ρ·dV, получим

=0

Условие равновесия для всех трех координат будет иметь следующий вид:

(21)

или

(21.б)

Эта система носит название системы уравнений Эйлера- уравнений статики жидкости и газа. Умножил уравнение (2.17) первое на dх и последующее на dу, dz

и, склады­вая их, получим:

Трехчлен в левой части уравнения (2.18) представляет полный дифференциал давления, поэтому

(23)

Это уравнение называют основным уравнением статики жидкостей и газов. Уравнение (2.19) содержит две неизвестных функции Р и ρ поэтому для решения необходимо еще одно урав-нение. Таким является так называемое характеристическое уравнение или уравнение состояния, которое, в общем случае, определяет зависимость плотности от давления и температуры. Таким образом для газов уравнением состоя­ния является уравнение Клапейрона –Менделеева

,

где Р - абсолютное давление;

R - газовая постоянная, разная для различных газов, но не

зависящая от температу­ры и давления;

Т - абсолютная температура.

Если направить силу тяжести по координате у, то

(24)

Интегрируя последнее уравнение, получим:

Постоянную интегрирования С определяем из уравнения (2.21) в условиях сечения у_о, где газ соприкасается с атмосферой и имеет давление Р_о. Подставим вместо у = у_о и Р= Ро получим

(25)

Далее можно рассмотреть два случая.

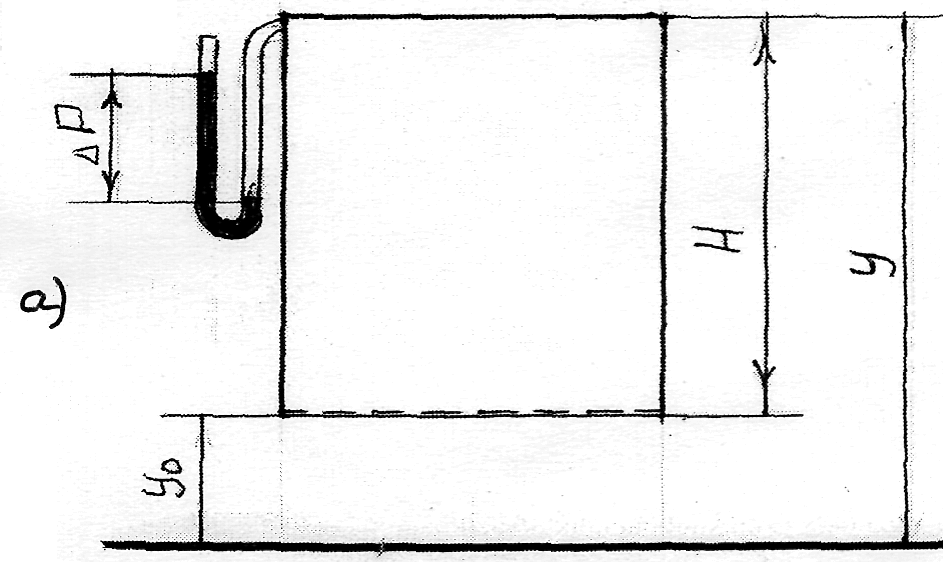
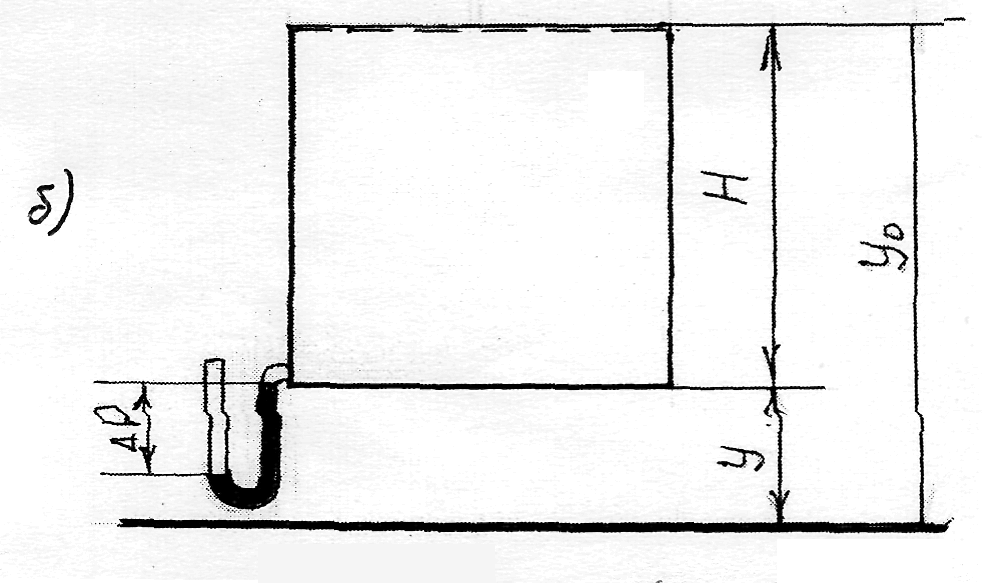
Рис.6 К определению следствий из уравнения Эйлера

В первом случае (рис.6 а) газ соприкасается с воздухом снизу своего объема Обозначим разность геометрических отметок через Н = у - у_о (у > у_о) , получим:

Р = Р_о - ρ·gН

Если в сосуде на высоте Н поставить Vобразный манометр, то он покажет разность давлений ΔР между сосудом и окружающим воздухом, равную ΔР= Р_г –Р_в

(26)

где - соответственно плотности холодного воздуха и

горячего газа.

Т.к. ρ_в >ρ_г, то ΔР > 0, т.е. должно быть положительное давление. Этот вывод подтверждается практикой работы печей, в кото­рых наблюдается увеличение давления газов от пода печи к своду.

Во втором случае газ соприкасается с воздухом в верхней части занимаемого объема, как видно из рисунка 6.б. При этом

у > у_о и Н = у_о - у отсюда

Р = Р_о + ρ·gН

Рассуждая аналогично предыдущему, будем иметь

(27)

Эта зависимость лежит в основе расчета статики дымовых труб, т.е. можно рассчитать статическое разряжение у основания дымовой трубы.