3. Вязкость жидкостей и газов.

Вязкостью называется свойство жидкости оказывать сопротив­ление сдвигу. Все реальные жидкости обладают определенной вяз­костью, которая проявляется в виде внутреннего трения при отно­сительном перемещении смежных частиц жидкости.

Вязкость харак­теризуется степень текучести жидкости или подвижности ее час­тиц.

При ламинарном течении жидкости можно представить в виде слоев, которые скользят один относительно другого.

Рассмотрим два слоя жидкости, движущиеся на расстоянии Δy друг от друга (рис.1). Один слой движется со скоростью W, а дру­гой - со скоростью W + ΔW. Между ними возникает разность скоростей ΔW. Величина ΔW является абсолютным

Рис.1 К понятию «внутреннее трение»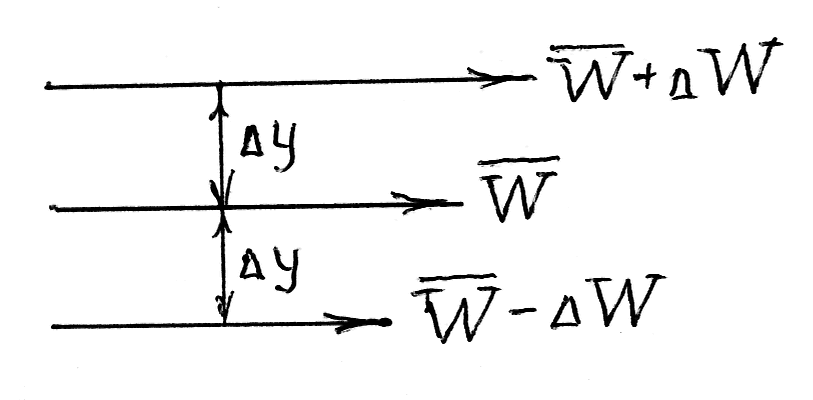

сдвигом слоя 1 по слою 2, а есть градиент скорости (относительный сдвиг). Появляющиеся при этом движении касательные напряжения (сила трения на единицу площади) обозначим через τ. Тогда аналогично явлению сдвига в твёрдых телах мы получим следующую зависимость между напряжением и деформацией.

(9.а)

Если возьмем предел этого отношения, то получим выражение

, (9.б)

Величина μ, аналогичная коэффициенту сдвига в твёрдых телах и характеризующая сопротивляемость жидкости сдвигу, назы­вается коэффициентом внутреннего трения или коэффициентом динамической вязкости.

- градиент скорости в направлении, нормальном к слоям жидкости; τ - касательные напряжения, т.е. сила трения, отнесен­ная единице поверхности, которая расположится вдоль по потоку между слоями.

На существование уравнения (9.б) обратил своё внимание Ньютон, который и сформулировал общеизвестный закон. Касательное напряжение трения между двумя слоями пря­молинейно движущейся вязкой жидкости (газа) пропорционально от­несенному к единице длины изменению скорости по нормали к нап­равлению движения. Жидкости подчиняющиеся этому закону называются Ньютоновкими и составляют большенство всех жидкостей. Следовательно, вязкость принадлежит к числу явлений переноса импульса движения. Сила внутреннего трения в жидкости равна.

, (10)

т.е. она прямопропорциональна градиенту скорости, площади тру­щихся слоев и коэффициенту вязкости (трение в жидкости отлича­ется от трения в твёрдых телах, где силы трения зависят от нормального давления и не зависят от площади трущихся частей).

Для определения размерности динамического коэффициента вязкости по уравнению (9.б) получим

= нс/м² или Па·с

В международной системе единиц СИ коэффициент динамичес­кой вязкости выражается в ньютон-секундах на квадратный метр ( н^.с/м²).

В старой технической системе единиц измерения коэффициент динамической вязкости имеет размерность кг · с/см² .

Вязкость жидкостей в сильной степени зависит от температуры: вязкость капельных жидкостей при увеличении температуры умень­шается, а вязкость газов возрастает. Это объясняется тем, что в газах интенсивность теплового движения (средняя скорость) мо­лекул с повышением температуры возрастает и, следовательно, воз­растает коэффициент вязкости. В капельных жидкостях молекулы не могут, как в газе, двигаться по всем направлениям, они могут лишь колебаться около своего среднего положения. С повышением температуры средние скорости колебательных движений молекул уве­личиваются, благодаря чему легче преодолеваются удерживающие их связи.

Зависимость коэффициента внутреннего трения газов от тем­пературы определяется по формуле, найденной опытным путём

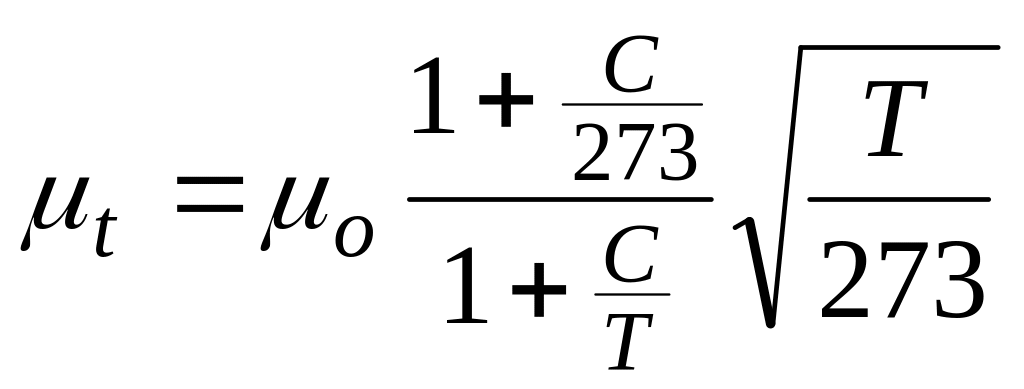, (11)

где μ_о - вязкость газов при 0°С.

Т - абсолютная температура газа.

С - постоянная величина, зависящая от вида газа.

Наряду с понятием абсолютной или динамической вязкости в механике газов нашло применение кинематическая вяз-кость (кинематический коэффициент вязкости) представляющий собой отношение абсолютной вязкости жидкости или газов к плотности

Название кинематической вязкости вытекает из того, что в размерности этой величины отсутствуют единицы силы. В самом деле, представим размерность μ и ρ , получим:

Кинематический коэффициент вязкости капельных жидкостей при давлениях до 200 бар весьма мало зависит от давления при обычных гидравлических расчётах не учитывается.

Кинематический коэффициент вязкости газов зависит от температуры и давления, возрастая с увеличением температуры и уменьшаясь с увеличением давления (табл.1)

Таблица.1 Кинематический коэффициент вязкости некоторых

газов (при давлении 1,01 бар)

Наименование газа	v.105, м2/сек	Температура, оС
Воздух Водород Гелий Кислород Углекислый газ Метан Природный газ Саратовского месторождения	1,45 9,45 10,6 1,40 0,72 1,48 1,40	15 15 15 15 15 20 0

Важнейшими свойствами газов являются плотность и удельный объем.

Плотностью называется масса единицы объема, т.е. отношение массы к ее объему

, кг/м³

Наряду с плотностью часто используют понятие «удельный вес». Удельным весом называется вес единицы объема

, н/м³

В технической термодинамике и в некоторых разделах газодинамики в качестве величин, характеризующие плотностные качества газа, пользуются понятием «удельный объем», который представляет объем, занимаемый единицей массы газа

, м³/кг