21 Движение газов с высокими скоростями

Основные формулы адиабатного течения идеального газа.

При движении газа с большими скоростями (обычно выше 150 м/с) в потоке возникают значительные перепады давлений, в результате чего плотность газа может сильно изменяться. Изме­нение плотности в свою очередь влияет на скорость, что делает невозможным применение к газам методов расчета несжимаемых жидкостей.

Рассмотрим установившееся движение газа в элементарной струйке. На основании закона сохранения массы можно записать

dМ₁ = dМ₂

где М₁ и М₂ – масса газа до и после истечения.

Для реального газа в процессе перехода элемент dV получает тепло и совершает работу. Опуская вывод можно записать уравнение энергии движущегося газа

, Дж/кг (115)

где q_м – удельное тепло, поступающее извне;

q_т – удельное тепло, выделяемое в результате трения;

W₁,W₂ – скорость в начале и конце рассматриваемого

участка;

z_1, z₂ – координаты (по вертикали) начального и конечного

участка;

h₁ ,h₂ – энтальпия среды в начале и конце участка;

l_т – работа трения.

Основным для расчета одномерного движения газа является представленное уравнение (115). В большинстве задач газовой динамики изменение удельной потенциальной энергии мало по сравнению с изменением кинетической энергии . Поэтому второй член правой части уравнения (115) принимают равным нулю.

Встречающиеся на практике случаи течения с высокими скоростями обычно не сопровождаются существенным теплообменом газа с окружающей средой, поэтому теплообменом на единицу массы газа можно пренебречь и считать течение адиабатным ( q_м = 0). Теплота, выделяющееся при трении, равна работе трения q_т = l_т). В результате из уравнения (115) получаем уравнение энергии для адиабатного течения.

(116)

Так как h = с_рТ, то в соответствии с уравнением (116) при адиа­батном течении с возрастанием скорости газ охлаждается, а с умень­шением разогревается.

Используя уравне­ние Клапейрона-Менделеева

, (117а)

а так же уравнение энтальпии

, (117б)

а так же значения с_v и с_р

, (117.в)

где , представим уравне­ние (1-94) в механической форме:

(118)

Уравнение энергии в форме (118) связывает скорость с плот­ностью и давлением газа, аналогично уравнению Бернулли для несжимаемой жидкости.

Если применить уравнение (118) к двум сечениям струйки, в одном из которых поток заторможен до W = 0 (или не начал движение), то с помощью формул (117.б) и (116) получим

, (119)

т. е. вся кинетическая энергия переходит в энтальпию. Если торможение изоэнтропическое, то энтальпия может снова пере­ходить в кинетическую энергию. Из уравнений (119) следует, что величины р_о ρ_о, h_о, Т_о являются характеристиками данного потока. Их называют параметрами торможения.

Скорость звука в газе за­висит от скорости его движе­ния. Обозначив скорость звука в неподвижном газе через а_о, с помощью уравнений и (119) получим

(120)

т. е. что при ускорении газа скорость звука в нем уменьшается . Следовательно, поток можно разогнать настолько, что его скорость станет равной скорости звука. Такая скорость w_* называется критической, а все параметры газа с критической скоростью - критическими параметрами.

В газовой динамике часто используют число Маха, предста­вляющее собой отношение скорости потока к местной скорости звука:

М =W/a

и коэффициент скорости, представляющий собой отношение скорости потока к критической скорости

λ' = W/W_*

Поток, скорость которого меньше местной скорости звука (W < а, М < 1), называют дозвуковым. При W = а, М = 1 течение называется звуковым или критическим. При W > а, М > 1 течение называется сверхзвуковым, а М > 5 – гиперзвуковым.

Связь между критическими параметрами и параметрами тормо­жения описываются уравнениями

(121.а)

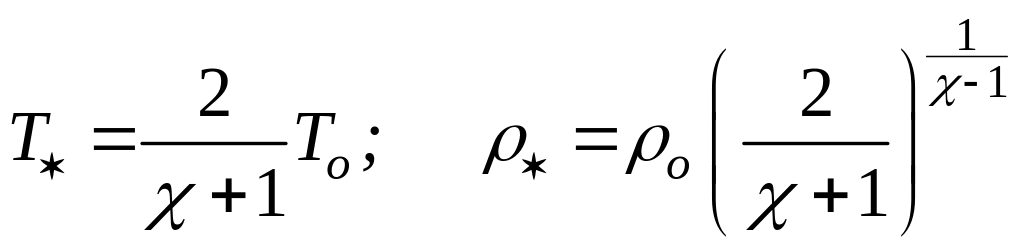(121.б)

Две последние формулы справедливы только для изоэнтропного течения. При заданных параметрах торможения поток приобре­тет максимальную скорость, если вся энтальпия перейдет в кине­тическую энергию. Согласно уравнению (119), максимальная скорость достигается при истечении в вакуум (р = 0):

(122)

Суживающееся сопло. Суживающиеся сопла служат для ускорения дозвуко­вых потоков газа (рис.25).

Рис. 25 Скорость и давление газа при истечении через простое сопло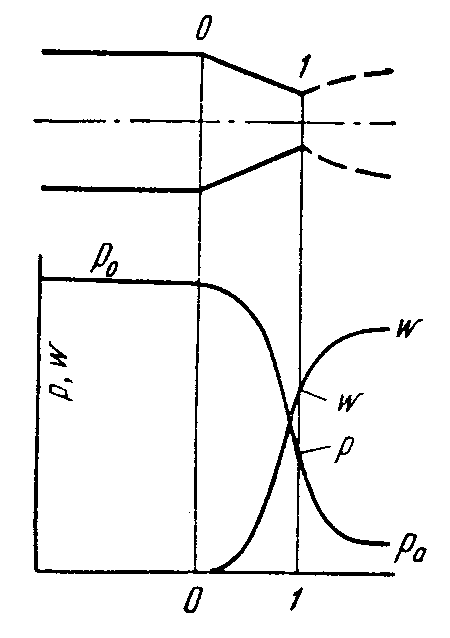

К соплу поток газа обычно подводится по трубе. Чтобы обеспечить в трубе минимальные потери энергии на трение, ее сечение выбирают достаточно большим, благодаря чему скорость получается низкой. Так как в уравнение энергии (116), которым пользуются для расчета сопла, скорости взяты в квадрате, то . Таким образом, скорость в трубе перед соплом W₀ можно считать равной нулю, а давление и плотность газа равными соот­ветствующим параметрам торможения. На коротком участке сопла можно пренебречь теплообменом и потерями энергии на трение и считать течение изоэнтропическим.

Скорость истечения из соп­ла можно найти из уравнения (119), заменив в нем величину ρ₁ с помощью уравнения адиабаты

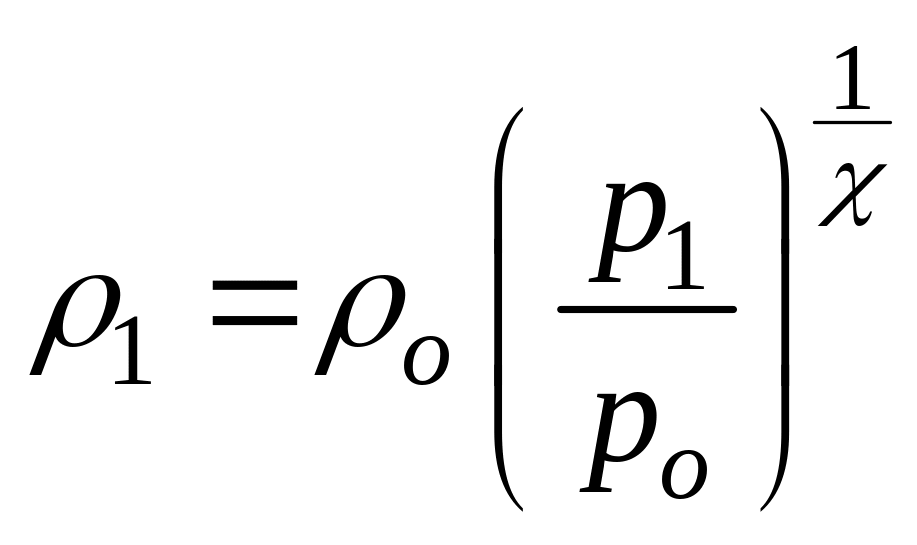(123)

Проведя алгебраические преобра­зования, получим

(124)

Формула (124) называется урав­нением Сен-Венана и Ванцеля. Расход газа через сопло опре­деляется с помощью формулы, в которую подставляют зна­чения ρ и w по формулам (123) и (124):

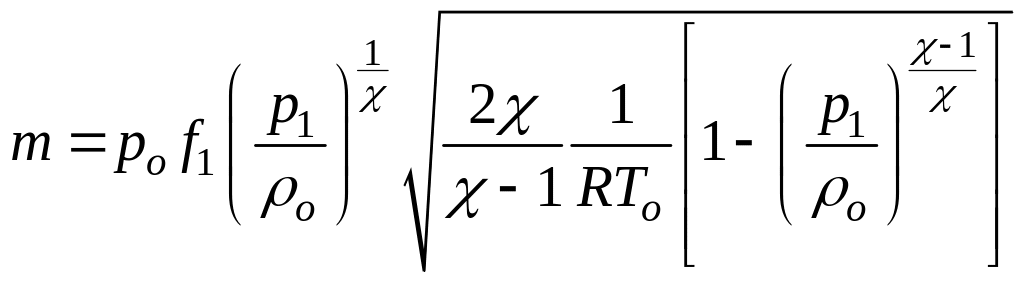(125)

Формулы (124) и (125) применяют, когда известно давление на срезе сопла. В частности, при дозвуковом истечении оно равно давлению окружающей среды (р₁ = р_а).

При достижении критической скорости ( w = w_* ) в сопле устанавливается критическое давление (р₁ = р_*), которое, как указывалось, зависит только от давления торможения. Подставив в формулы (124) и (125) отношение р_*/р_о из формулы

(121.б), получим для критической скорости выражение (121.а), а для крити­ческого расхода следующую формулу:

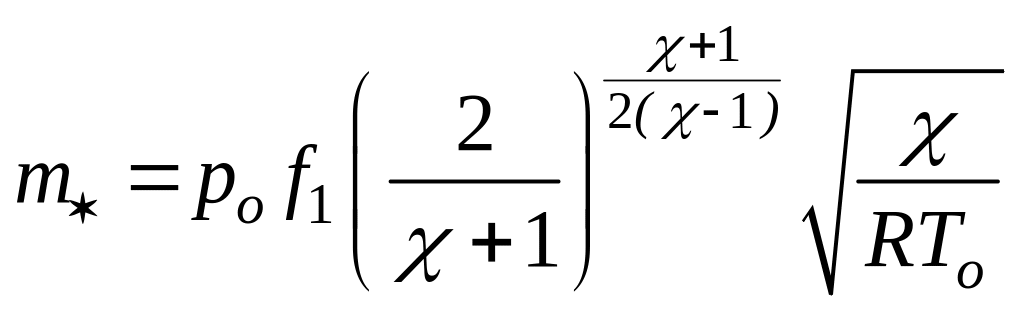(126)

Если повышать давление перед соплом (р₀) при постоянной температуре Т₀ (это часто встречается на практике), то согласно формуле (126) для данного газа

т. е. при истечении с критической скоростью массовый расход прямо пропорционален давлению перед соплом.

Практически сопла не обеспечивают расчетные характеристики потока. Поэтому истинный расход получают, умножая теоретиче­ский расход на коэффициент расхода μ_с ≈ 0,92.

Обычно центральный угол сужения сопла принимают в пре­делах 30-60°. Во избежание излишних потерь энергии поверх­ность сопла необходимо делать гладкой без заусенцев и шероховатости.

Сверхзвуковое сопло (сопло Лаваля).В ряде устройств (форсунках, фурмах, эжекторах, реактивных двигателях и др.) желательно иметь сверхзвуковые скорости истечения. Для создания таких скоростей применяют сопла Лаваля.

Рис. 26 Схема сопла Лаваля

Сверхзвуковое сопло состоит из сужающейся и расширяющейся частей (рис.26). В соответствии с уравнением Гюгонио в су­жаю-щейся части скорость газа может воз­расти до критического значения, которое до­стигается в самом узком сечении, называе­мом критическим. В расширяющейся части должно происходить дальнейшее ускорение газа до сверхзвуковых скоростей. Течение газа в сужающейся части подчиняется тем же законам, что и в простом сопле.

Близкие к расчетным характеристики можно получить с по­мощью сопел, имеющих сложный профиль. Однако ради простоты изготовления сужающуюся и расширяющуюся части выполняют коническими. Центральный угол сужения равен 30-60°, цен­тральный угол расширения 8-14°. Сопряжение конусов закруг­ляют, но так, чтобы фактическое проходное сечение горловины равнялось критическому.

Фактические скорость и расход через сопла меньше расчетных. Поэтому расход по формуле (126) следует умножить на коэффи­циент расхода μ_с ≈ 0,92., а скорость по формуле (124) - на коэффициент скорости φ = 0,95.