16.4 Измерение скорости и расхода потока

Простейшим прибором для измерения скорости в открытом пото­ке служит трубка Пито (рис.18). Она представляет собой изогнутую трубку небольшого диаметра, установлен­ную в потоке движущейся жидкости открытым концом навстречу течению, и так, что ось трубки совпадает с направлением потока.

Рис. 18 Трубка Пито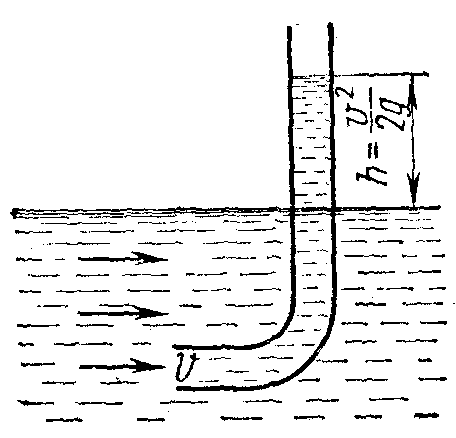

При этом в вертикальной части трубки

жидкость поднимется на высоту h, равную скоростному напору:

Откуда

Фактически наличие трубки в потоке несколько искажает общее распределение скорости, и поэтому при ее определении в формулу вводят поправочный коэффициент

(98)

Коэффициент ξ₁ находят экспериментально для каждой трубки.

Трубку Пито можно использовать .и для измерения скорости в за­крытых трубопроводах (рис.19, а), применяя ее совместно с обычной пьезометрической трубкой. Трубка Пито показывает полный напор жидкости в трубе , а пьезометрическая трубка – статический напор — в том же сечении трубы. Разность этих напоров равна разности ∆h уровней в обеих трубках. Таким образом

Для того чтобы учесть влияние вязкости и внесенное трубкой из­менение в распределение скоростей и давлений в потоке, так же как и для трубки Пито, вводят поправочный коэффициент ξ

Расход жидкости измеряют трубкой Вентури (рис.20). Составим уравнение Бернулли для сечений 1-1 и 2-2 и, преобразуя, получим

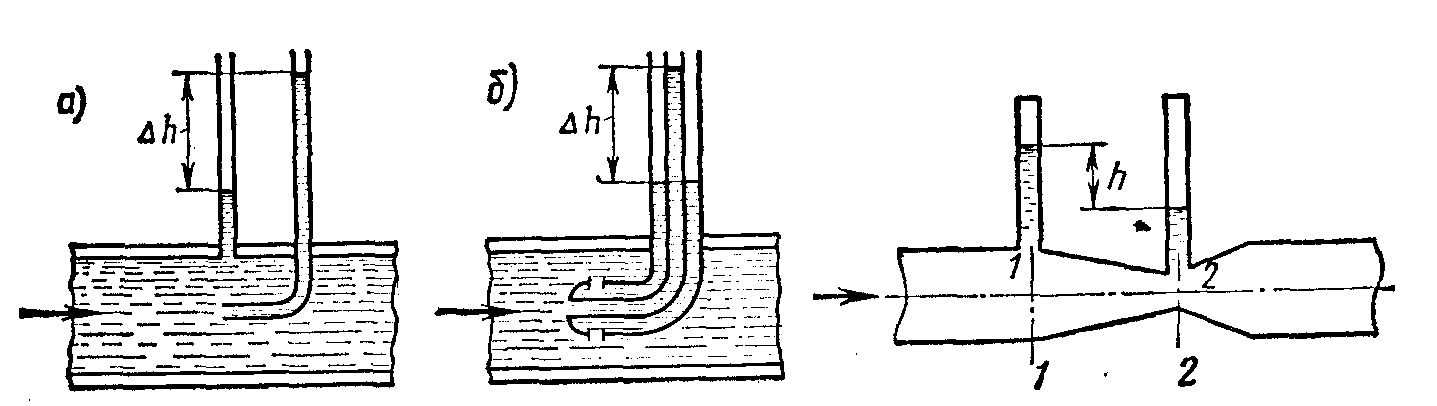
Рис. 19. Трубка Прандтля Рис. 20. Трубка Вентури

,

но = h

поэтому (99)

Из уравнения неразрывности имеем

Подставив значения W₁ и W₂ в формулу (3.48) и решив полученное уравнение относительно Q, найдем

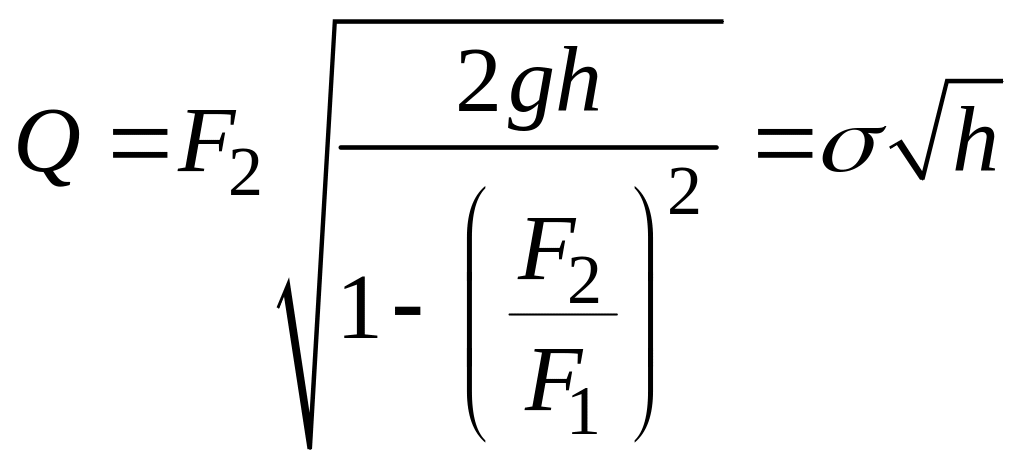, (100)

где 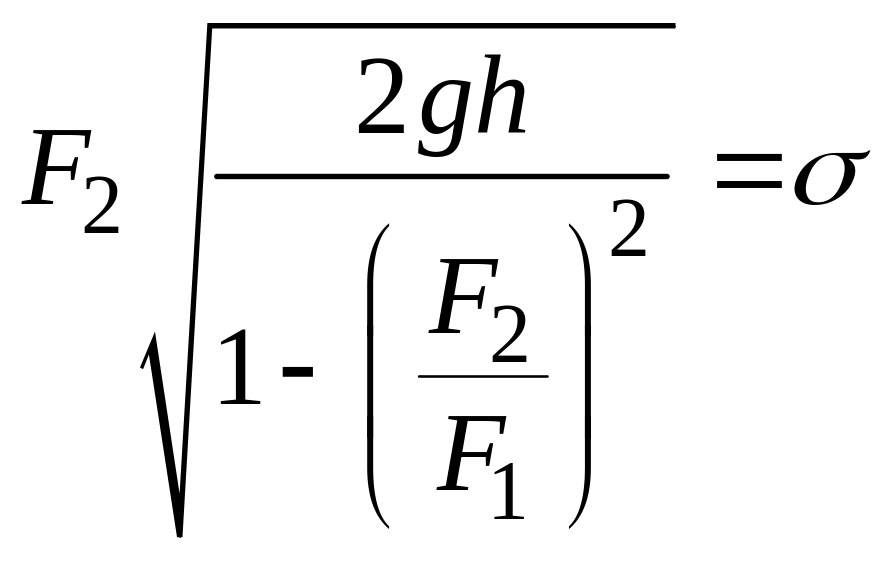- постоянная величина, которую обычно

определяют при градуировке прибора.

16. 5 Понятие об эквивалентном отверстии.

Анализируя формулу (43) можно установить, что при V=сопst чем меньше F, тем больше значение W , а, следовательно, и ΔР. Сделав отверстие очень малым, можно использовать эту формулу для создания весьма больших перепадов давления.

Пользуясь этим обстоятельством при изотермическом течении га­за, можно сопротивление при движении любого газа, в общей сумме характеризующееся потерями напора ΔР, заменить сопротивлением с острыми краями. Такое отверстие называется эквивалентным.

Удобство использования понятия "эквивалентного отверстия" за­ключается в том, что зная величину сопротивления ΔР (перепад дав­лений) для данного значения V, легко найти ΔР' для любого значения V'.

В самом деле:

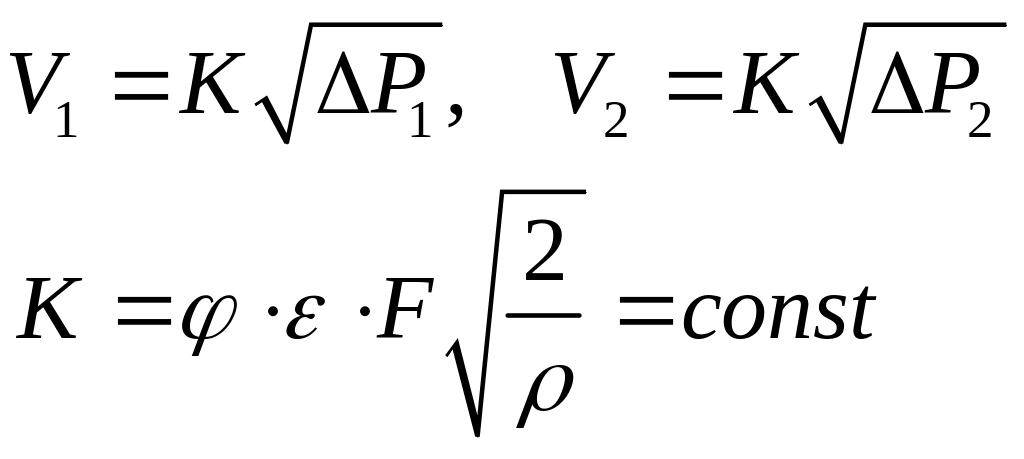
Если разделить одно уравнение на другое, получим:

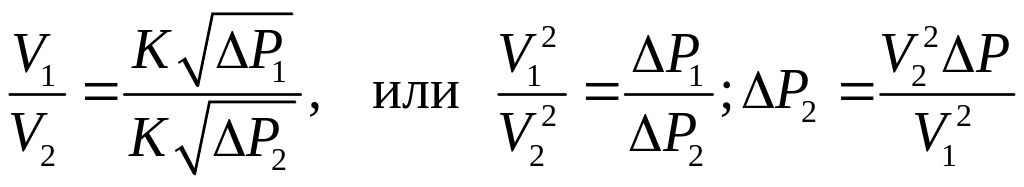(101)

Такой способ применим к движению продуктов горения и газов при условии ρ_г=сопst. В остальных случаях им можно пользоваться как приближенным методом.