15 Потери энергии при движении жидкостей и газов

При движении жидкости и газа по тубопроводам, каналам происходит частичная потеря энергии. Все источники потерь энергии подразделяются на два вида – потери напора (энергии) на трение (потери по длине) Р_тр и местные потери напора (энергии) Р_м.с

Линейные потери напора. Линейные потери напора пред­ставляют собой потери на преодоление внутреннего трения между раз­личными слоями жидкости, движущимися относительно друг друга. Поэтому величина внутреннего трения существенно зависит от рас­пределения скоростей в потоке, а следовательно, и от режима течения жидкости.

Найдем сначала потерю напора Р_тр при стационарном ламинарном течении в круглой трубе. Выделим мысленно в жидкости соосный с трубой цилиндр длиной l и радиусом у. С внешней стороны на по­верхность цилиндра действует касательное напряжение вязкого трения, которое равно

Следовательно, на всю поверхность цилиндра F = 2уl действует сила

(79)

Поскольку течение стационарно, то эта сила уравновешивается раз­ностью сил давления р₁ у² и р₂ у² на торцах цилиндра. Таким об­разом

,

откуда

(80)

Учитывая граничное условие W = 0 при у = r, где r - радиус тру­бы, проинтегрируем правую часть последнего уравнения от у до r, а левую соответственно от 0 до W

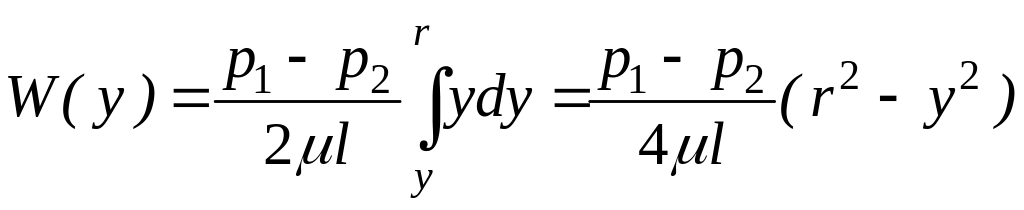(81)

Таким образом, при ламинарном течении вязкой жидкости по круг­лому трубопроводу распределение скоростей в потоке имеет параболи­ческий характер рис.12.а.

Интегрируя формулу (81) по поперечному сечению потока, по­лучим формулу Пуазейля для определения секундного расхода Q жидкости:

(82)

Используя равенства (82) и (Q = WF), можно определить среднюю ско­рость W_ср потока, с которой обычно приходится иметь дело во всех гидравлических расчетах. Обычно индекс «ср» отбрасывают и среднюю скорость обозначают через 

(83)

С помощью последней фор­мулы найдем перепад давле­ний р₁ -р₂ и определим ве­личину линейной потери h_

(84)

Из полученной, формулы видно, что при ламинарном установившем­ся течении величина Р_тр пропорциональна скорости потока. Если вместо радиуса трубы r использовать ее диаметр d= 2r и число Рейнольдса , то формулу (84) можно привести к виду

(85)

Уравнение (85) может быть использовано при любых режимах течения жидкости и записывают его в виде формулы Дарси- Вейсбаха:

(86)

где  - коэффициент трения, являющийся функцией числа

Рейнольдса.

При стабилизированном ламинарном течении в круглой трубе ве­личина  определяется формулой Пуазейля:

Распределение скоростей в турбулентном потоке не имеет параболического характера (рис.12.б), а коэффициент трения

и его зависимость от числа Рейнольдса определяется степенью шероховато­сти стенок труб,

Эту зависимость в 1932 г. экспериментально исследовал Никурадзе на трубах с искусственной равномерной шероховатостью. Результаты его исследований представлены на рис.13, где по оси ординат от­ложен , а по оси абсцисс -

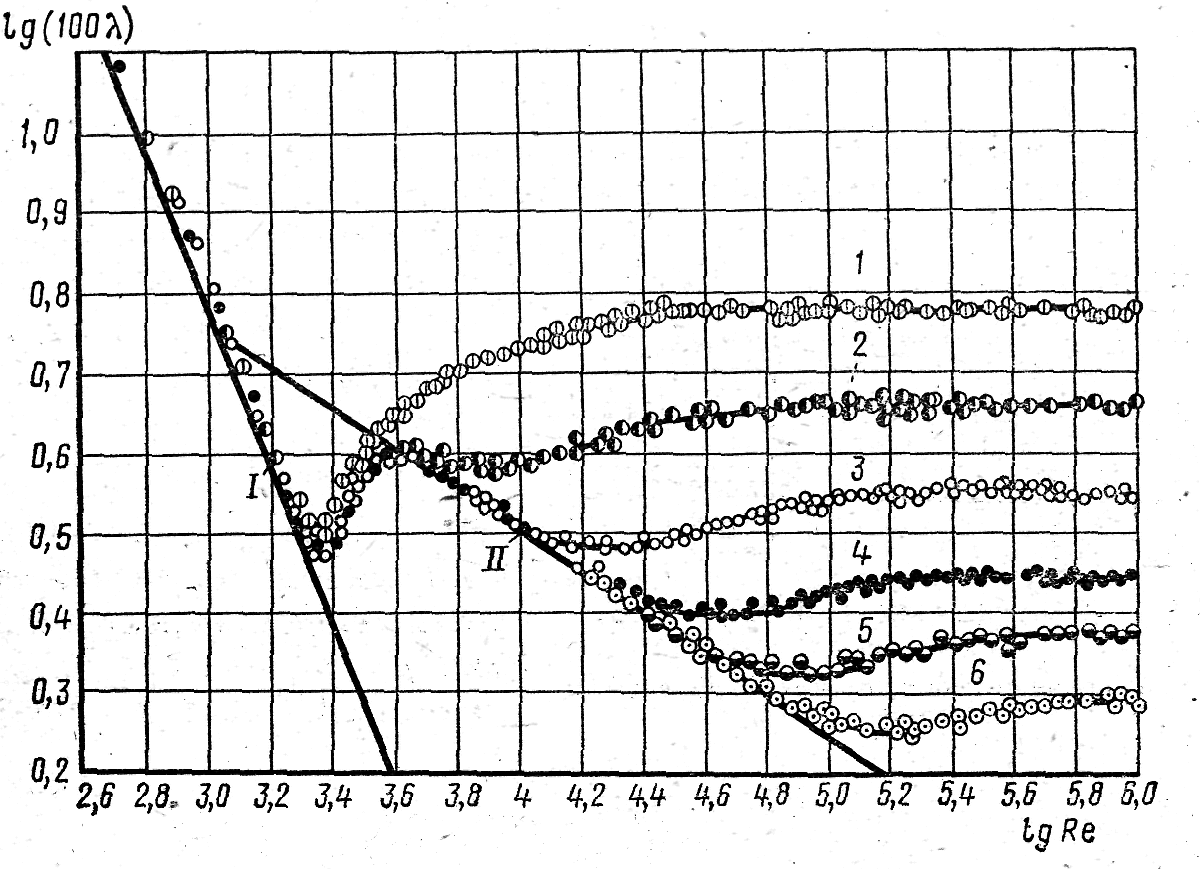
Рис.13 Результаты опытов Никурадзе

На рисунке представлены шесть кривых, полученных для труб с различной относительной ше­роховатостью, которая характеризуется безразмерной величиной , где к - средняя высота шероховатости, а r- радиус трубы.

В табл. 2 приведены значения  для каждой кривой.

Таблица 2 Значения 

№ кривой		№ кривой	
1 2 3	0,066 0,0328 0,0166	4 5 6	0,00793 0,00397 0,00197

Анализируя кривые Никурадзе, можно прийти к выводу, что гра­фик распадается на пять зон.

Первая зона (Rе<2300, чему соответствует <3,36) - область ламинарного течения. Кривые для труб разной

шероховатости в этой зоне совпадают с прямой I, на которой .

Вторая зона (2300<Rе<4000)- область перехода из ла­минарного режима в турбулентный.

Третья зона (4000<Rе<80 1/) - так называемая область «гладких» труб, в которой к зависит только от числа Рейнольдса Rе и не зависит от шероховатости. Это происходит потому, что при движении жидкости с числом Рейнольдса в пределах третьей зоны выступы шероховатости оказываются погруженными в вязкий под­слой и поэтому, как и в первой зоне, не оказывают влияния на величи­ну коэффициента трения . Как это видно из графика Никурадзе, различные кривые на некотором участке (в пределах третьей зоны) укладываются на одну прямую (прямая II).

Четвертая зона (80 1/ < Rе < 1000 1/) - область шеро­ховатых труб, в ней к зависит как от , так и от Rе.

Пятая зона (Rе> 1000 1/) - квадратичная область, в ко­торой к уже практически не зависит от числа Рейнольдса и является функцией только относительной шероховатости .

С помощью графика Никурадзе легко получить значения коэф­фициентов трения  для труб различной шероховатости. В первой зоне, как уже отмечалось, величина коэффициента трения определяется формулой Пуазейля . Для расчета  в других зонах удобно пользоваться следующими формулами:

во второй зоне (по исследованиям Н. В. Френкеля)

; (87)

в третьей, четвертой и пятой зонах

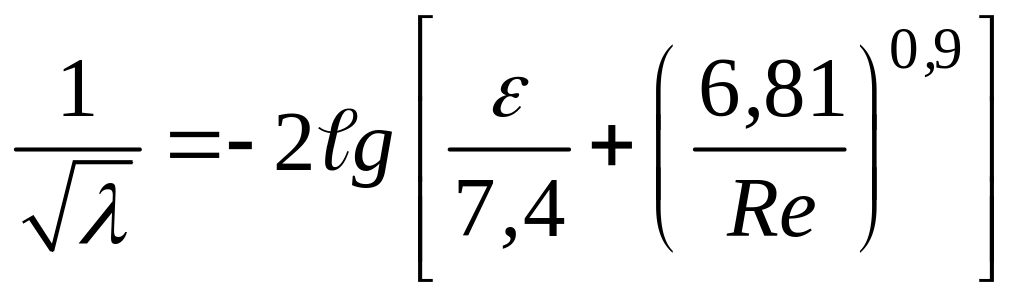(88)

Для области «гладких« труб в равенстве (88) первым слагаемым в квадратных скобках можно пренебречь, а для квадратичной зоны можно пренебречь вторым слагаемым.

Местные потери напора. Местными сопротивлениями на­зывают различные препятствия в трубопроводах - вентили, колена, краны, диффузоры, сужения и расширения.

При протекании жидкости через местные сопротивления возникают области вихревого неупорядоченного движения. На рис.14 эти об­ласти представляются отделенными от основного потока поверхностями раздела. Потери напора на местные сопротивления обуслов­лены большими затратами энергии на внутреннее трение в подобных областях. Для самых разнообразных местных сопротивлений зависи­мость этих потерь от скорости можно считать квадратичной и записать в виде

(89)

где W - средняя скорость потока после местного сопротивления;

 - коэффициент местного сопротивления.

При внезапном расширении потока от сечения F₁ к F₂ коэффициент  можно рассчитать по формуле

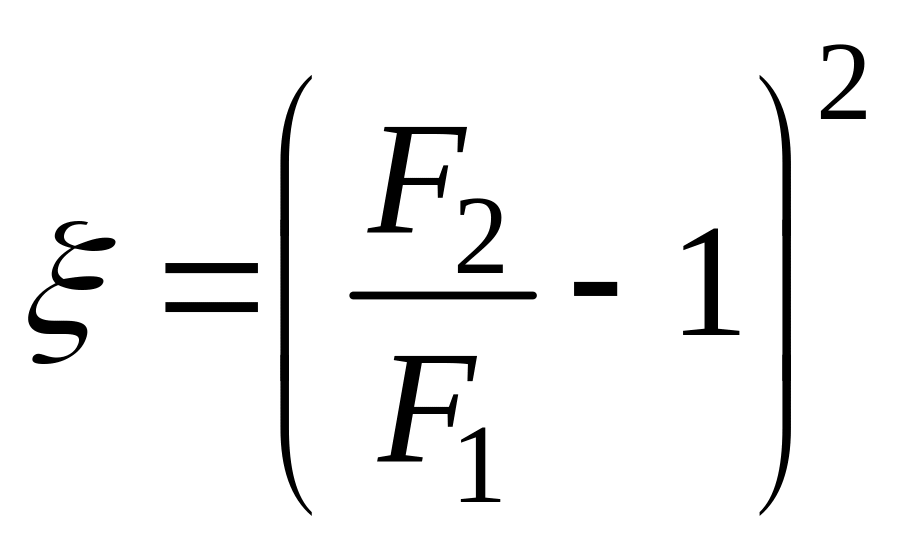
В диффузоре - коническом расширении трубы от сечения F₁ к F₂ - коэффициент местного сопротивления вычисляется по формуле

,

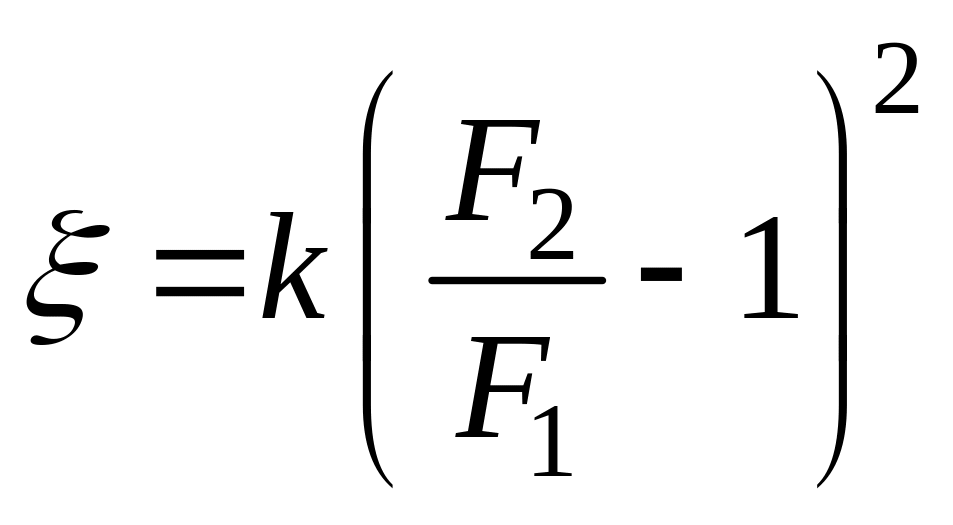где к - экспериментальный коэффициент. Его зависимость от угла раствора конуса 20^о приведена в табл. 3.

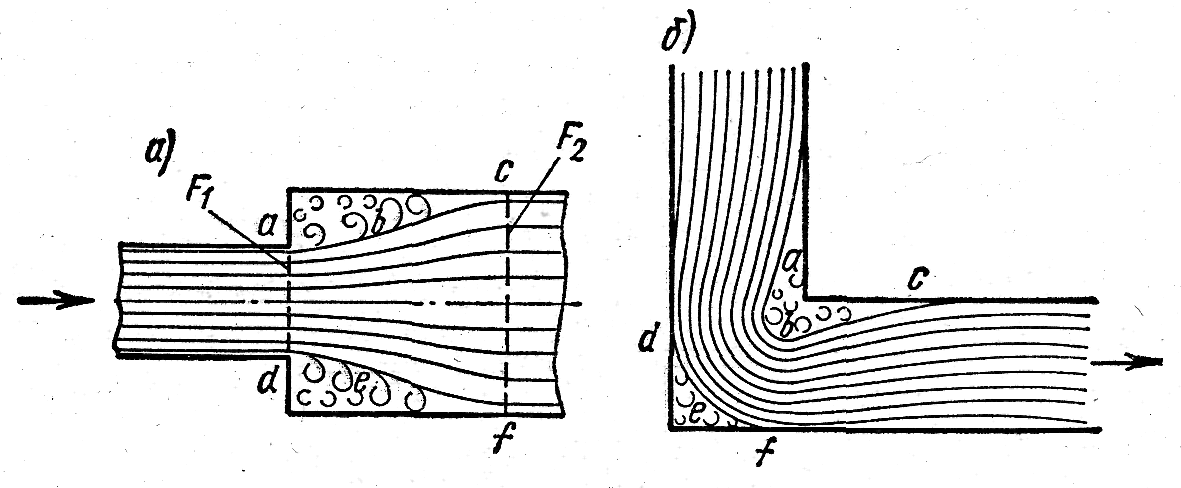
Рис. 14. Местные сопротивления: а) расширение трубы; б) колено

Таблица 3 Экспериментальный коэффициент к

Угол 20о	Коэффициент к	Угол 26°	Коэффициент к
5	0,13	70	1,13
15	0,26	90	1,07
30	0,71	120	1,05
50	1,03	160	1,02

Для закруглений трубопровода с углом поворота ° коэффициент  можно определить по формуле Вейсбаха:

,

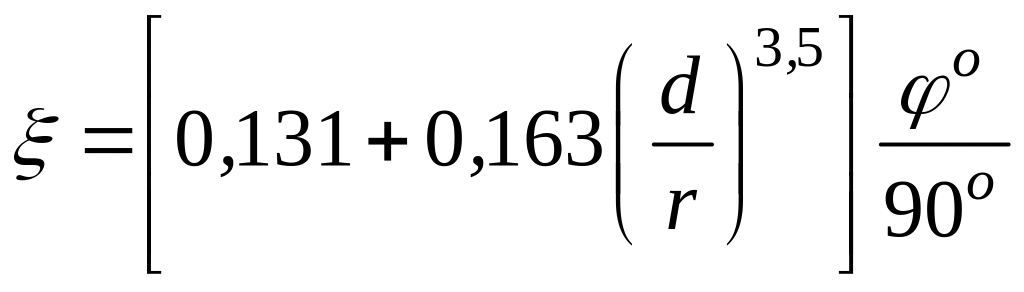где d - диаметр трубы;

r - радиус скругления.

Если в канале на пути потока газа расположены какие-либо пре­пятствия (пучок трубок рекуператора, кирпичная насадка рекуператора, засыпка, представляющая собой слой топлива на колосниковой решетке или слой руды в шахтных печах и др.),то поток газа разбивается в такой насадке или засыпке на ряд более или менее тонких струй, движущихся как бы по каналам неправильной формы. При этом течения отдельных струек могут встречаться, сливаться вместе, а затем опять разделяться. Если в канале более или менее равномерно распо­ложено большое количество препятствий, размеры которых не велики по сравнению с сечением канала, то сопротивление можно считать равномерно распределены по длине канала и коэффициент сопротивления относится к 1 м длины канала в направлении движения потока или к 1 ряду расположенных поперек потока препятствий.

Для расчета сопротивлений засыпок (кускового материала неправильной или правильной формы) можно пользоваться формулой

(90)

где Н – высота слоя, м;

d_э – эффективный диаметр пор ( ), м;

W_от – скорость, условно считаемая по свободному сечению,

м/с;

λ' – коэффициент сопротивления в слое;

d – средний диаметр частиц слоя, м.

Коэффициент сопротивления слоя подсчитывается по формулам :

для ламинарного режима Rе <10 ; (91.а)

для переходного режима 10 < Rе <250 ; (91.б)

для турбулентного режима 250 < Rе <5000 (91.в)

Значение Rе вычисляют по условной скорости, определяемой как отношение расхода к сечению канала, не заполненного засыпкой, т.е.

Эти формулы получены опытным путем и их следует рассматривать, как приближенные, т.к. они получены для определенных условий.