12. Уравнение Бернулли для реальных газов.

Для реальных газов необходимо прежде всего учитывать потери энергии на сопротивление и в связи с этим для элементарной струйки можно записать:

(61)

где - потери энергии на сопротивление струйки по длине dl. Интегрируя это уравнение вдоль элементарной струйки по длине от сечения I до сечения П получим:

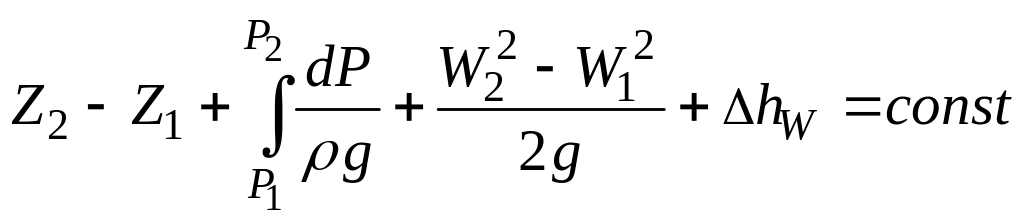(62)

Величину можно найти, если плотность газа является функцией от давления Р. Вид этой функции зависит от характера термодинами­ческого процесса, происходящего в том, или другом случае движения газа. Так ,например, истечение газа из отверстия в резервуаре можно (без существенной погрешности) считать происходящим без обмена теп­ла между выходящим газов и внешней средой, т.е. считать движение адиабатическим. Движение в трубах при известных условиях можно рас­сматривать как изотермическое.

В технической термодинамике имеют важное значение и изучаются следующие термодинамические процессы: изохорный, изобарный, изотерми­ческий , адиабатный. Все процессы являются частными случаями обобщающего политропического процесса.

Из уравнения политропы , находим функцию ρ = f(Р) и она имеет вид:

(63)

После подстановки найдем:

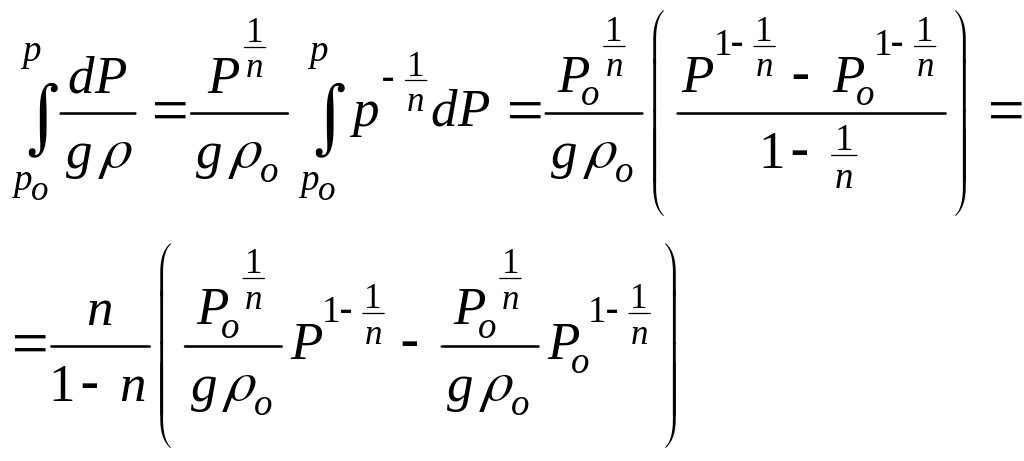
Второе слагаемое в скобках равно:

Первое же слагаемое

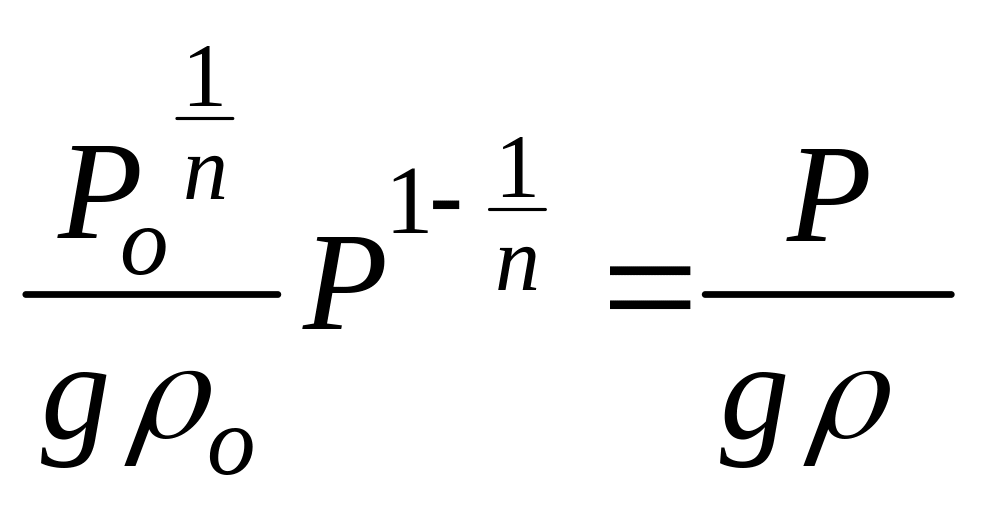
В этом легко убедиться, заметив, что 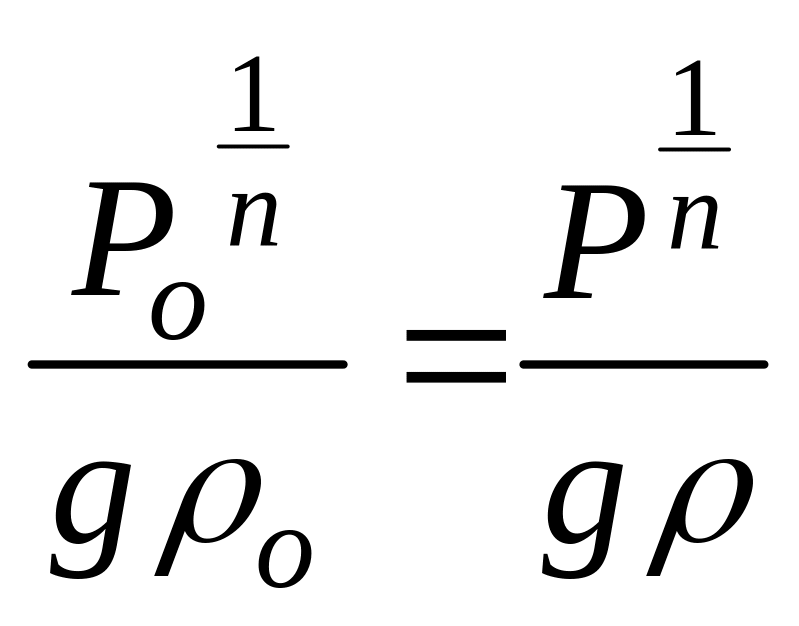в соответствии с уравнением политропы. Таким образом искомая величина интеграла равна

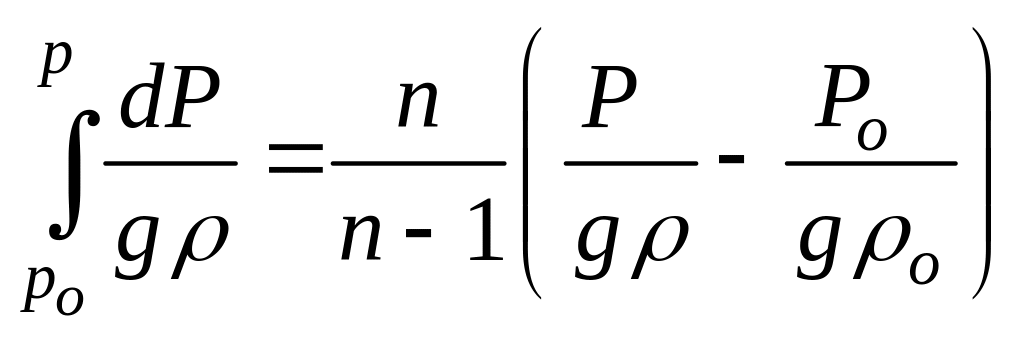(64)

Делаем подстановку в уравнение Бернулли (63) получим

или

(65)

Замечая, что , а можно иначе записать уравнение Бернулли

(66)

Выведенное уравнение носит название обобщенного уравнения Бернулли. Оно выражает скорость движения в функции от давления, плотности газа с учетом производимой газом работы, изменения потенциальной энергии и работы сил трения.

13 Уравнение Бернулли для печных газов.

В уравнение Бернулли (56) входит величина абсолютного дав­ления Р.В печах же обычно измеряют относительное давление, т.е. разность давлений печных газов и окружающей атмосферы. Поэтому уравнение Бернулли для печных газов целесообразно преобразовать так чтобы в него входили разности давлений.

Для этой цели напишем уравнение Бернулли для газов, движущих­ся по каналу для двух сечений (рис.9) и для покоящегося атмосфер­ного воздуха, окружающего канал, почленно одного из од­ного другого.

- печные газы (67.а)

- атмосферный воздух (67.б)

Вычтем из первого уравнения второе

(68)

Рис. 9 К выводу уравнения Бернулли для печных газов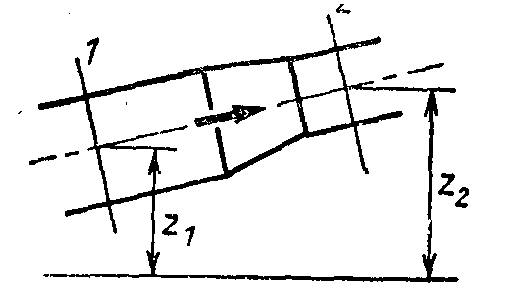

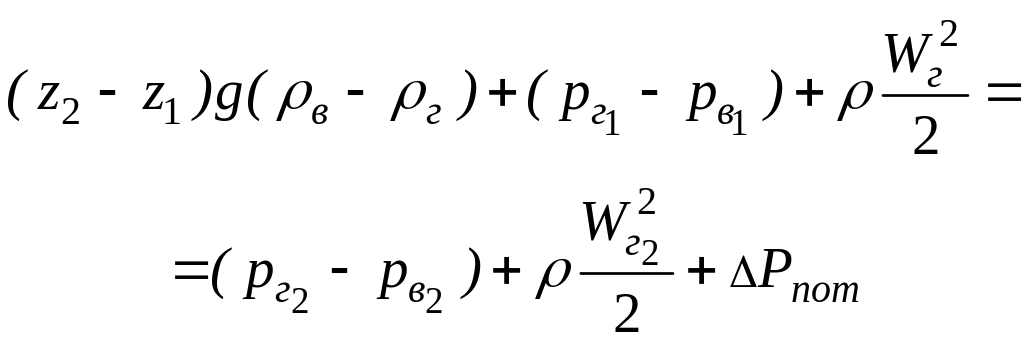С точки зрения энергии каждую часть последнего уравнения можно рас­сматривать как энергию 1 м³ газа относительно 1 м³ окружающего воз­духа и последнее уравнение для практических расчетов может быть переписано в следующем виде:

(69)

Обозначив в последнем уравнении

Получим основное уравнение Бернулли для печных газов

(70)

Величина q называют геометрическим давлением.

Выведенные выше уравнения Бернулли относятся к бесконечно малой струйке жидкости, где скорости по сечению каждой были равны, В потоке газа конечного поперечного сечения наблюдается неравномер­ное распределение скорости,

С учетом средней скорости и коэффициента Кориолиса можно уравнение (69) записать для потока газа

(71)