
- •Оглавление
- •Предисловие
- •1. Теплопроводность
- •1.1 Основной закон теплопроводности
- •Стационарная теплопроводность плоской стенки
- •Однородная стенка
- •1.2.2. Многослойная стенка
- •Стационарная теплопроводность цилиндрической стенки
- •Однородная стенка
- •1.3. 2 Многослойная стенка
- •1.3. 3 Упрощение расчетных формул (дополнительные сведения)
- •Стационарная теплопроводность шаровой стенки (дополнительные сведения)
- •Стационарная теплопроводность тел неправильной формы
- •1.6 Нестационарная теплопроводность
- •1.6.1 Общие понятия
- •1.6.2 Нагрев тел с равномерным температурным полем – «термически тонких тел»
- •1.6.2.1 Тепло на поверхность передается конвекцией.
- •1.6.3. Нагрев тел с неравномерным температурным полем. (термически массивных тел)
- •1.6.3.1 Нагрев при постоянной температуре поверхности
- •1.6.3. 2 Нагрев при постоянной плотности теплового потока через поверхность
- •1.6.3.3 Нагрев при передаче тепла конвекцией от среды с постоянной температурой
- •2 Конвективный теплообмен
- •2.1. Основные положения конвективного теплообмена
- •2. 2. Пограничный слой и уравнение теплообмена на границе раздела
- •2. 3. Дифференциальное уравнение теплопередачи конвекцией
- •2.4 Подобие и моделирование процессов конвективного теплообмена
- •2. 5 Моделирование процессов конвективного теплообмена
- •2. 6 Физический смысл критериев теплового подобия
- •2.7 Теплопередача конвекцией при свободном движении
- •2. 8 Теплопередача конвекцией в вынужденном потоке
- •2. 9 Теплообмен при продольном обтекании плиты, прямоугольного параллелепипеда
- •2.10 Значение теплопередачи конвекцией в нагревательных печах
- •3 Лучистый теплообмен
- •3.1 Общие положения
- •3.2 Основные понятия
- •3.3 Законы теплового излучения для условия равновесной среды
- •3.4 Лучистый теплообмен между двумя серыми телами
- •3.4.1 Две небольшие и далекие поверхности
- •3.4.2 Лучистый теплообмен между двумя телами,
- •3.5 Лучистый теплообмен в замкнутой системе тел
- •3.6 Теплообмен излучением при установке экранов
- •3.7 Излучение через отверстие в печных стенах
- •3.8 Теплообмен между газами и твердыми телами
- •3.8.1 Особенности излучения газов и паров
- •3.8.2 Уравнение переноса лучистой энергии
- •3.9 Лучистый теплообмен между газом и окружающими его стенками
- •3.10 Излучение факела пламени и карбюрация
- •3.11 Лучистый теплообмен одновременно с конвекцией
- •Перечень ссылок
1.6.3. Нагрев тел с неравномерным температурным полем. (термически массивных тел)
Температурное поле при нагреве и охлаждении является нерав-номерным. Если поместить стальной слиток в нагретую печь, то сначала температура его наружных слоев будет повышаться быстрее, а внутренних медленнее - возникнет неравномерность распределения температуры. Через некоторое время положение изменится: внутренние слои будут нагреваться быстрее - температура начнет выравниваться.
Температурное поле в слитке, как и в других телах, являющееся функцией времени и координат, описывается дифференциальным уравнением теплопроводности Фурье
![]() (56)
(56)
Величина λ/ср = а называется коэффициентом температуропроводности и характеризует теплоинерционные свойства тела: чем выше λ, тем быстрее повышается температура при нагреве; чем больше объемная теплоемкость (сρ), тем медленнее идет повышение температуры.
Чтобы найти температурное поле t = t(х,у,z,τ) в любой момент времени, т. е. чтобы решить уравнение (56), надо знать распределение температуры в начальный момент (начальное условие), геометрическую форму тела и закон теплового взаимодействия между окружающей средой и поверхностью тела (граничное условие). Совокупность начального и граничного условий называют краевыми условиями.
Граничное условие можно сформулировать различными способами. Целесообразность того или другого способа определяется конкретными условиями нагрева или охлаждения: в одном случае легко задать температуру тела, в другом - тепловой поток, в третьем проще задать температуру среды. Различные виды граничных условий сформулированы ниже.
1.6.3.1 Нагрев при постоянной температуре поверхности
Задание температуры поверхности тела в функции времени и координат tпов = t(х,у,z,τ) называется граничным условием I рода. Рассмотрим случай, для которого существует аналитическое решение: бесконечная пластина, у которой в начальный момент поле температур равномерное; температура на наружных поверхностях мгновенно поднимается до одинаковой величины и в дальнейшем остается постоянной tпов =сопst.
Нагрев пластины протекает так, как показано на рис.15 . Температура центра пластины в начале нагрева поднимается медленно, затем быстрее и, по мере выравнивания температуры, замедляется снова. Видно (см. правую часть рисунка), что температурный градиент на поверхности пластины с течением времени уменьшается, поэтому тепловой поток q, проходящий через поверхность, уменьшается.
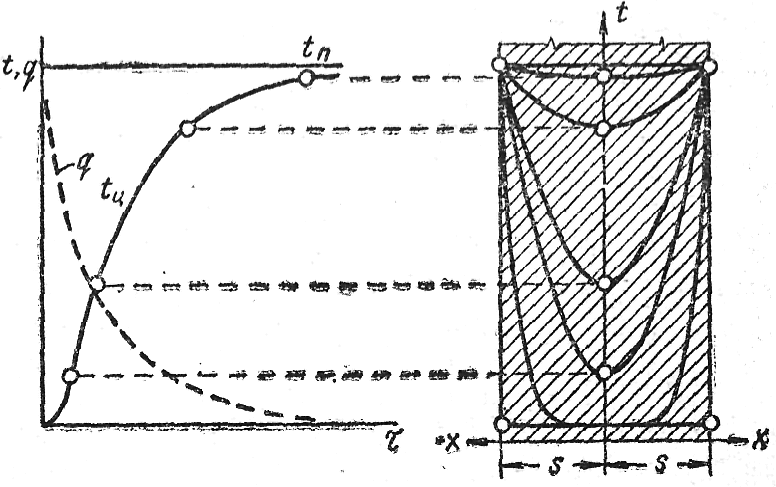
Рис. 15 Нагрев пластины при постоянной температуре
Поверхности ( граничные условия I рода)
1.6.3. 2 Нагрев при постоянной плотности теплового потока через поверхность
Задание плотности теплового потока, проходящего через поверхность тела, в функции времени и координат qпов =q(х,у,z,τ) называется граничным условием II рода. Рассмотрим наиболее простой случай, когда нагревается бесконечная пластина, причем плотность теплового потока, проходящего через ограничивающие ее поверхности, не изменяется с течением времени. До начала нагрева температурное поле пластины равномерное. Нагрев при q = сопst встречается в методических, камерных печах, нагревательных колодцах.
Нагрев пластины протекает так, как показано на рис.16 . Температурный градиент на поверхности, естественно, сохраняет постоянное значение в течение всего времени нагрева. Вскоре после начала нагрева температура во всех точках тела начинает изменяться с течением времени по линейному закону, а распределение температуры следует закону параболы.
