1.6 Нестационарная теплопроводность

1.6.1 Общие понятия

Теплопроводность называется нестационарной, если темпера­турное поле с течением времени изменяется, т. е. происходит на­грев или охлаждение тела.

Основное содержание задач нестационарной теплопровод­ности - отыскание распределения температуры в твердых телах в заданные моменты времени. Все выведенные ниже формулы спра­ведливы как для нагрева, так и для охлаждения тел.

Для того, чтобы воспользоваться формулами нестационарной теплопроводности для расчета процесса нагрева или охлаждения необходимо принять по какой модели идет этот процесс – по модели нагрева термически тонкого или термически массивного тела. Для этого рассмотрим критерий Био в формуле термических сопротивлений

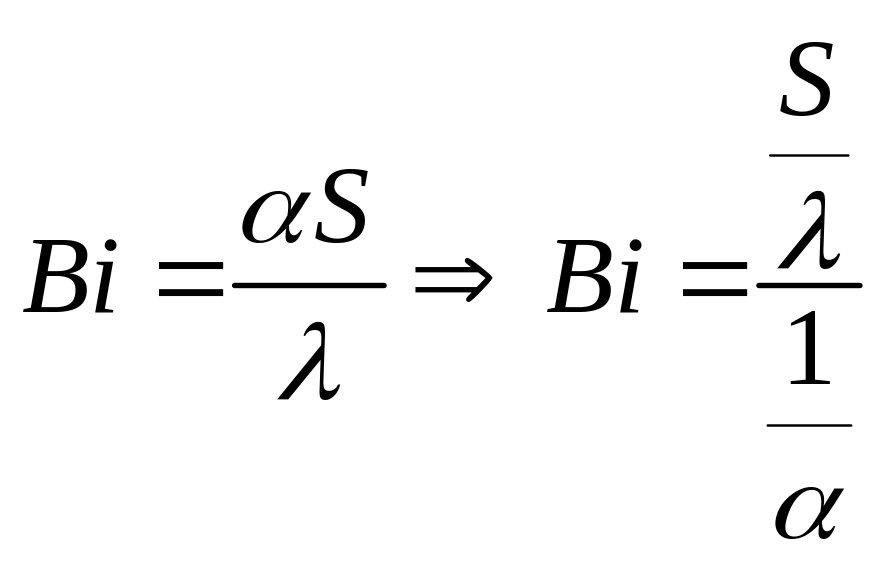(47)

где α – коэффициент теплоотдачи, Вт/м² К;

S – тепловая толщина, м;

 – коэффициент теплопроводности материала, Вт/м К.

В соответствии с приведенной зависимостью критерий Био представляет собой отношение внутреннего теплового сопротивления к внешнему . Чем больше критерий Био, тем больше интенсивность внешнего теплообмена по сравнению с интенсивностью внутреннего. В связи с этим большим значением критерия Био должна соответствовать меньшая равномерность распределения температур в объеме тела, а соответственно большая разница температур, например, между поверхностью и центром заготовки. И наоборот, чем меньше величина критерия Био, тем равномернее распределение температуры в объеме тела на протяжении всего периода нагрева (охлаждения).

Тела, которые нагреваются (охлаждаются) равномерно по всему объему или разностью температур (например, между поверхностью и центом можно пренебречь), называют термическим тонкими телами, а критерий Вi ≤ 0,25

Тела, для которых критерий Вi ≥ 0,5 и которые нагреваются неравномерно и для которых разностью температур (например, между поверхностью и центом) пренебречь нельзя, называются термически массивными телами.

Таким образом, для решения вопроса каким методом проводить расчет нагрева (охлаждения) тела, необходимо вначале вычислить по имеющимся данным критерий Био. Если Вi > 0,5, то расчет необходимо вести по методике термически массивного тела. Если Вi < 0,25, то расчет необходимо вести по методике термически тонкого тела, а так же с использованием критериев.

Если Вi находится между 0,25 и 0,5, то такие тема называются телами тяготеющими к термически тонким и ли термически массивным телам. Таким образом, методику расчета принимают исходя из технологических рекомендаций.

1.6.2 Нагрев тел с равномерным температурным полем – «термически тонких тел»

Рассмотрим простейший случай нагрева, когда температура во всех точках нагреваемого тела одинакова, т. е. не является функ­цией координат.

Рассмотрим два варианта нагрева термически тонких тел: 1) тепло передается конвекцией; 2) тепло передается излучением. При этом сохраняется условие Вi < 0,25.

1.6.2.1 Тепло на поверхность передается конвекцией.

Составим уравне­ние теплового баланса тела за время dτ. Согласно формуле (Ньютона-Рихмана), количество тепла, проходящего через поверхность тела, в резуль­тате теплоотдачи α окружающей среды (t_с) составит

(48)

Это тепло пойдет на увеличение энтальпии тела массой М_с и удельной теплоемкостью «с»: . Приравняв и dQ, разделив переменные и проинтегрировав от начального момента времени (τ = 0), когда t= t_н, до момента времени τ, получим:

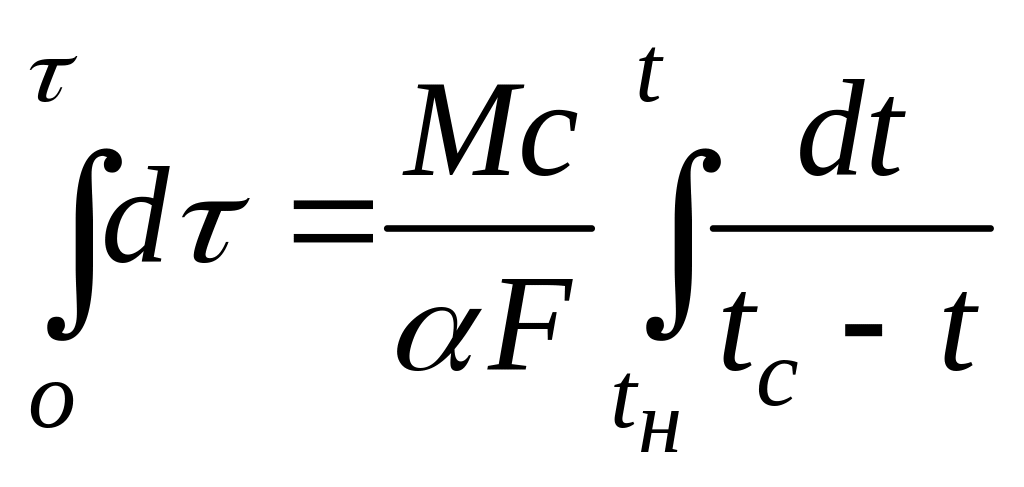(49)

(50)

Уравнение (50) позволяет рассчитать время, необходимое для нагрева тела от t_и до t. Для расчета температуры, которую приобретает тело за время τ после начала нагрева, формулу (1-50) следует преобразовать:

(51)

1.6.2.2 Тепло на поверхность передается излучением. Задача анало­гична предыдущей, но для расчета тепла dQ*, проходящего через поверхность тела за время dτ, применяют формулу лучистого теплообмена.

Из условия dQ* = dН

(52)

Разделив переменные и проинтегрировав уравнение (207),

Получим

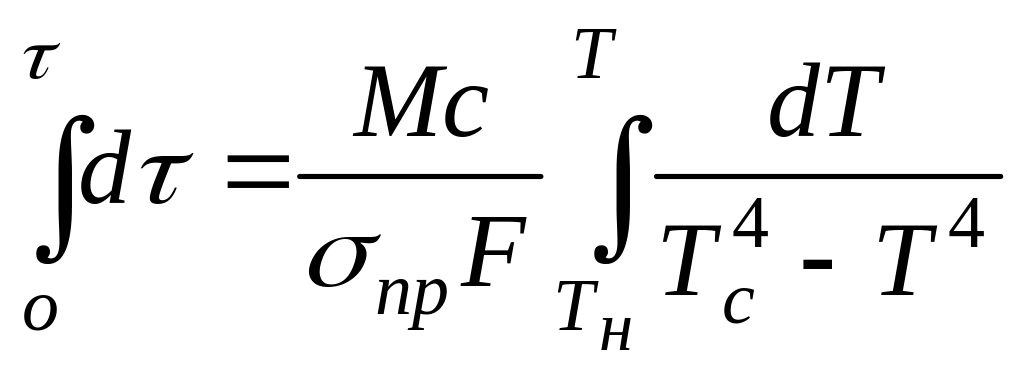(53)

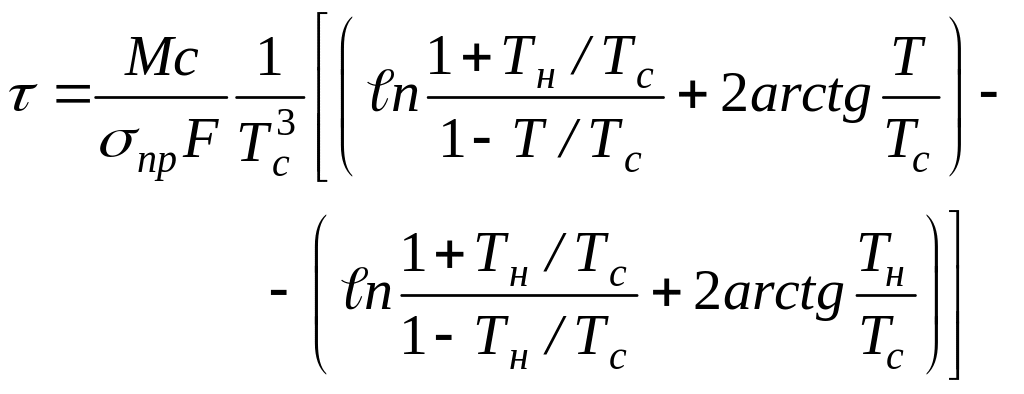(54)

Выражение (54) называется фор­мулой Старка. В этой формуле члены в круглых скобках представляют собой одинаковые функции отношения темпе­ратур, поэтому ее можно записать так:

(55)

Значения функции ф приведены на рис. 14.

Рис. 14 Значение функции

ψ (Т/Т_с)

С помощью формулы (55) и рис. 14 можно решить и обратную задачу.