2. Стационарная теплопроводность шаровой стенки (дополнительные сведения)

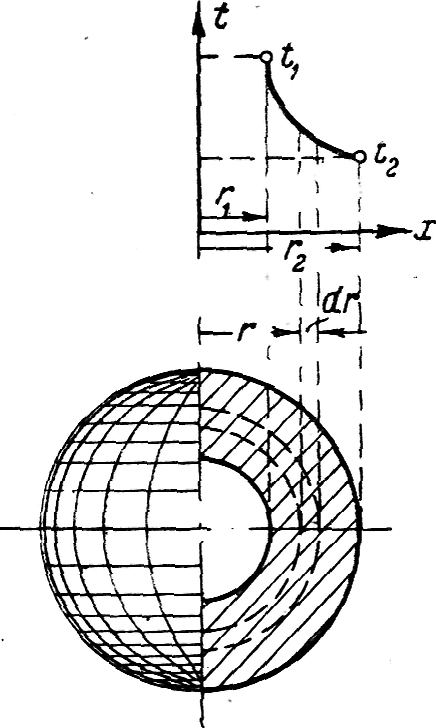
Пусть имеется полый шар, радиус внутренней поверхности которого равен r₁ и внешней r₂. Стенка шара состоит из одного материала, коэффициент теплопроводности которого по-

стоянен и равен λ. Внутренняя и внешняя поверхности шара поддерживаются при постоянных температурах t₁ и t₂, причем

t₁ > t₂. (рис.13). Температура изменяется только в направ­лении радиуса. Изотермические поверхности представляют собой концентрические шаровые поверхности.

Выделим внутри стенки шаровой слой радиусом г и тол­щиной dr. Поверхность этого слоя является изотермиче­ской.

Согласно закону Фурье тепловой поток, проходящее через этот слой равен

Рис.1-14. Однородная шаровая стенка.

(41а)

Разделив переменные, получим:

(41в)

Интегрирование этого уравнения дает:

(41с)

Подставляя в уравнение (41с) значения переменных величин на границах стен­ки, а именно при r = r₁, t = t₁, и при r = r₂, t = t₂, получим два равенства:

откуда определяется искомая величина

(41д)

(41е)

Вычитая из первого равенства (41д) второе (41е), получим

Откуда определяется искомая величина q

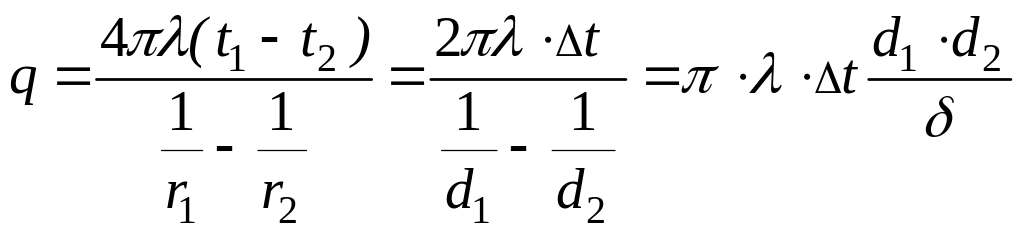(42)

где δ - толщина стенки, равная .

Эти уравнения являются расчетными формулами теплопро­водности шаровой стенки.

Если в уравнение (41с) подставить значение С из уравне­ния (41д) и значение q из уравнения (42), то получим уравнение температурной кривой:

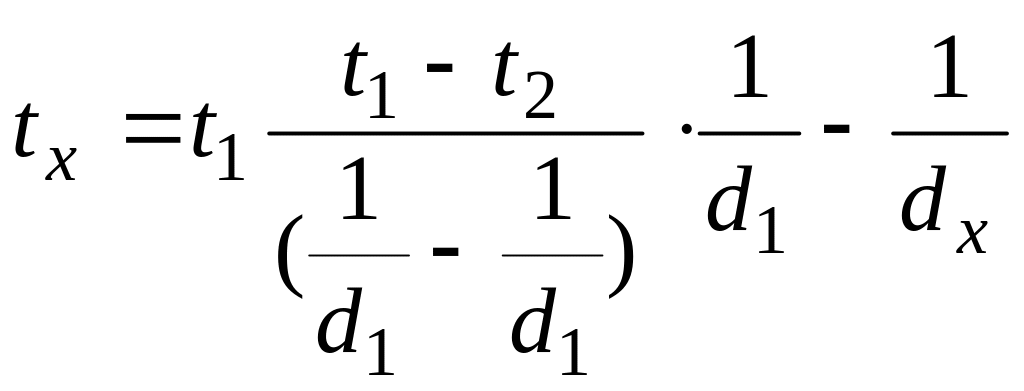(43)

Последнее представляет собой уравнение гиперболы. Сле­довательно, при постоянном значении коэффициента тепло­проводности внутри однородной шаровой стенки температура изменяется по закону гиперболы.

Если же учесть зависимость коэффициента теплопровод­ности от температуры λ = λ₀(1+ bt),, то уравнение температур­ной кривой для сферической стенки будет иметь следующий вид:

2. Стационарная теплопроводность тел неправильной формы

Каждая из вышеприведенных формул (12а), (26) и (42) применима лишь для одного вида геометрически правильного тела - плоского, цилиндрического или шарового. Расчет тепло-проводности всех этих тел можно охватить одной формулой теплового потока , которая имеет следующий вид:

, Вт (44)

где λ - коэффициент теплопроводности;

δ - толщина стенки;

Δt - температурный напор;

F_х - расчетная поверхность тела.

В зависимости от формы тела F_х определяется различно; если F₁ - внутренняя и F ₂ — внешняя поверхность тела, то: а) для плоской стенки и цилиндрической при < 2

(45а)

б) для цилиндрической стенки при >2

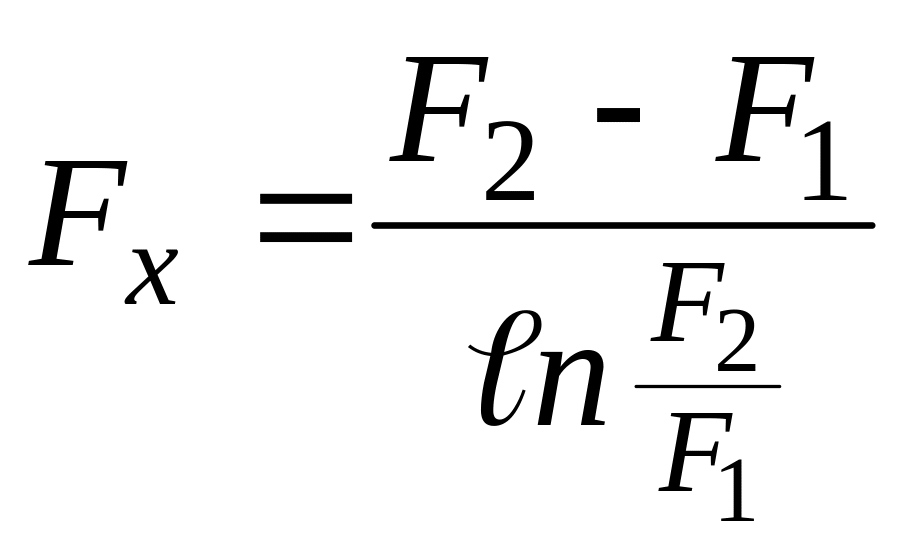(45в)

в) для шаровой стенки

(45с)

При расчете теплопроводности плоской стенки, цилиндра и шара формула (44) перед формулами (12), (26) и (42) никаких преимуществ не имеет. Однако ее достоинство заклю­чается в том, что по ней можно рассчитать теплопроводность тел неправильной геометрической формы, например теплопровод­ность плоской стенки, у которой F₁ ≠ F₁ т. е. когда поперечное сечение теплового потока в ней представляет собой переменную величину; теплопроводность любых цилиндрических сечений, ограниченных плавными кривыми; теплопроводность всяких замкнутых тел, у которых все три линейных размера между собой близки.

В практике нередко встречаются случаи, когда объект расче­та является сложным сочетанием различных тел. Расчет теплопроводности таких сложных объек­тов обычно производят раздельно по элементам, мысленно разре­зая их плоскостями параллельно и перпендикулярно направле­нию теплового потока. Однако вследствие различия термических сопротивлений отдельных элементов, а также вследствие разли­чия их формы в местах соединения элементов распределение температур может иметь очень сложный характер и направление теплового потока может оказаться неожиданным. Поэтому указанный способ расчета сложных объектов имеет лишь прибли­женный характер. Более точно расчеты сложных объектов можно провести лишь в том случае, если известно распределение изо­терм и линий тока, которое можно определить опытным путем при помощи методов гидроэлектроаналогии. Однако самые на­дежные данные по теплопроводности сложных объектов можно получить только путем непосредственного эксперимента. Опыт можно проводить или на самом объекте, или на уменьшенной модели этого объекта.

При выводе расчетных формул принималось, что температуры поверхностей тела постоянны. В практических расчетах это усло­вие не всегда удовлетворяется. В таких случаях поступают сле­дующим образом. Если в отдельных точках поверхности темпера­тура разнится не сильно, то производят усреднение температур по поверхности. В дальнейшем с этой средней температурой рас­чет производится как с постоянной. Средняя температура по по­верхности определяется по формуле

(46)

где F_1, F_2, ^{. . .} , F_п - участки поверхности с постоянной тем­пе-

ратурой;

t_1, t₂, ^{. . .} , t_п - температуры этих участков.

Если же температура по поверхности изменяется резко, тогда поверхность разбивается на участки и для каждого из них в от­дельности подсчитывается количество прошедшего тепла. Скла­дывая эти количества и деля сумму на общую поверхность тела, получают среднее значение теплового потока. В пределах каждо­го участка усреднение температуры производят по формуле (46).

Теплопроводность жидкостных и газовых тел определяется по тем же формулам, какие были приведены для твердых тел. Однако при этом необходимо иметь в виду, что в жидкостях и газах в чистом виде явление теплопроводностди наблюдается лишь в очень тонких слоях и при таком расположении слоя, ког­да частицы с наименьшей плотностью, т. е. наиболее нагретые, находятся наверху, а наиболее плотные - внизу. В противном случае в слое возникает конвекция, вследствие чего передача тепла через жидкостный или газовый слой возрастает. Кроме того, через газовые слои тепло передается не только путем теп­лопроводности, но и путем излучения. Все эти обстоятельства сильно затрудняют расчет теплопроводности через газы, и ошиб­ка расчета может достигать 50 - 200%. Поэтому при расчете теплопередачи через газовые прослойки необходимо принимать во внимание и влияние конвекции и излучения.