1.3. 2 Многослойная стенка

Пусть цилиндрическая стенка состоит из нескольких, например трех, разнородных слоев. Благодаря хорошему контакту между слоями соприкасающиеся поверхности разных слоев имеют общую температуру. Диа­метры и коэффициенты теплопроводности отдельных слоев известны, их обозначения см. на рис.11. Кроме того, из­вестны температуры внутренней и внешней поверхностей многослойной стенки t₁ и t₄. В местах соприкоснове­ния слоев температуры неизвестны, обозначим их через t₂ и t₃

При стационарном режиме количе­ство тепла, проходящего через каждый слой, одинаково и постоянно. Поэтому на основании формулы (29) можно написать плотность теплового потока

(32)

Из этих уравнений определяется изменение температуры в каждом слое:

(33)

Сумма изменений температуры в каждом слое составляет полный температурный напор. Складывая отдельно левые и правые части системы уравнений (в), получаем:

(34)

откуда определяется значение теплового потока q_l.

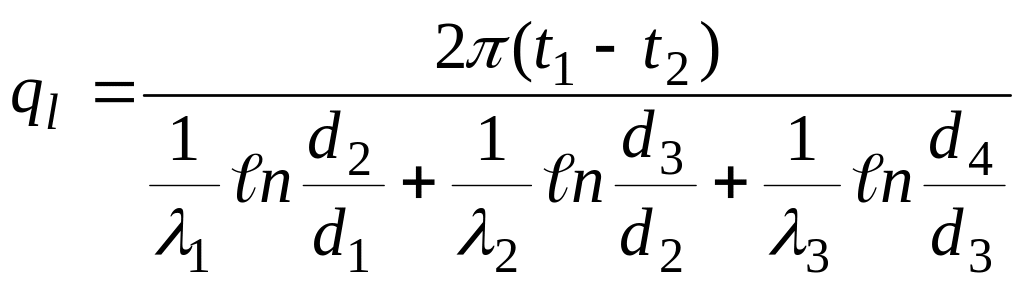(35)

По аналогии с этим без вывода можно написать формулу для п-слойной стенки:

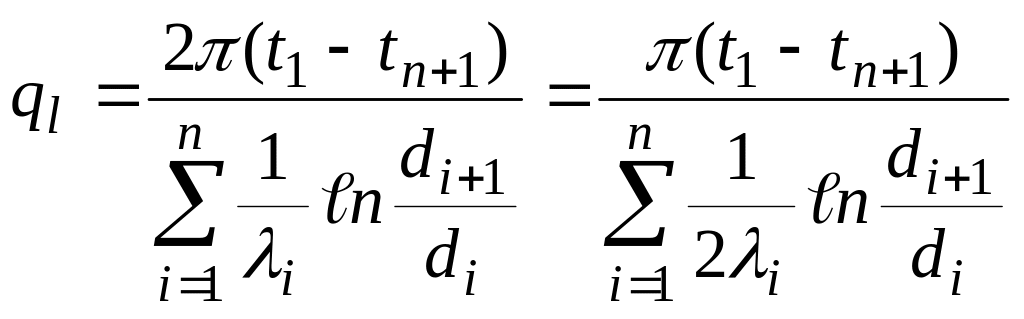(36)

Если значение q_l из формулы (36) подставить в уравне­ние (33), то получим значения неизвестных температур на поверхности соприкосновения слоев:

(37)

Внутри каждого слоя согласно уравнению (27) темпера­тура изменяется по логарифмическому закону, но для много­слойной стенки в целом температурная кривая представляет собой ломаную кривую (рис.11).

1.3. 3 Упрощение расчетных формул (дополнительные сведения)

Приведенные выше рас­четные формулы для трубы неудобны тем, что в них входит логарифм. С целью упрощения расчетов вместо формулы (29) может быть применена следующая формула теплового потока

или плотности теплового потока

(38)

аналогичная формуле для плоской стенки.

Здесь средний диаметр трубы и -

толщина стенки трубы. Влияние кривизны стенки при этом учитывается особым коэффициентом φ, который называется коэффициентом кривизны. Его значение определяется отношением диаметров ; в самом деле, из сопоставления между собой формул (29) и (38) имеем:

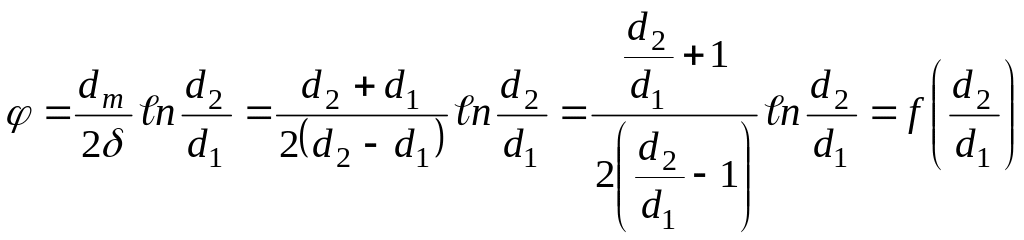(39)

Значения коэффици­ента кривизны для различных отношений приведены на рис. 12.

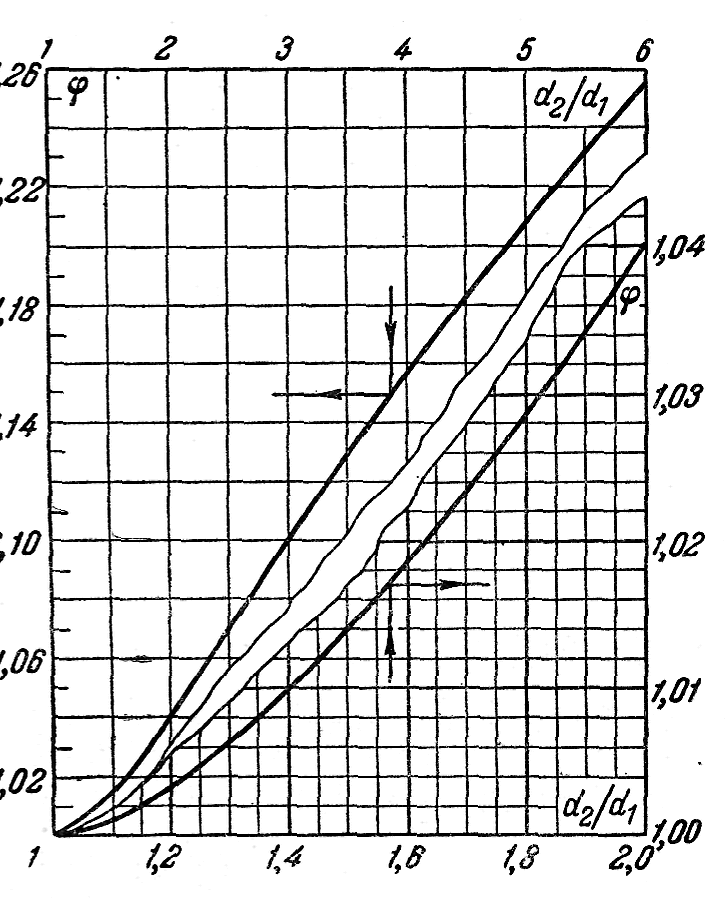
Рис. 12

приведены на рис.12. Из фигуры видно, что при <2 значение φ близко к единице. Так как при φ=1 формула (38) тождественна формуле (12), то это означает, что если толщина стенки трубы по сравнению с диаметром мала или, что то же, если отношение мало, то влиянием кри­визны стенки можно пренебречь, и тогда рас­чет теплопроводности трубы производится по формулам для плоской стенки.

При расчете теплопроводности многослойной стенки трубы вместо формулы (36) также можно применять упрощенную, которая в этом случае имеет следующий вид:

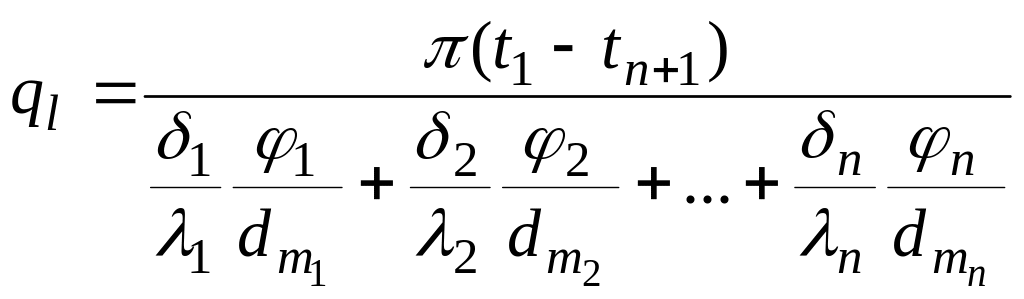, (40)

где δ_i - толщина;

d_тп - средний диаметр;

λ - коэффициент теплопроводности;

φ - коэффициент кривизны отдельных слоев много-

слой­ной стенки трубы.