2. Стационарная теплопроводность цилиндрической стенки

1. Однородная стенка

Рис.10 Однородная цилиндрическая стенка

Рассмотрим однородную цилиндри­ческую стенку (трубу) длиной l м, с внутренним радиусом r₁ и внешним r₂. Коэффициент теплопроводности материала постоянен и равен λ. Внутренняя и внешняя поверхности под­держиваются при постоянных температурах t₁ и t₂, причем t₁ > t₂, (рис.10). Температура изменяется только в радиаль­ном направлении х. Следовательно, температурное поле здесь будет одномерным, а изотермические поверхности цилиндри­ческими поверхностями, имеющими с трубой общую ось. Вы­делим внутри стенки кольцевой слой с радиусом r и толщи­ной dr, ограниченный изотермическими поверхностями. Согласно закону Фурье тепловой поток, проходящий через этот слой в сек, равен (Вт)

(25а)

Разделив переменные, получим

(25в)

Интегрирование последнего уравнения

дает: (25с)

Подставляя значение переменных на границах стенки, а именно при r = r₁ и t = t₁ при r = r₂ и t = t₂, получаем следующие два равенства:

(25д)

(25е)

Вычитая из первого равенства (д) второе (е), находим:

откуда определяется неизвестная величина q :

(26)

Следовательно, тепловой поток через стенку трубы, пря- мо пропорционально коэффициенту теплопроводности λ, длине l и температурному напору Δt = (t₁ - t₂₎ и обратно пропорционально натуральному логарифму отношения внешнего радиуса трубы r₂ к внутреннему r₁. Вместо отношения радиусов можно брать отношение диаметров.

Уравнение (26) является расчетной формулой теплопроводности цилиндрической стенки. Оно остается справедливым для случая, когда t₁ < t₂, т.е. когда тепловой поток направлен от наружной поверхности к внутренней. Если в уравнение (с) подставить значение постоянной С уравнения (д), а значение Q из уравнения (26), то получим ­уравнение температурной кривой:

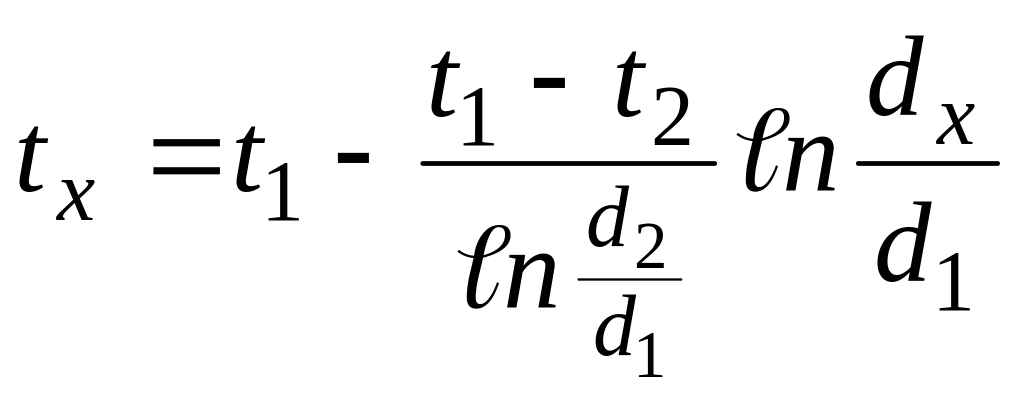, ^оС (27)

Оно представляет собой уравнение логарифмической кривой. Следовательно, внутри однородной цилиндрической стенки постоянном значении коэффициента теплопроводности температура изменяется по логарифмической кривой (рис.10). Дополнительные сведения. Если учесть зависимость коэффициента теплопроводности от температуры λ = λ₀(1+ bt), то уравнение температурной кривой для цилиндрической стенки будет иметь следующий вид:

(28)

Количество тепла, проходящее в час через стенку трубы, может быть отнесено либо к 1 пог. м длины трубопровода, либо к единице внутренней, либо к единице внешней поверхности трубы. При этом расчетные формулы соответственно принимают следующий вид:

, Вт/м (29)

, Вт/м² (30)

, Вт/м² (31)

Рис. 11 Многослойная цилиндрическая стенка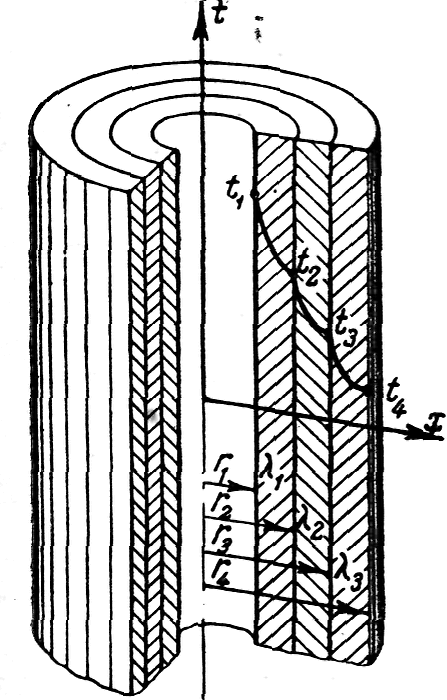

Так как внутренняя и внешняя поверхности трубы по величине различны, то различными получаются и значения удельных тепловых потоков q₁ и q_2. Из формул (1.17), (1.18) и (1.19) легко полу-чить соотношение, связывающее между со­бой величины q₁ и q₂ и q_l, а именно:

q ·l= π d₁· q₁ = π d₂· q₂