1.2.2. Многослойная стенка

Стенки, состоящие из нескольких разнородных слоев, называются многослойными. Именно такой является кладка металлургических печей, состоящая из огнеупорного и теплоизоляционного материала, а так же обмуровка теплоэнергетических агрегатов.

Пусть стенка состоит из нескольких, например трех, разных, но плотно прилегающих друг к другу слоев (рис.7). Толщина первого слоя равна δ_1, второго δ₂ и третьего δ₃ Соответственно коэффициенты теплопроводности слое λ_1, λ₂ и λ₃. Кроме того, известны температуры наружных поверхностей многослойной стенки t₁ и t₂. Благодаря хорошему контакту между слоями соприкасающиеся поверхности имеют одну и ту же температуру, но значения этих температур неизвестны; обозначим их через t₂ и t₃

При стационарном режиме плотность теплового потока постоянна и для всех слоев одинакова. Поэтому на основании формулы (12) для каждого слоя можно написать плотность теплового потока:

Рис.7 Многослойная плоская стенк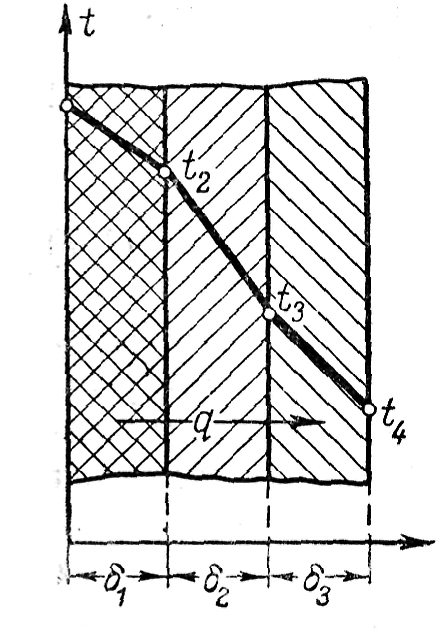а.

(18а)

Из этих уравнений легко определить изменение температуры в каждом слое:

(18в)

Сумма изменений температур в каждом слое составляет полный температурный напор. Складывая левые и правые части системы уравнений (в), получим:

(18с)

Из этого соотношения определяется значение плот-ности теплового потока:

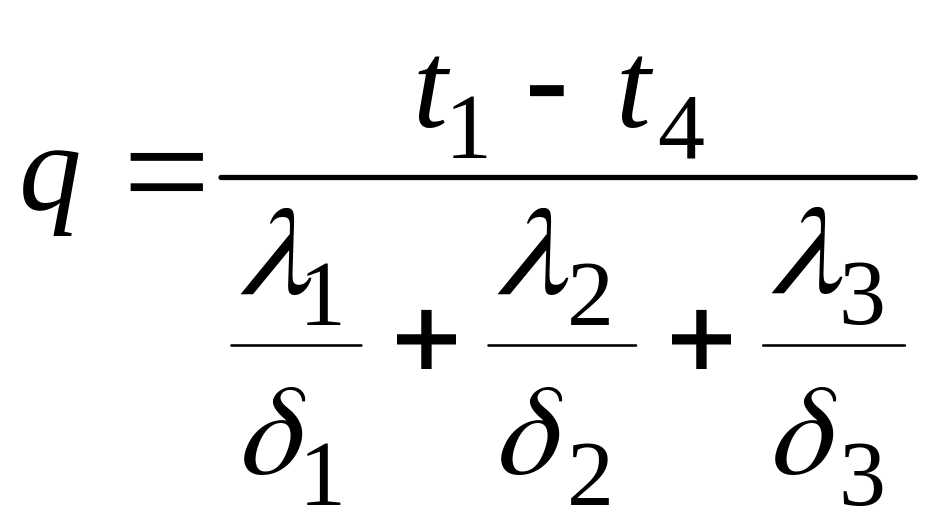(19)

По аналогии можно сразу записать расчетную формулу для п-слойной стенки:

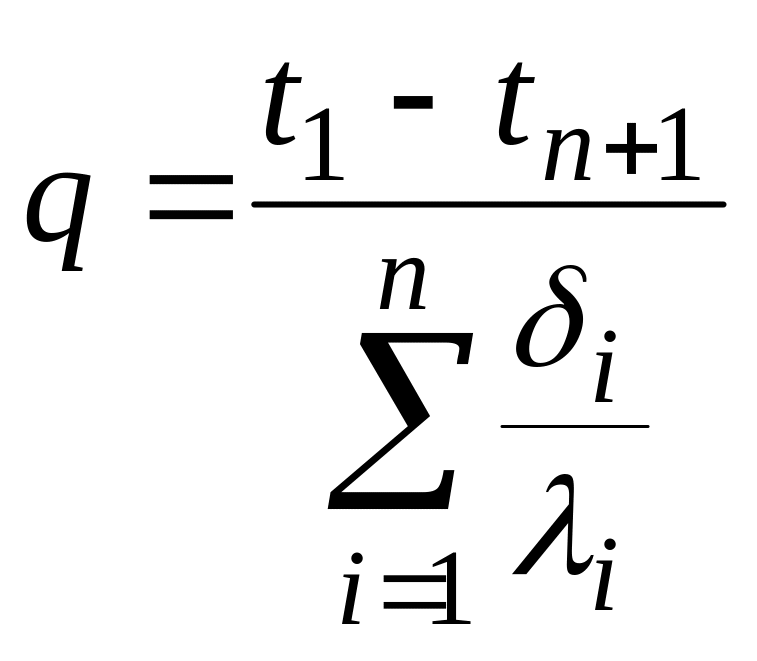(20)

Так как каждое слагаемое знаменателя в уравнении (19) представляет собой термиче­ское сопротивление слоя, то из уравнения следует, что общее термическое сопротивлением многослойной стенки равно сум­ме частных термических сопро­тивлений. Если значение теплового потока из формулы (19) подставить в уравнения (18в), то получим значения неизвестных температур t₂ и t₃

Внутри каждого слоя температурная кривая изменяется по прямой, но для многослойной стенки в целом она пред­ставляет собой ломаную линию (рис.8).

Рис. 8 Графический способ определения промежуточных температур t₁ и t₂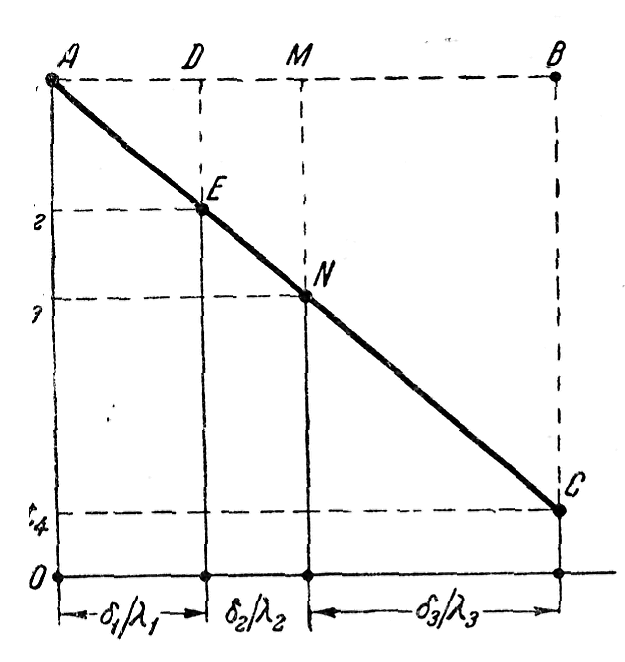

Дополнительные сведения. Значения неизвестных температур t₂ и t₃ можно опреде­лить графически.

При этом построение графика производится следующим образом. По оси абсцисс (рис.8) в любом мас­штабе, но в порядке расположения слоев откладываются зна­чения их термических сопротивлений

и восстанав­ливают-ся перпендикуляры. На крайних из них также в произ­вольном, но одинаковом масштабе откладываются значения наружных температур t₁ и t₄. Полученные точки А и С соединяются прямой. Точки пересечения этой прямой со ними перпендикулярами дают значения искомых температур t₂ и t₃. В самом деле, ΔАВС ΔАВЕ. Следовательно,

Подставляя значения отрезков, получаем:

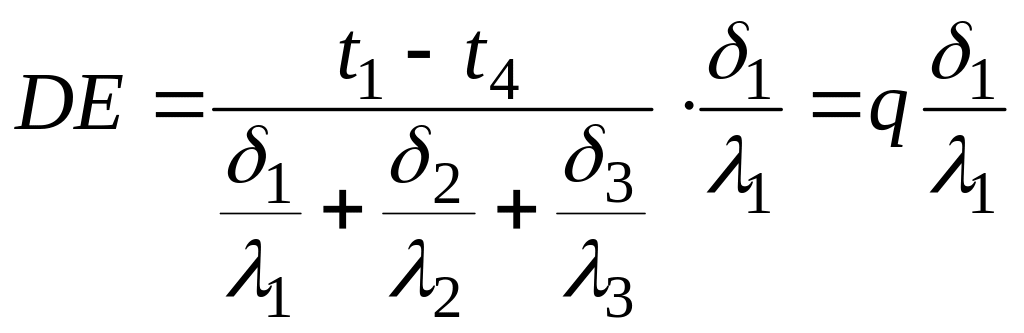
или в соответствии с одним из уравнений (21)

Аналогичным образом доказывается, что

Иногда ради сокращения выкладок многослойную стенку рассчитывают как однослойную (однородную) стенку толщиной Δ. При этом в расчет вводится так называемый эквивалентный коэффициент теплопроводности, значение которого определяется из следующего соотношения:

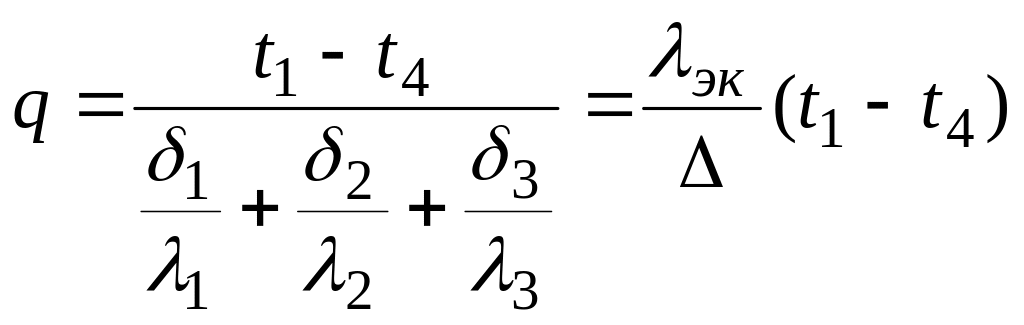(22)

Отсюда имеем, что

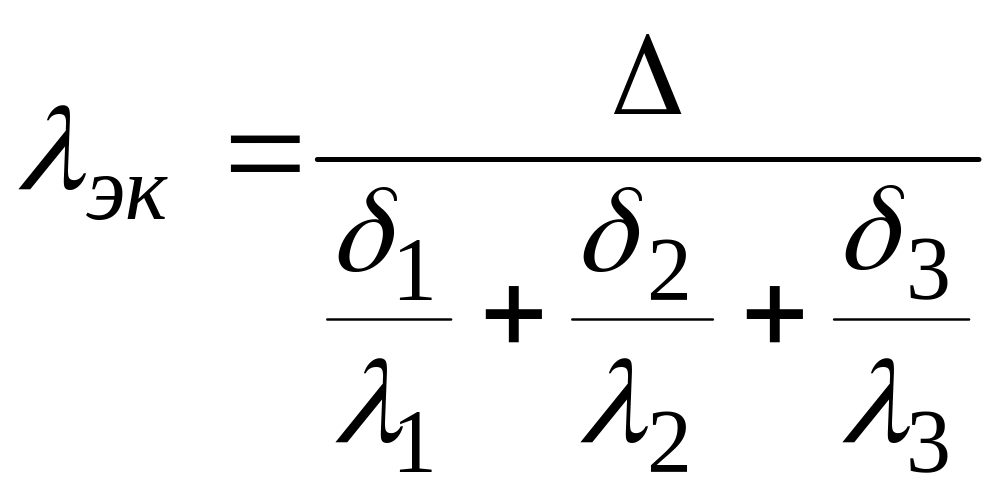(23)

Для п-слойной стенки получаем следующую формулу:

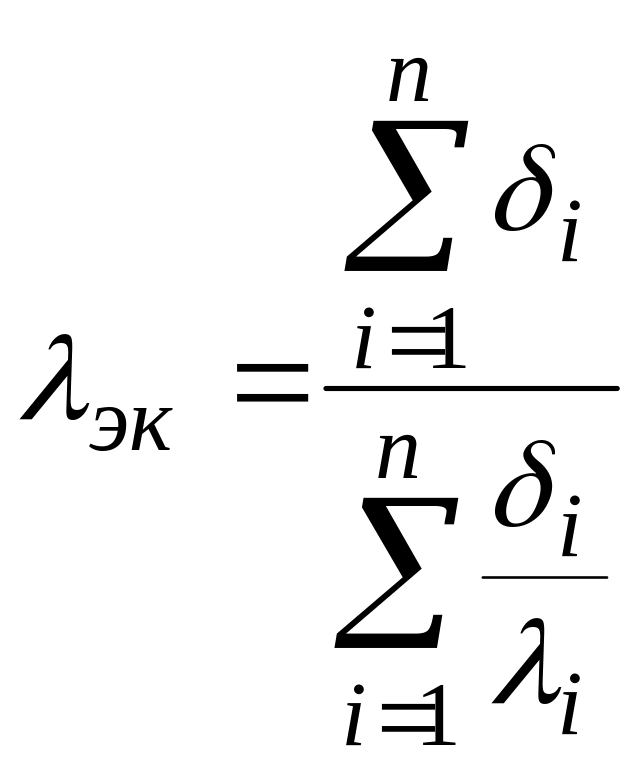(24)

Таким образом, эквивалентный коэффициент теплопроводности зависит только от значений термических сопротивле- ний и толщины отдельных слоев.

При выводе формулы для многослойной стенки мы пред-

полагали, что слои плотно прилегают друг к другу и благодаря хорошему контакту соприкасающиеся поверхности разных слоев имеют одну и ту же температуру. Однако, если повер-хности шероховаты, то тесное соприкосновение невозможно и между слоями образуются тонкие воздушные зазоры. Так как теплопроводность воздуха мала (λ = 0,02), то наличие даже очень тонких зазоров может сильно сказаться в сторону уменьшения эквивалентного коэффициента теплопроводности многослойной стенки. Аналогичное влияние оказывает и слой окисла металла. Поэтому при расчете, и в особенности при измерении теплопроводности многослойной стенки, на плотность контакта между слоями нужно обращать особое внимание.

Пример 1-1. Определить часовую потерю тепла через кирпичную стенку длиной 5 м, высотой 3 м и толщиной 250 мм, если на поверхностях поддерживаются температуры t₁ = 20°С и

t₂ = - 30^оС. Коэффициент теплопроводности кирпича

λ = 0,6 Вт/м К.

Согласно уравнениям (1.4) и (1.5)

Вт/м²

Вт

Пример 1-2. Каково значение коэффициента теплопроводности материала стенки, если при δ = 300 мм и Δt = 1000° С , q = 900 Вт/м²

Согласно формуле (1.4) имеем:

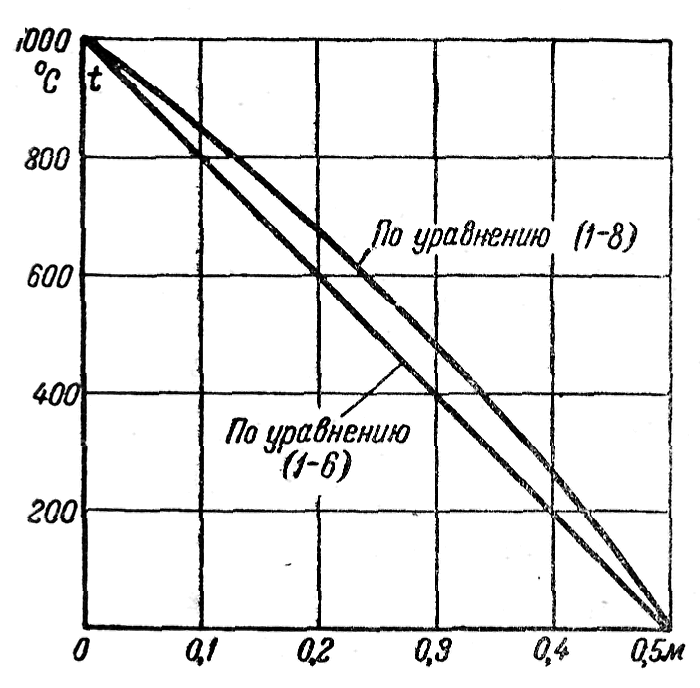
Пример 1-3. Определить тепловой поток q через плоскую шамотную стенку толщиной δ = 0,5 м и найти действительное распределение температуры, если t₁=1 000° С, t₂ = 0° С и λ = 1,0 (1+ 0,001 t ) Вт/м К

Сначала вычислим среднюю температуру стенки t_ст

^оС

По этой средней температуре t_т определим среднее значение коэффициента теплопроводности λ_т:

λ _ст = 1,0(1 +0,001 t _ст ) = 1,5 Вт/м К.

Подставляя полученное значение λ _ст в уравнение (12), получим:

, Вт/м²

Точно такой же результат получим и при расчете по формуле (15). Действительное распределение температуры в стенке определяется по уравнению (17). Результаты подсчетов приведены в таблице 2 и на рисунке 3. Для сравнения приведены результаты расчета по формуле (13).

Таблица 2 Распределение температур в стенке

х, м	0	0,1	0,2	0,3	0,4	0,5	Примечание
tх' °С tх' °С	1000 1000	845 800	675 600	480 400	265 200	0 0	формула(1.8) формула(1.6)

Рис. 9. Распределение температур в стенке при переменном и постоян­ном коэффициентах теплопровод­ности