Стационарная теплопроводность плоской стенки
Основываясь на законе Фурье, можно вывести расчетные формулы теплопроводности.
Однородная стенка
Рассмотрим однородную стенку толщиной δ (рис.6). Коэффициент теплопроводности материала постоянен и равен λ. На наружных поверхностях стенки поддерживаются постоянные температуры t1 и t2. Температура изменяется только в направлении оси х, перпендикулярной плоскости стенки. Следовательно, в этом случае температурное поле одномерно, а плоские изотермические поверхности располагаются перпендикулярно оси х.
Выделим внутри стенки на расстоянии х от поверхности слой толщиной dх, ограниченный двумя изотермическими поверхностями. На основании закона Фурье (уравнение 6 ) для этого слоя можно написать плотность теплового потока
Рис. 6 Однородная плоская
стенк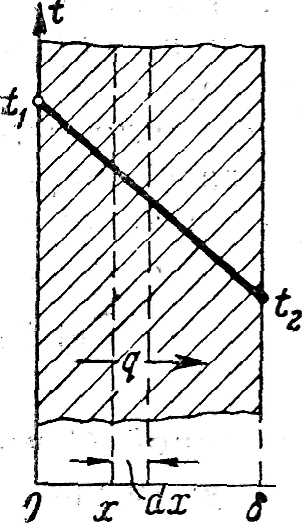а
(11а)
Разделив переменные, получаем:
(11в)
Интегрирование последнего уравнения дает:
(11с)
Постоянная интегрирования С определяется из граничных условий, а именно: при х =0 t = t1. Подставляя это значение в уравнение (11с), получаем:
С = t1 (11д)
При х =0 t = t2 , следовательно,
(11е)
Последнее уравнение позволяет определить неизвестную величину плотности теплового потока q, а именно:
(12)
Следовательно, количество тепла, переданное через 1 м2 стенки в единицу времени с, прямо пропорционально коэффи-циенту теплопроводности λ и разности температур наружных поверхностей стенки Δt и обратно пропорционально толщине стенки δ. При этом следует особо отметить, что тепловой поток определяется не абсолютным значением температур, а их разностью - температурным напором Δt = t 1 - t2. Уравнение (12) является расчетной формулой теплопроводности плоской стенки. Она связывает между собой четыре величины: q, λ, δ и Δt.
Зная
из них любые три, можно найти четвертую.
Отношение
Вт/м2
К
называется тепловой
проводимостью стенки, а
обратная величина
м2
К/ Вт
- тепловым
или
термическим
сопротивлением стенки. Последнее
определяет падение температуры при
прохождении через стенку удельного
теплового потока, равного единице.
Определив по формуле (12) величину
плотности теплового потока, легко
вычислить и общее количество тепла Q,
переданное через плоскую стенку
поверхностью F (м2)
в
течение времени τ
(12а)
Если в уравнение (11с) подставим значение постоянной С из уравнения (11д) и значение q из уравнения (12), то получим уравнение температуры по толщине стенки распределения
(13)
Последнее является уравнением прямой линии. Следовательно, при постоянном значении коэффициента теплопроводности температура однородной стенки изменяется по закону прямой.
Дополнительные сведения. В действительности же вследствие зависимости от температуры коэффициент теплопроводности является переменной величиной. Если это обстоятельство учесть, то получим иные, более сложные расчетные формулы. Для подавляющего большинства материалов зависимость коэффициента теплопроводности от температуры получается линейной, например λ = λ 0(1 + bt ). В этом случае на основании закона Фурье для плоской стенки имеем:
(14а)
Разделив переменные и произведя интегрирование, получим
(14в)
в уравнение (14в) граничные значения переменных, имеем
при
х
= 0 t
=
t1
и
и
;
(14с)
при
х
= δ t
=
t2
и
и
;
(14д)
Вычитая из второго равенства (14с) первое (14д), находим:
,
(14е)
Откуда
(15)
Это и есть новая расчетная формула, которая по сравнению с формулой (12) несколько сложнее. В формуле (12) мы принимаем коэффициент теплопроводности постоянным и равным некоторому среднему значению λт. Теперь, приравнивая, правые части формул (12) и (15), имеем:
(16 )
Следовательно, если λт определяется по формуле (6), т. е. по
среднеарифметическому из граничных значений температуры стенки, то формулы (12) и (15) равнозначны.
Уравнения температурной кривой в стенке получается путем решения квадратного уравнения (14в) относительно t и подставляя значения С из уравнения (14с), а именно:
(17)
Из этого уравнения следует, что в действительности температура стенки изменяется не по прямой, а по кривой. В некоторых случаях изменение температуры в стенке требуется рассчитывать по этой более сложной формуле (17).