3.8.2 Уравнение переноса лучистой энергии

При прохождении тепловых лучей в поглощающей газовой среде поглощенная лучистая энергия переходит в теплоту и излучается этой средой. В результате процессов поглощения и переизлучения происходит перенос лучистой энергии и тепла в поглощающей среде.

Пусть имеется слой газа, на который падает поток лучистой энергии, имеющий сплошной спектр. Некоторая часть лучей при этом пройдет через поглощающую среду без изменения интенсивности, и только лучи, имеющие определенную длину, будут поглощаться газом. Интенсивность потока лучистой энергии по мере прохождения через слой газа будет постепенно уменьшаться (рис. 39).

Рис. 39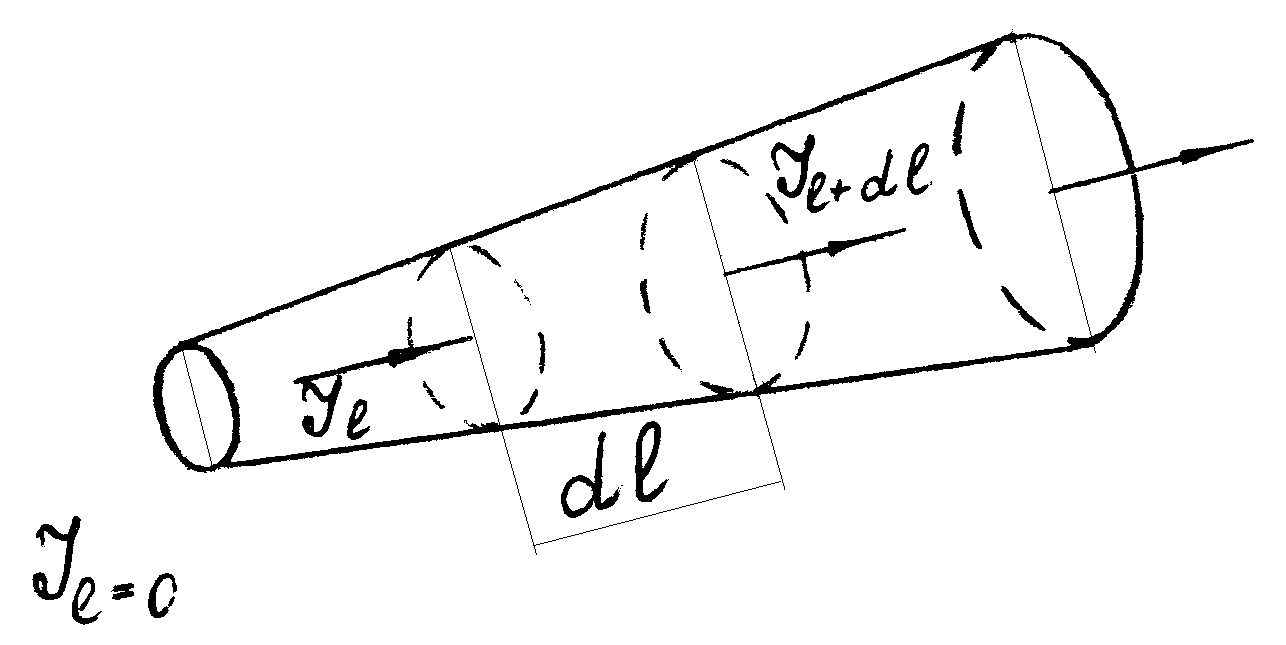

Приближенно принимается, что ослабление интенсивности излучения по отдельным длинам волн при прохождении через слой поглощающего газа толщиной dℓ уменьшается пропорционально этой интенсивности и бесконечно малому прохождению пути луча dℓ

. (169)

Здесь k_λ – коэффициент поглощения или правильнее коэффициент ослабления луча.

Это выражение является основным законом переноса лучистой энергии в поглощающей среде – законом Бугера. Его можно представить в виде:

. (170)

Полагая, что при ℓ = 0 i_l = i_lо = 0, после интегрирования последнего уравнения получим:

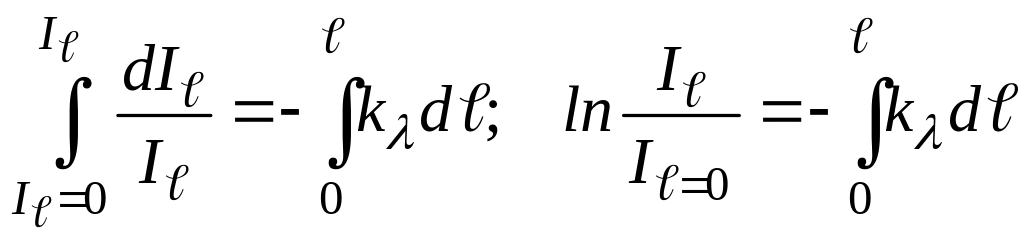(171)

откуда

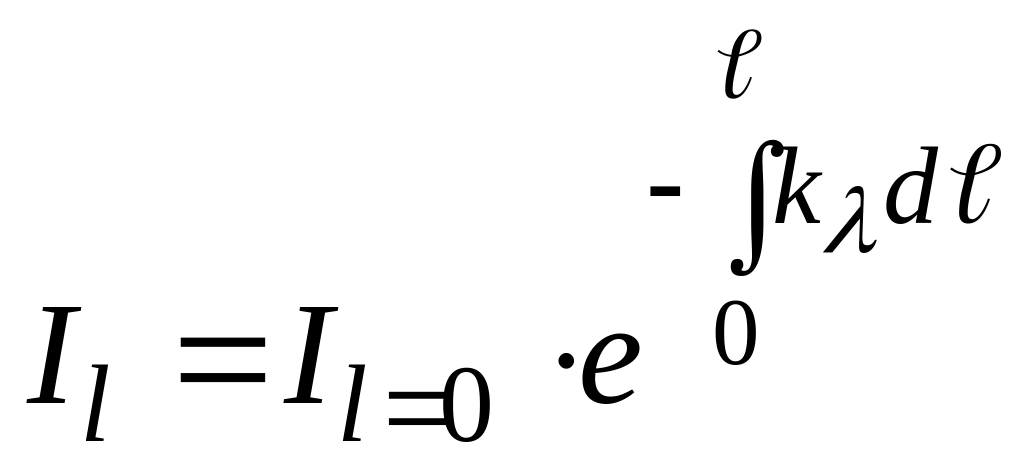. (172)

Согласно закону Стефана-Больцмана излучательная способность для отдельных полос излучения среды представится зависимостью:

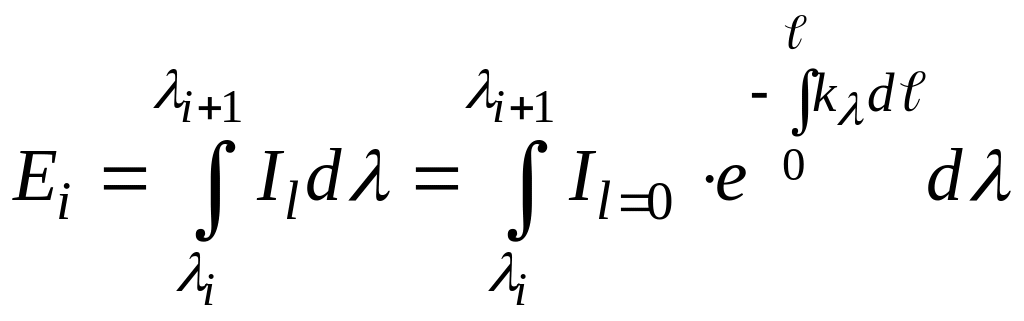. (173)

Интенсивность излучения i_lо находится по закону Планка. Поглощательная способность определяется по отношению лучистой энергии, поглощенной средой в слое толщиной ℓ, к энергии излучения, падающей на этот слой i_l=0

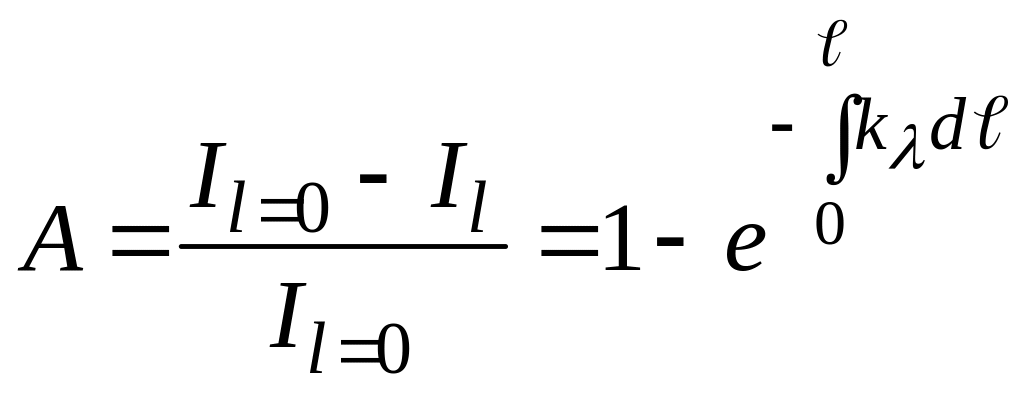. (174)

При прохождении теплового луча через слой из смеси газов, эффект поглощения будет тем больше, чем больше парциальное давление поглощающего газа. В соответствие с законом Бэра коэффициент ослабления равен:

, (175)

где b_λ – температурный коэффициент;

Р_i – парциальное давление газа.

Таким образом, выражение для спектральной поглощательной способности плоского слоя газа, в соответствие с законами Бугера и Бэра принимает вид:

. (176)

Если считать, что интегральная степень черноты газа ε_г определяется выражением

,

где Е_г – собственное излучение газа,

то формула для определения ε_г будет иметь вид

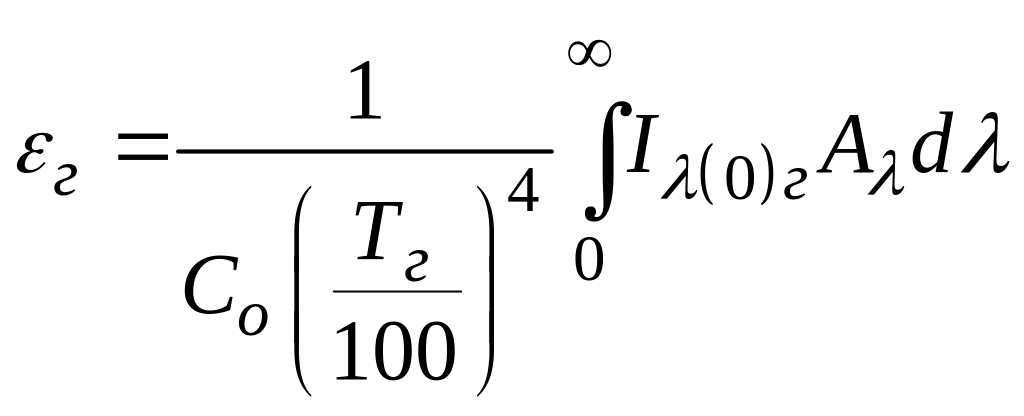. (177)

Интегральная поглощательная способность газа будет иметь вид

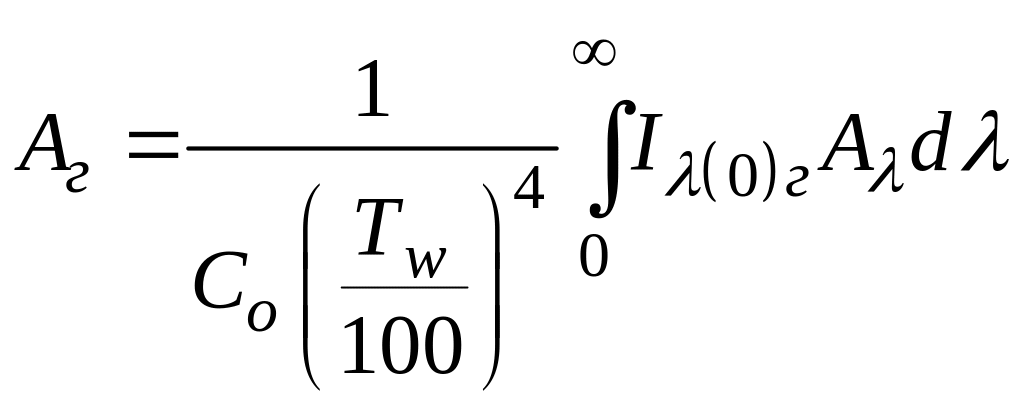. (178)

Несмотря на очевидное различие степени черноты газа и его поглощательной способности в инженерных расчетах обычно полагают эти величины одинаковыми.

Таким образом, для определения поглощательной и излучательной энергии среды необходимо располагать данными по спектрам поглощения и излучения, а также по коэффициентам ослабления для всех полос спектра.

Коэффициент ослабления луча в общем случае не является постоянной величиной. Он зависит от природы излучающей среды, длины волны и температуры. Вследствие этого коэффициенты оказываются весьма различными не только для отдельных полос спектра, но существенно изменяются в пределах одной и той же полосы.

Приведенные уравнения лучистой энергии относятся к поглощательной среде, переизлучения которой незначительно, распределение температуры по объему газа является равномерным.