3.4 Лучистый теплообмен между двумя серыми телами

3.4.1 Две небольшие и далекие поверхности

Пусть имеются две небольшие плоские серые поверхности dF₁ и dF₂ (рис. 33). Расстояние между их центрами r; одна из поверхностей имеет температуру Т₁ и коэффициент излучения .

Рис. 33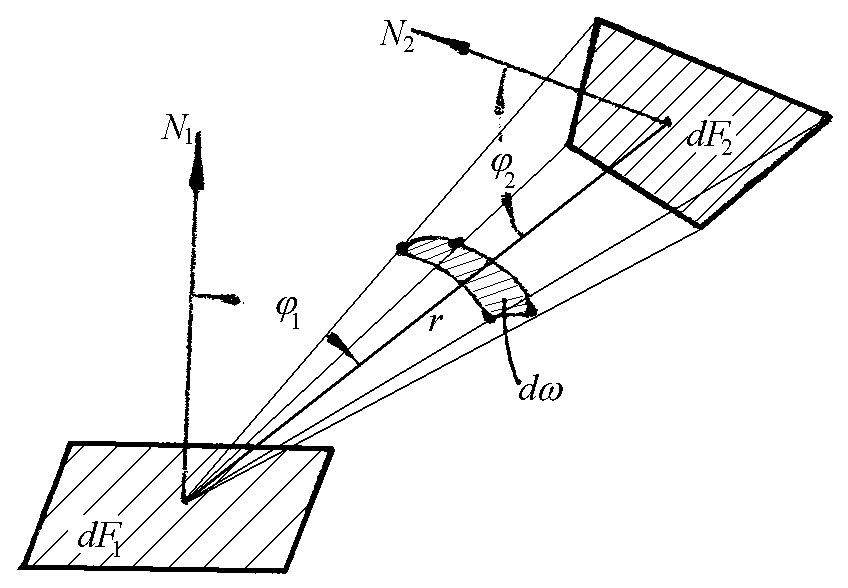

Нормаль N₁, восстановленная в ее центре, образует угол φ₁ с линией, соединяющей центры обеих поверхностей. Для второй поверхности соответственно известны Т₂, и φ₂. Причем Т₂ < Т₁. Поверхности dF₁ и dF₂ могут быть расположены в пространстве произвольно, если только с одной поверхности можно «видеть» другую.

Обозначим через dω пространственный угол, под которым поверхность dF₂ видна из центра поверхности dF₁. Этот пространственный угол определяется выражением

. (129)

Так как излучающая поверхность dF₁ и пространственный угол dω малы, то лучистый поток, падающий с dF₁ на dF₂ будет являться величиной второго порядка малости и его можно обозначить через . Численно этот поток, согласно формулам (117) и (127), равен

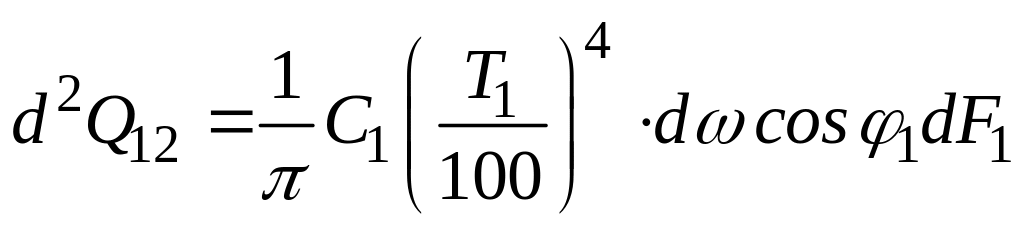, Вт (130)

или

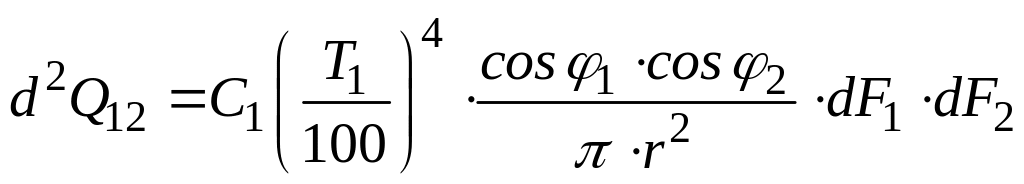, Вт. (131)

Так как поверхность dF₂ не является абсолютно черной, то она будет поглощать не весь теплового поток, а только его часть:

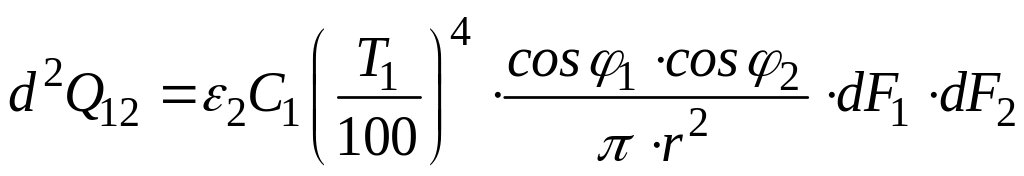, Вт. (132)

Аналогично можно написать выражение, которое определяет величину теплового потока, излучаемого поверхностью dF₂ и поглощается поверхностью dF₁

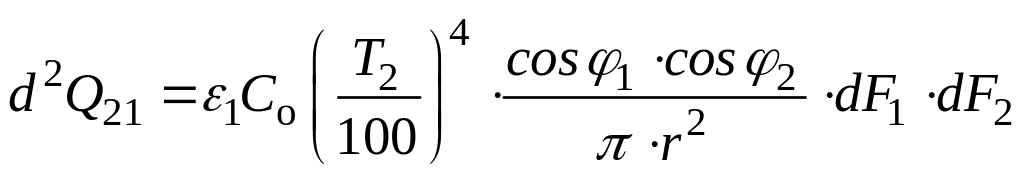, Вт.

Если Т₁ > Т₂, то тепловой результирующий поток, передаваемый излучением с поверхности dF₁ поверхность dF₂, и пошедший на нагрев будет равен разности и , т.е.

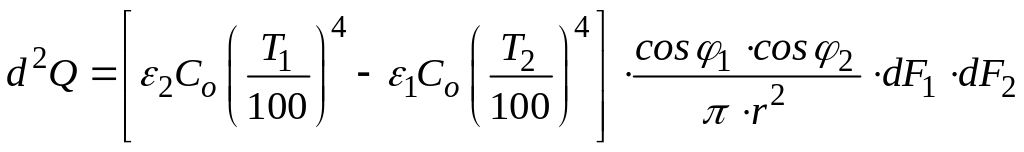. (133)

Так как , то .

В результате получаем окончательную формулу

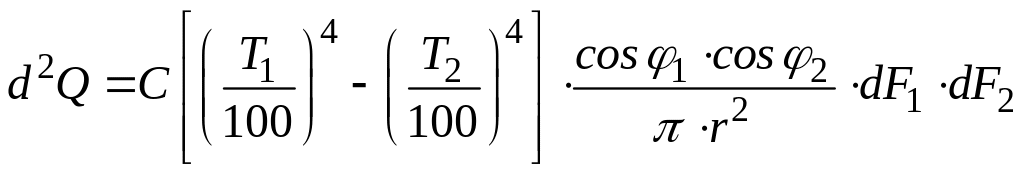, (134)

где - приведенный коэффициент излучения.

При выводе формулы (134) не учитывался лучистый теплообмен поверхностей dF₁ и dF₂ с окружающим пространством.

3.4.2 Лучистый теплообмен между двумя телами,

произвольно расположенными в пространстве

Если мы возьмем две поверхности конечных размеров, расположенных произвольно в пространстве, но «видящих» друг друга, то предыдущие рассуждения справедливы для элементов поверхностей dF₁ и dF₂.

Для того чтобы определить результирующий тепловой поток лучистой энергии между поверхностями F₁и F₂ необходимо проинтегрировать это выражение по поверхностям F₁и F₂ и получим:

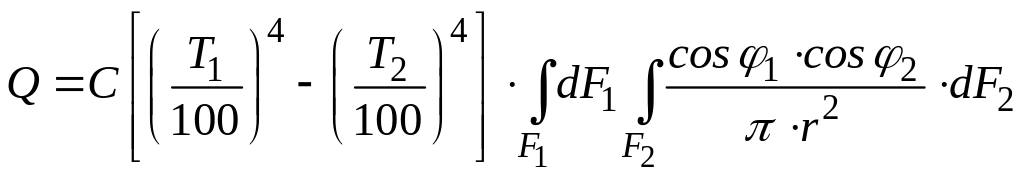(135)

или окончательно

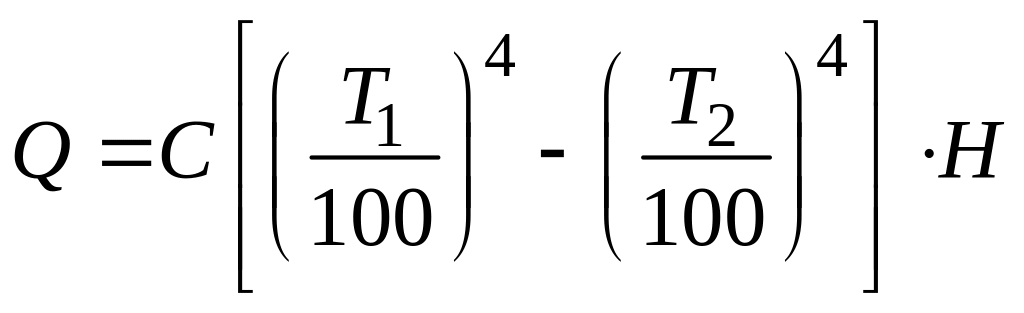(136)

где 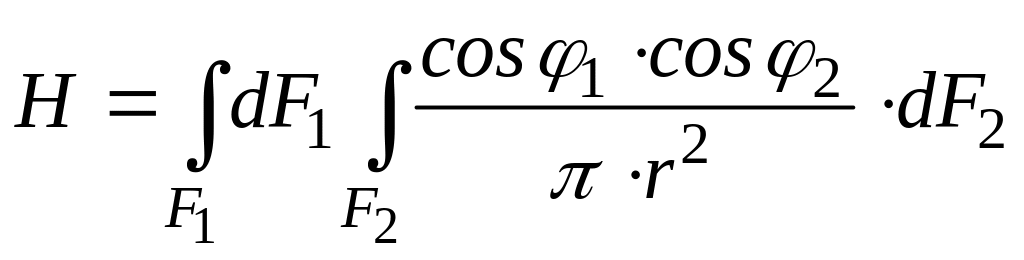- взаимная излучающая поверхность тел 1 и 2.

Величину Н можно определить по формуле

, (137)

где

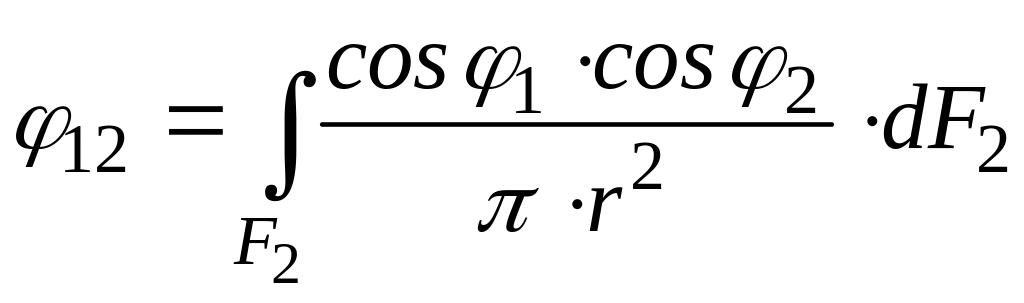. (138)

Входящие в эту формулу φ₁₂ и φ₂₁ называются угловыми коэффициентами. Они не зависят от температур, коэффициентов лучеиспускания, абсолютного значения размеров обеих поверхностей, разделяющего их расстояния. Они определяются исключительно углами, характеризующими взаимное расположение обеих поверхностей в пространстве.

В общем виде угловой коэффициент с поверхности F₁ на поверхность F₂ может быть найден путем двойного интегрирования

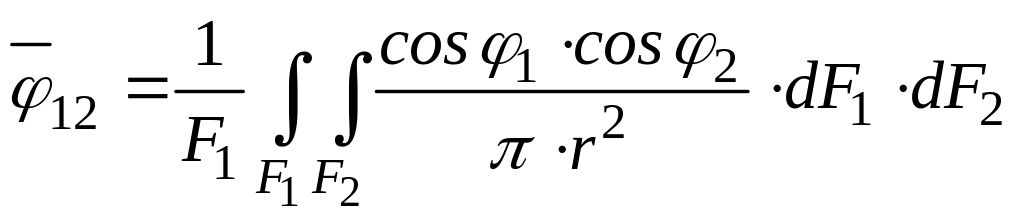. (139)

Обратный угловой коэффициент с поверхности F₂ на поверхность F₁ определяется аналогично:

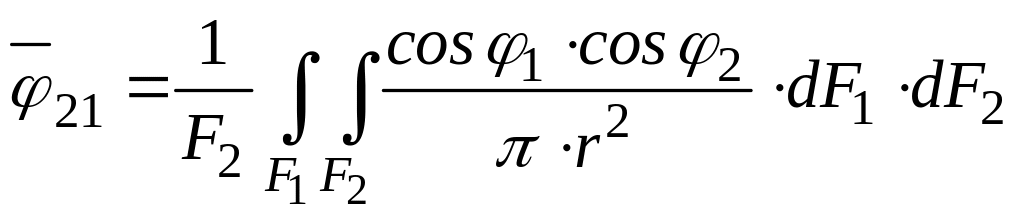. (140)

Для любой пары поверхностей двойной интеграл имеет одно и тоже числовое значение. Поэтому во всех случаях справедливо равенство

. (141)

Полученное выражение называется принцип взаимности. Если например, известен один из угловых коэффициентов излучения, то другой определяется из зависимости:

. (142)

В общем случае может иметь место теплообмен излучением между п телами. Если учесть лучистый теплообмен данного тела со всеми окружающими его телами, то можно получить зависимость, выражающую свойство замыкаемости потоков тепла. Для результирующих потоков излучения какого-либо тела имеет место соотношение:

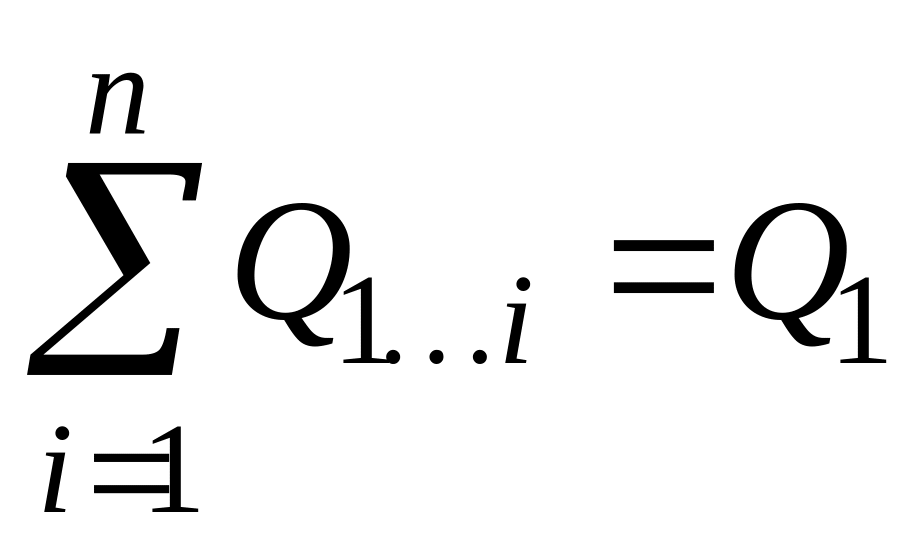. (143)

Так как

, (144)

то

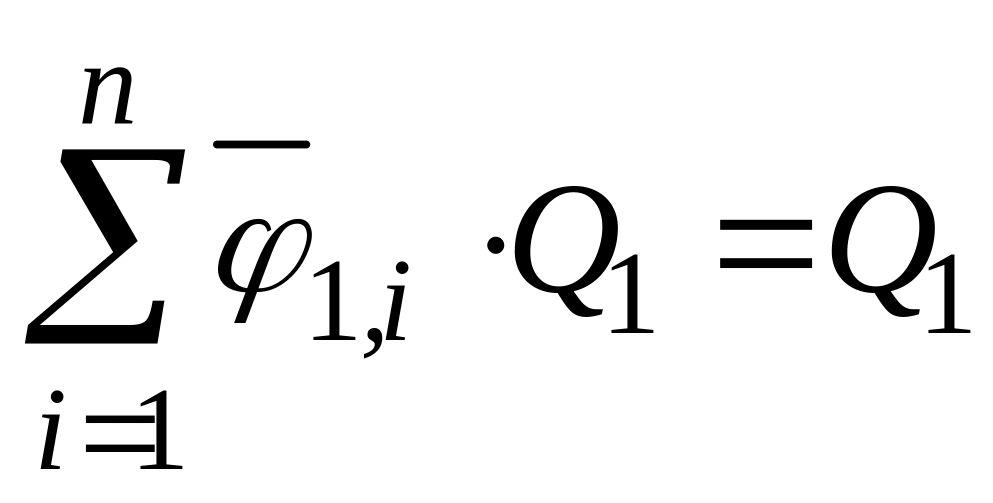, (145)

Откуда

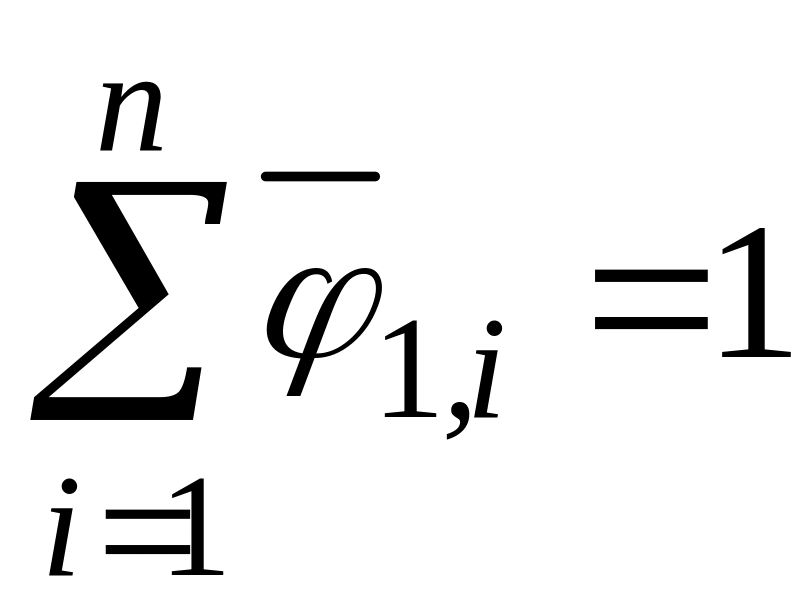. (146)

Согласно уравнений (145) и (146) взаимные поверхности излучения

. (147)

Следовательно,

. (148)

Зависимости (143), (146) и (148) выражают свойство замыкаемости лучистого теплообмена рассматриваемого с окружающими его телами. При этом принимается, что может иметь место самооблучение тела ( ), т.е. в общем случае часть энергии излучения данного тела может попасть на то же тело.

Свойство затемнимости состоит в том, что результирующий поток от тела 1 к телу 2 равен нулю, если на пути лучей находится непрозрачное тело. Тогда . Для плоского и выпуклого тел самооблучение отсутствует и, следовательно, . Для вогнутых тел . Как следует из изложенного, в общем случае угловые коэффициенты могут изменяться от нуля до единицы.

Наиболее просто угловые коэффициенты могут быть вычислены для замкнутых систем, которые состоят из двух поверхностей такой формы, что угловые коэффициенты с любого элемента поверхности 1 на поверхность 2 сохраняют постоянное числовое значение. И, в свою очередь, угловой коэффициент с любого элемента поверхности 2 на поверхность 1 имеет тоже постоянное числовое значение

.

Рис. 34 а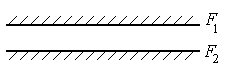

Система двух тел, удовлетворяющих этому условию изображена на рисунке

а) две большие плоские поверхности, расположенные на небольшом расстоянии одна от другой.

б) две концентрические сферические поверхности или два круглых коаксиальных бесконечно длинных цилиндра (тело 1 внутри тела 2).

.

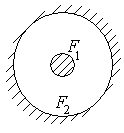
Рис. 34 б

в) внутренняя поверхность шарового сегмента и плоская круглая поверхность, являющаяся основанием сегмента (F₁ - плоская поверхность, F₂ – вогнутая).

.

Рис. 34 в

г) две поверхности, составляющие сферическую полость, контуры их могут быть произвольной формы

.

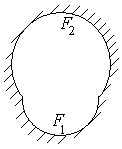
Рис. 34 г

При выполнении приближенных технических расчеты эти простые формулы для определения φ₁₂ и φ₂₁ часто применяют и для таких замкнутых систем из двух тел, для которых условие (21) не соблюдается.