3.3 Законы теплового излучения для условия равновесной среды

В силу общей природы электромагнитных волн основные законы, которым подчиняется излучение, являются для них общими. Эти законы получены применительно к идеальному телу, которым является абсолютно черное тело, и равновесному излучению.

Равновесным называется излучение, при котором все тела, входящие в данную излучающую систему, имеют одинаковую температуру.

Закон Планка является одним из основных законов излучения. Он устанавливает зависимость интенсивности излучения от температуры и длины волны

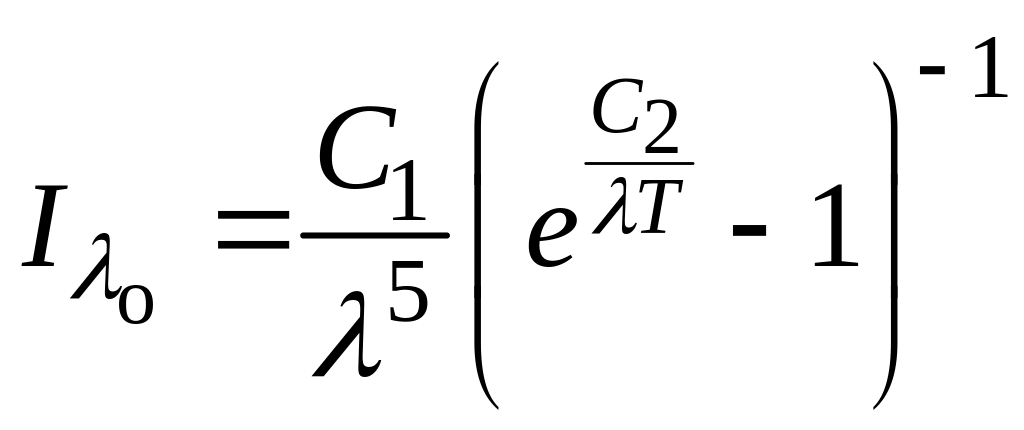, Вт/м³, (114)

где С₁ = 0,374^.10^-15 Вт·м² – первая постоянная Планка;

С₂ = 1,4388^.10^-2 м·К – вторая постоянная Планка;

 - длина волны, м;

Т – абсолютная температура, К.

Согласно уравнению (111) каждой длине волны соответствует свое значение интенсивности излучения. Распределение спектральной интенсивности излучения по длинам волн и температурам по закону Планка показано на рис. 29. Из рисунка следует, что интенсивность излучения, характеризующаяся отдельными изотермами, проходит через максимум. При длинах волн  = 0 и  = ∞ эта интенсивность обращается в нуль. С повышением температуры интенсивность излучения значительно увеличивается.

Рис. 29 – Зависимость спектральной интенсивности излучения абсолютно черного тела от длины волны и температуры

Поскольку закон Планка получен для идеального тела, то для реальных тел он выражает максимально возможную интенсивность излучения. Закон Планка подтверждается опытом.

Закон Вина устанавливает связь между температурой Т и длиной волны _тах, на которую падает максимум интенсивности излучения.

Положение максимумов в интенсивности излучения можно получить из экстремального значения функции. Для этого находится производная функции по длине волны. Приравнивая производную нулю, получим следующее трансцендентное уравнение:

.

Решение этого уравнения дает:

.

Отсюда

м·К или м, (115)

где _тах – длина волны, которой соответствует максимальная интенсивность.

Закон Стефана-Больцмана устанавливает зависимость плотности интегрального полусферического излучения от температуры. Плотность интегрального полусферического излучения определяется как суммарная энергия излучения тела по всем длинам волн:

.

После выполнения операции интегрирования получаем зависимость:

, Вт/м². (116)

Величина σ_о = 5,67·10^-8 Вт/м²·К⁴ весьма мала, а величина Т⁴ обычно очень велика.

Для удобства практических расчетов последняя зависимость обычно представляется в форме

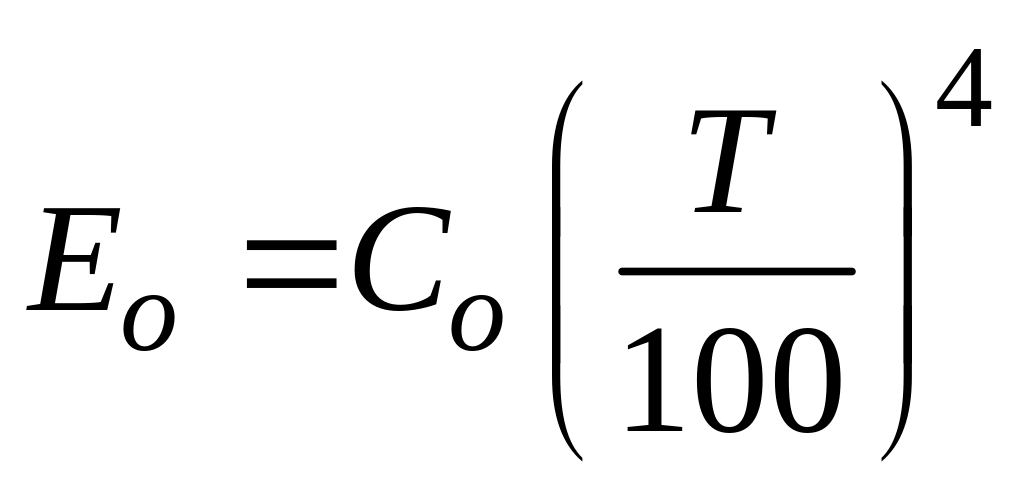, Вт/м², (117)

где 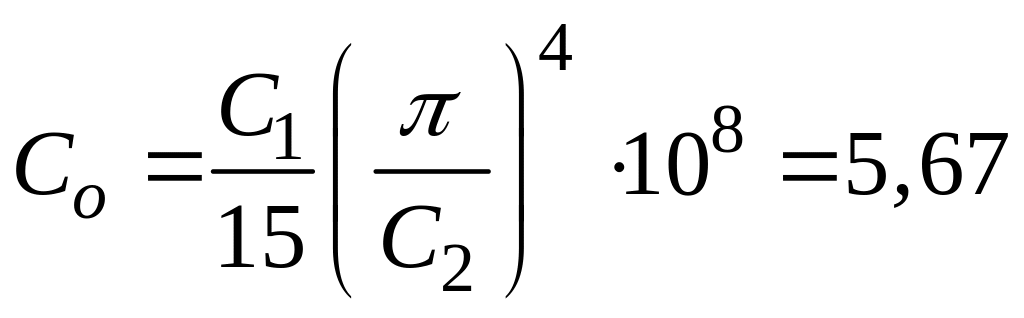Вт/м²·К⁴ - коэффициент излучения абсолютно черного тела.

Согласно закону Стефана-Больцмана плотность полусферического интегрального излучения зависит только от температуры и изменяется пропорционально четвертой степени абсолютной температуры.

Закон Стефана-Больцмана может быть применен к серым телам. Если спектральная интенсивность излучения диффузно излучающего тела для всех длин волн составляет одну и ту же долю ε от спектральной интенсивности излучения абсолютно черного тела при той же температуре, то такое тело называется серым. В этом случае используется положение о том, что у серых тел так же как и черных, собственное излучение пропорционально абсолютной температуре в четвертой степени, но излучательная способность меньше, чем излучательная способность абсолютно черных тел при той же температуре. Тогда этот закон для серых тел принимает вид:

.

После интегрирования имеем:

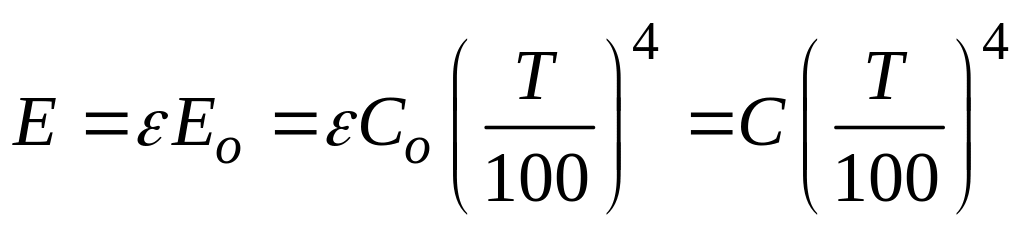. (118)

Здесь - интегральная или средняя степень черноты серого тела;

С – его коэффициент излучения, Вт/м²·К⁴.

Интегральная степень черноты может быть также представлена как отношение излучательной способности реального тела к излучательной способности абсолютно черного тела при той же температуре, что видно из уравнения (6.17):

. (119)

Рис. 30 – К выводу закона Кирхгофа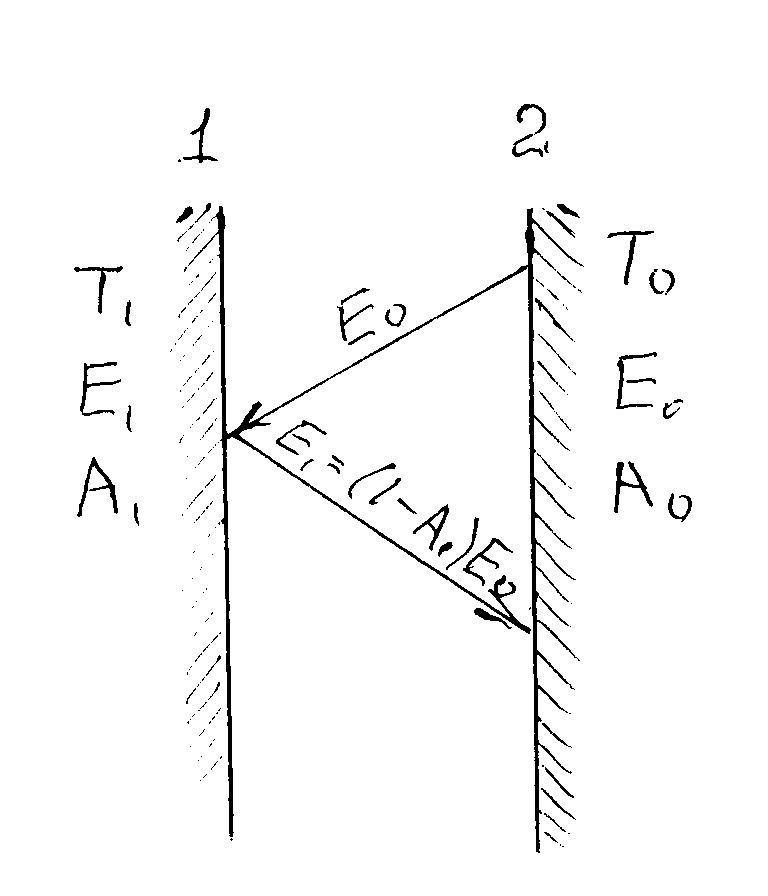

Закон Кирхгофа устанавливает связь между излучатальной и поглощательной способностями серых и абсолютно черных тел.

Пусть имеются две параллельно плоские поверхности 1 и 2 и расстояние между этими поверхностями настолько мало, что излучение с одной поверхности полностью попадает на другую (рис. 30). Выделим на каждой из поверхностей по участку площадью 1 м² так, чтобы эти участки быль расположены точно один против другого. Пусть поверхность 1 будет серая, а поверхность 2 абсолютно черная. Абсолютную температуру, излучательную способность и поглощательную способность этих поверхностей соответственно обозначим через Т₁, Е₁, А₁, Т_о, Е_о и А_о = 1.

Рассмотрим тепловой баланс процессов лучистого теплообмена для серой поверхности при условии неизменности температур. В этом случае, на основании второго начала термодинамики, должно существовать подвижное тепловое равновесие, т.е. приход (поглощение) тепла на каждой из поверхностей должен быть равен его расходу (излучению). С абсолютно черной поверхности 2 излучается и попадает на серую поверхность 1 тепловой поток

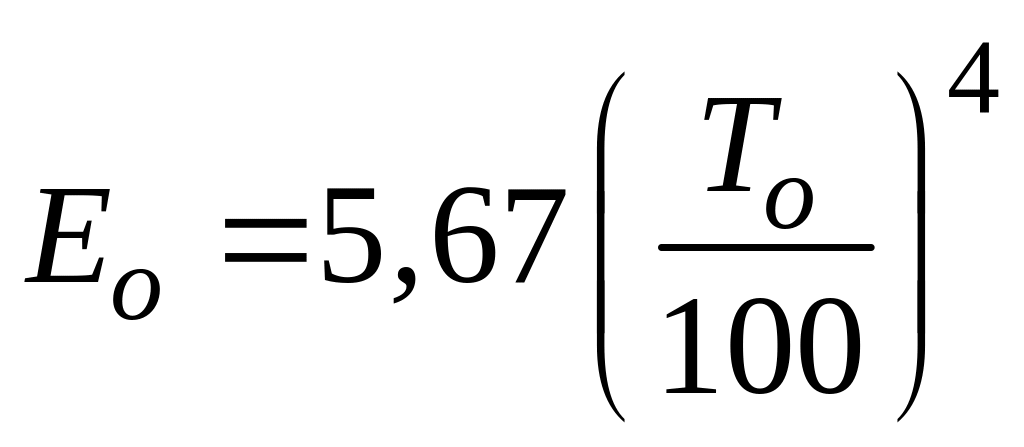, Вт/м². (120)

Из этого теплового потока поверхность 1 поглощает только А₁·Е_о Вт/м², а непоглощенная часть лучистого потока, которая равна (1-А₁)·Е_о Вт/м², отражается от поверхности 1, возвращается на поверхность 2 и поглощается ею. Сама поверхность 1 излучает, тепловой поток

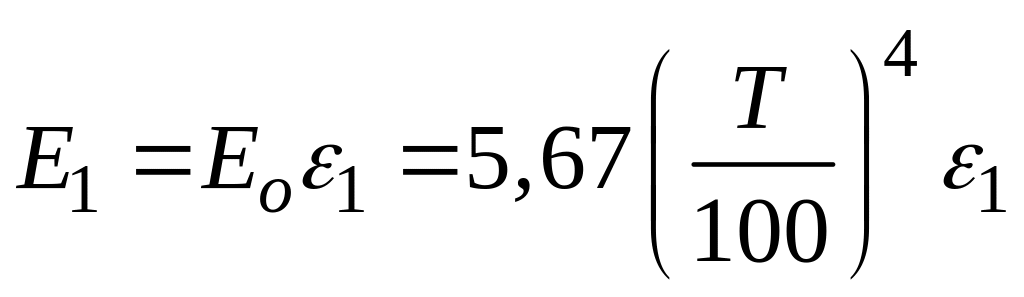, Вт/м², (121)

который попадает на поверхность 2 и целиком поглощается ею.

При равенстве температур обеих поверхностей Т₁ и Т_о тепловой поток, излучаемый серой поверхностью должен быть равен тепловому потоку, который она поглощает. Следовательно,

или

. (122)

Серая поверхность, характеризуемая поглощательной способностью А₁, может быть заменена любыми другими серыми поверхностями, у которых поглощательная способность А₂, А₃ и т.д. Поэтому полученную зависимость, называемую законом Кирхгофа, можно представить в более общем виде:

(123)

И сущность закона Кирхгофа может быть сформулирована следующим образом: Отношение лучеиспускательной способности тела к его коэффициенту поглощения одинаково для всех тел, имеющих одинаковую температуру, и равно лучеиспускательной способности абсолютно черного тела при той же температуре.

Численное значение коэффициента поглощения А для всех серых тел тождественно равно численному значению их степени черноты ε, т.к.

. (124)

В дальнейшем буквой ε будем обозначать и степень черноты и коэффициент поглощения, считая, что обе эти величины равнозначны и не зависят от температуры.

Закон косинусов или закон ламберта устанавливает связь между количеством излучаемой телом энергии и направлением излучения. Согласно этому закону количество энергии, излучаемое элементом поверхности dF₁, в направлении элемента поверхности dF₂ (рис. 31), пропорционально количеству энергии, излучаемому этим элементом поверхности в направлении нормали dQ_n, умноженному на величину пространственного угла dω и cosφ, где φ – угол, который образует направление излучения с нормалью к излучаемой поверхности

Рис. 31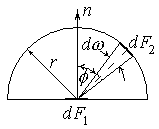

. (125)

Подставим в формулу (125) и получим

, (126)

где Е_п – плотность излучения площадки dF₁ в направлении нормали, Вт/м²,

Уравнение (126) показывает, что наибольшее количество энергии излучается площадкой в направлении нормали, т.е. при φ = 0. С увеличением угла φ количество излучаемой энергии уменьшается и при φ = 90^о становится равным нулю.

Так как плотность излучения Е_φ зависит от направления, то она может быть изображена в некотором масштабе в виде векторов, выходящих из центра излучающего элемента поверхности. Геометрическим местом концов всех векторов будет шаровая поверхность, радиус которой равен ½ Е_п.

Интегрируя количество энергии, излучаемой элементом поверхности по всем направлениям, можно установить, что лучеиспускательная способность в направлении нормали Е_п и лучеиспускательная способность по всем возможным направлениям Е_о связаны друг с другом соотношением

.

Следовательно, количество энергии, излучаемой элементом поверхности в пределах узкого конуса, ограничивающего пространственный угол dω с направлением нормали, будет равно

, Вт. (127)

Это выражение приходится интегрировать при определении так называемых угловых коэффициентов, необходимых при расчетах теплообмена излучением.

Закон квадратов расстояний. Представим себе поток лучистой энергии, излучаемый небольшим элементом какой-либо поверхности или точечным источником в пределах некоторого пространственного угла, который ограничен весьма узким конусом; вершина конуса лежит в центре источника излучения (рис. 32).

Рис. 32

Если среда совершенно прозрачна, то общая мощность лучистого потока будет оставаться постоянной на любых расстояниях от вершины конуса. Однако, плотность лучистого потока (Вт/м²), т.е. его мощность, отнесенная к единице площади поперечного сечения потока, не может оставаться постоянной вследствие того, что поперечное сечение лучистого потока возрастает по мере увеличения расстояния от вершины конуса. Так как радиус основания конуса возрастает прямо пропорционально расстоянию этого основания от вершины конуса, а площадь основания пропорциональна квадрату его радиуса, то плотность лучистого потока изменяется обратно пропорционально квадрату расстояния от источника излучения. Эта зависимость называется законом квадратов расстояний и может быть выражена формулой

, (128)

где Е₁ – плотность лучистого потока на расстоянии 1 м от излучателя,

Е₂ – тоже, на расстоянии r.