2. 5 Моделирование процессов конвективного теплообмена

Теперь подробнее рассмотрим применение теории подобия к анализу процессов конвективного теплообмена.

Пусть имеются две подобные между собой системы.

Уравнение энергии, описывающее распределение температур внутри движущейся жидкости

Здесь - характеризует изменение температуры во времени.

Член характеризует изменение температуры при переходе от точки к точке, т.е. являет­ся конвективным изменением t.

Производные определяют интенсивность

изменения градиента температуры по направлению оси X. В таком случае подобные выражения могут служить мерой интенсивности из­менения потока тепла в направлении оси Х (т.к. ). Поэтому величина характеризует различие между тепловым потоком, подходящим к данной точке, и потоком, отходящим от нее. Именно этим различием и обусловлено изменение температу­ры в данной точке. То же самое можно сказать о направлениях по осям У и Z .

Следовательно, получаем пространственное распределение температуры вблизи точки поверхности. Уравнение теплоотдачи конвекцией на границе тел.

Вот этими двумя уравнениями и описываются условия , при кото­рых геометрически и механически подобные системы подобны и в тепловом отношении.

Итак, для первой системы будем иметь следующие уравнения теплопроводности и конвективного теплообмена

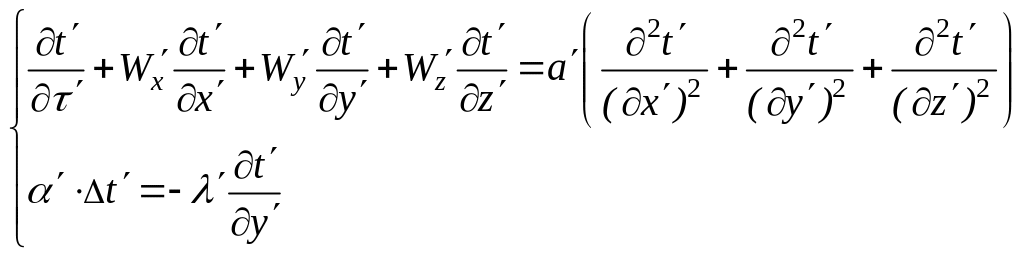(79)

и для второй системы соответственно:

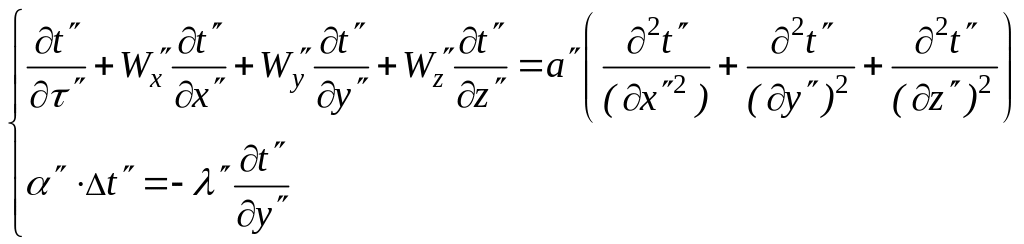(80)

на основании теории подобия имеем

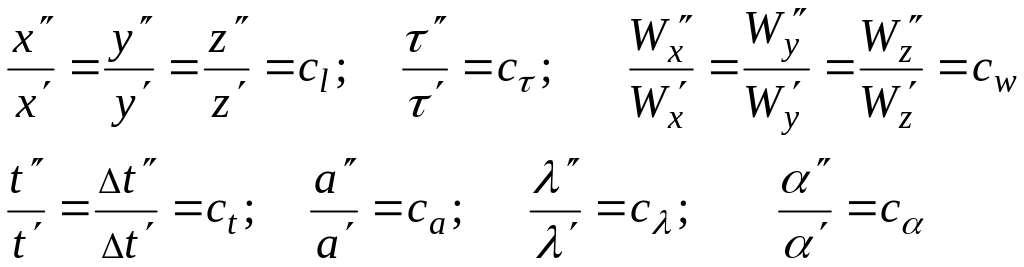(81)

Заменяя переменные второй системы через переменные первой получим систему II в виде

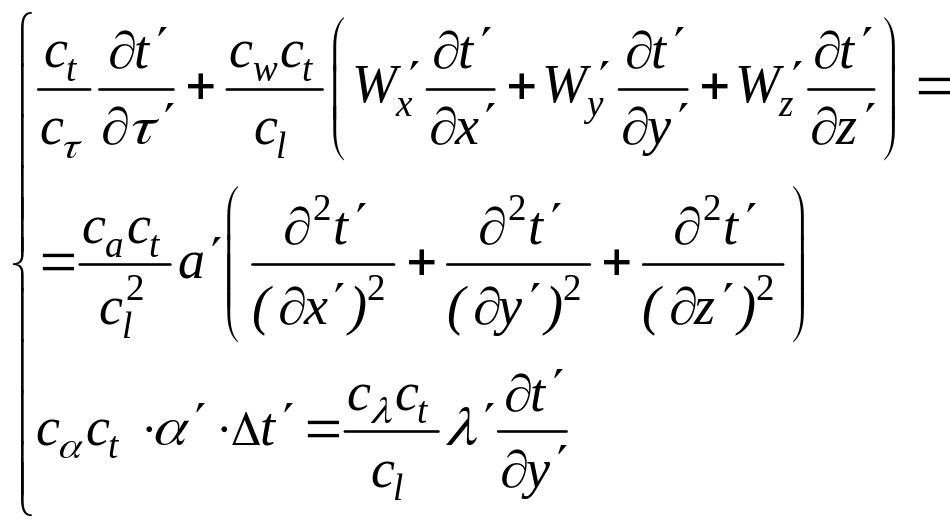(82)

Из обоих уравнений эти величины следует определять одним и тем же способом, Это возможно только при условии тождества уравнений, а для этого необходимо, чтобы комплексы, состав­ленные из констант подобия были одинаковые, а, следовательно, сократились. Отсюда возникают ог­раничительные условия

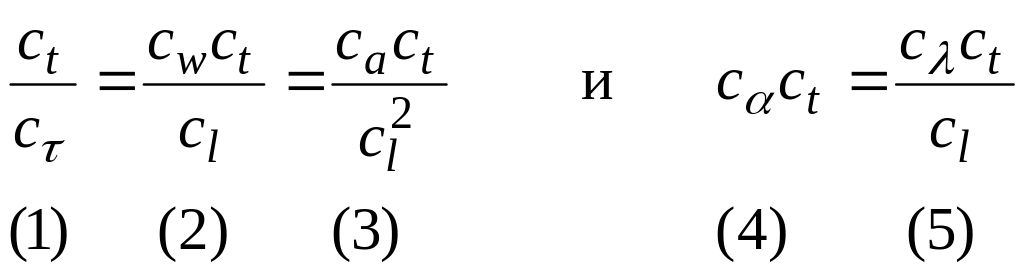(83)

Рассмотрим члены предыдущего равенства попарно и получим:

(84)

(85)

(86)

Подставляя теперь вместо констант подобия их значение из со­отношения (84,85,86) и произведя разделение переменных, по­лучим критерии теплового подобия

(критерий Фурье)

(критерий Пекле) (87)

(критерий Нуссельта)

Таким образом, при тепловом моделировании между собой двух или нескольких систем для любых сходственных точек критерии подобия Fо , Ре и Nu должны иметь одно и тоже значение. Критерий Рr можно преобразовать и представить в виде произведения двух критериев, а именно:

,

или же

Этот критерий получил название критерия Прандтля, который име­ет большое практическое значение в теплообмене. При экспериментальном изучении теплообмена конвекцией искомой величиной является коэффициент теплоотдачи α. Так как коэффициент теплоотдачи α входит в критерий Nu, то окончательное критериальное уравнение теплообмена имеет следующий вид:

Nu = f (Fо, Rе, Pr) (88)

В применении к отдельным задачам общее уравнение может быть упрощено, На основании второй теоремы подобия и для случая теплопередачи конвекцией может быть установлена соответству­ющая зависимость между определенными и определяющими крите­риями, Например, для стационарного вынужденного движения кри­териальное уравнение конвективного теплообмена принимает вид:

Nu = f ( Rе, Pr, . . . ) (89)

Для свободного движения:

Nu = φ ( Gr, Pr, . . . ) (90)

где l_о - основной размер системы, например, диаметр;

l - дл на трубы.

Критериальное уравнение конвекции составляют на основе тщательного анализа теплового процесса. Обычно зависимости между критериями подобия в этом случае представляются в виде степенных функций, например

(91)

где с, п, т, и к, - постоянные числа

Ввиду того что физические константы, входящие в выражение критериев Rе, Pr, и т.д. зависят от температуры, возникает необходимость учесть, так называемый температурный фактор Т_ст/ Т_w, в котором Т_ст - абсолютная температура обтекаемого твердого тела., а Т_w, - средняя температура, потока жидкости или газов.

В результате этого уточнения для конвективного теплообме­на можно принять, что

Nu = φ ( Rе, Pr, , ) (92)

В большинстве случаев температурные функции физических кон­стант можно приближенно апроксимировать линейной зависимостью и в результате перейти к формуле

Nu = φ ( Rе, Pr, , ) (93)

где μ_ст - коэффициент динамической вязкости потока при тем­пературе стенки;

μ_w - то же, но при температуре ядра потока.