2. 3. Дифференциальное уравнение теплопередачи конвекцией

Чтобы найти коэффициент теплоотдачи необходимо знать температурный градиент в формуле (69), а следовательно и распределение температур в жидкости. Последнее может быть получено из дифференциального уравнения теплопроводности, которое выводится на основе закона сохранения энергии.

Принято для каждого элементарного объема жидкости сумма изменений кинетической и внутренней энергий равна сумме подведенного тепла и выполненной работы.

Ограничимся более простой формулировкой этого закона, предположив, что изменение кинетической энергии и совершен­ной работы очень незначительно по сравнению с подведенным теплом.

В этом случае на основании допущения, что изменение внутренней энергии равно количеству подведенного тепла было получено дифференциальное уравнение передачи тепла конвекцией:

, (70)

где W_х, W_у, W_z – скорость движения в направлении осей х, у, z;

t – температура;

λ, с, ρ- соответственно коэффициент теплопроводности,

удельная теплоемкость и плотность жидкости.

Его называют дифференциальным уравнением теплопроводности в дви­жущейся жидкости или уравнением Фурье-Кирхгофа.

Поскольку в этом уравнении переменными величинами явля­ется не только температуры, но скорость и плотность, то при теоретических исследованиях теплопередачи конвекцией его сле­дует рассматривать совместно с уравнением сплошности и урав­нением движущейся вязкой несжимаемой жидкости, как единую систему уравнений, представляющую математическое выражение этого сложного теплового процесса в самом общем виде.

Уравнение (70) представляет собой полную производ­ную от температуры во времени. Такую производную, связанную с движущейся материей или субстанцией, называют субстанционной производной и обозначают одним символом:

(71)

Здесь - характеризует изменение температуры во времени в

какой-либо точке жидкости, т.е. является локальным

изменением t.

Член характеризует изменение температура при переходе от точки к точке, т.е. является конвективным изменением t .

Применим обозначение

Тогда, дифференциальное уравнение конвективного теплообмена (уравнение Фурье-Кирхгофа) можно записать в форме:

(72)

Если , то уравнение (5.18) переходит в уравнение теплопроводности. Уравнение конвективного тепло­обмена содержит пять неизвестных.

Чтобы сделать систему уравнений замкнутой, необходимо добавить уравнения, которые бы описывали изменение скорости во времени и пространстве. Такими уравнениями являются дифференциальные уравнения движения вязкой несжимаемой жидкости (уравнение Навье-Стокса),

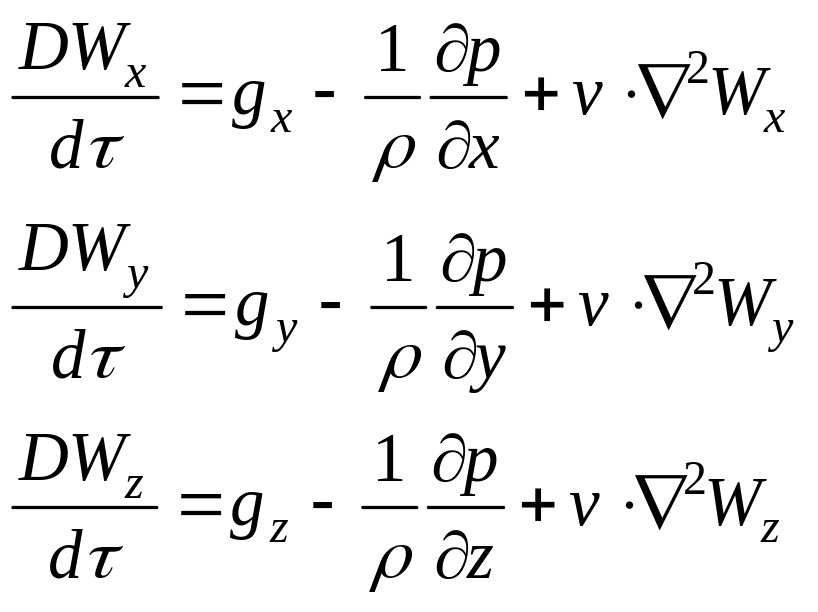(73)

где g_х, g_у, g_z – проекция ускорения силы тяжести;

Р – давление;

v – коэффициент кинематической вязкости, м²/с.

В векторной форме можно записи

(74)

Так как в уравнении движения, помимо W_х, W_y, W_z, вхо­дит еще одна неизвестная величина Р, то система уравнений не является замкнутой. Необходимо добавить еще одно уравнение и таким уравнением является дифференциальное уравнение сплош­ности (неразрывности).

Дифференциальное уравнение сплошности или наразрыв-ности для сжимаемых жидкостей

(75)

для несжимаемых жидкостей, полагая ρ = сопst , получим:

(76)

или то же самое

(77)

Таким образом, процесс конвективного теплообмена в несжима­емой однофазной среде описывается следующей системой диффе­ренциальных уравнений

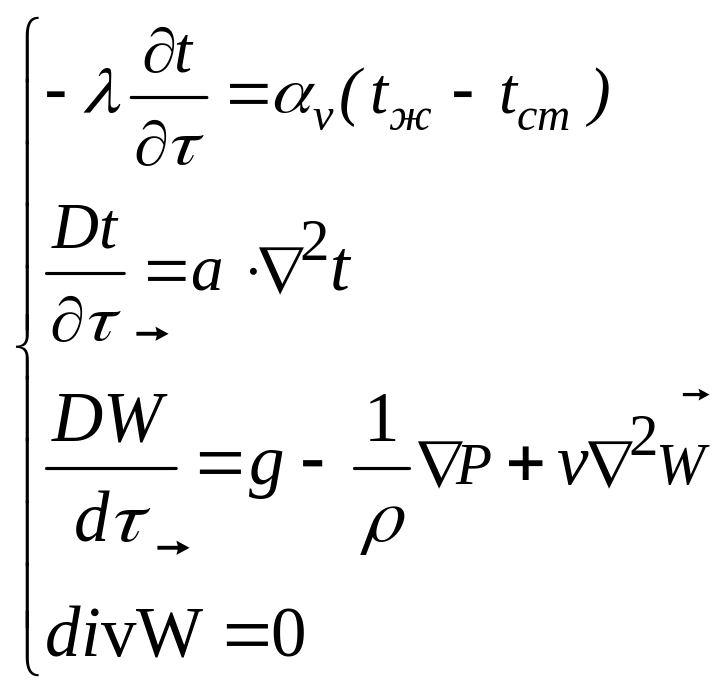(78)

Краевые условия. Так как дифференциальные уравнения выведены на основе общих законов физики, то они описывают явления в самом общем виде. Существует бесчисленное число процессов теплоотдачи, которые описываются указанными урав­нениями, но вместе с этим отличаются друг от друга некоторыми частностями. Чтобы ограничить задачу, из бесчисленного количе­ства выделить рассматриваемый процесс и определить его одно­значно, т. е. дать полное математическое описание, к системе дифференциальных уравнений необходимо присоединить матема­тическое описание всех частных особенностей, которые называют­ся условиями однозначности или краевыми условиями.

Условия однозначности состоят из:

1) геометрических условий, характеризующих форму и раз­меры тела, в котором протекает процесс;

2) физических условий, характеризующих физические свой­ства среды и тела;

3) граничных условий, характеризующих особенности проте­кания процесса на границах тела;

4) временных условий, характеризующих особенности проте­кания процесса во времени.

Условия однозначности могут быть заданы в виде числового значения, в виде функциональной зависимости или в виде диф­ференциального уравнения. Пусть, например, рассматривается случай теплоотдачи при движении жидкости в трубе. В этом слу­чае могут быть заданы такие условия однозначности:

1.Труба круглая, гладкая, диаметр трубы d и длина ее l.

2.Рабочим телом, т. е. теплоносителем, является вода, которая несжимаема, ее физические параметры равны: λ(t), с(t), μ(t) и γ(t). Если же зависимостью физических параметров от температуры можно пренебречь, тогда они задаются просто в виде числовых значений λ, с, μ и γ Если теплоносителем является сжимаемая жидкость (газы), то должно быть написано уравнение состояния этой жидкости.

3.Температура жидкости при входе равна t'_f, а на поверх­ности трубы - t_ω. Скорость при входе равна ω, а у самой стенки ω = 0. Если же температура и скорость при входе не постоянны, то должен быть задан закон их распределения по сечению.

4.Для стационарных процессов временные условия однознач­ности отпадают.

Итак, математическое описание процесса теплоотдачи состоит из: 1) уравнения теплообмена; 2) уравнения теплопроводности;

3) уравнения движения; 4) уравнения сплошности; 5) условий однозначности