1.6.3.3 Нагрев при передаче тепла конвекцией от среды с постоянной температурой

Задание температуры окружающей среды t_с и усло­вий теплообмена α между средой и поверхностью в функции времени и координат называется граничным условием III рода. Так как, плотность теплового по­тока, поступающего на поверх­ность тела, равна

q = α ( t_с - t ) , (57)

а тепловой поток, поступающий с поверхности внутрь тела,

q = - λ grаd t, (58)

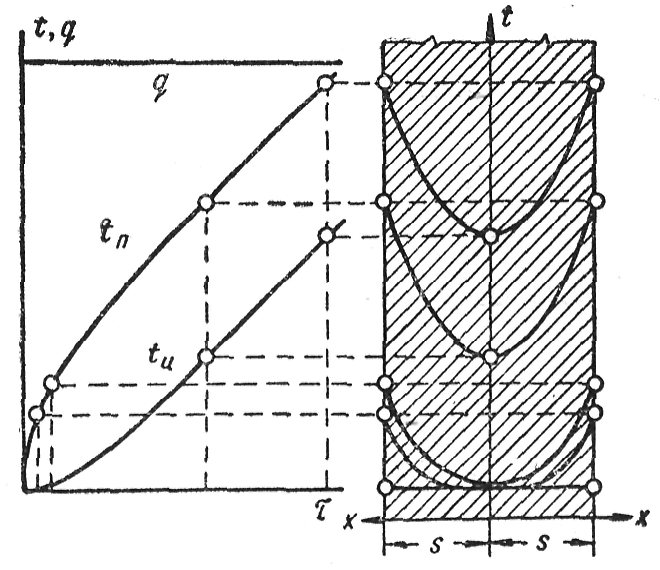
Рис.16 Нагрев пластины при постоянном тепловом потоке через ее поверхность ( граничные условия II рода)

то граничное условие III рода записывается так:

α ( t_с - t ) = - λ grаd t (59)

Процессы нагрева, при которых целесообразно применять гра­ничное условие III рода, встречаются весьма часто. Один из примеров - нагрев заготовки в печи с постоянной температурой.

Нагрев пластины протекает так, как показано на рис.17. В начале нагрева температура на поверхности поднимается бы­стрее, чем в центре. По мере уменьшения разности температур среды и поверхности удельный тепловой поток уменьшается, нагрев замедляется. В результате длительной выдержки темпе­ратура по всему сечению пластины будет равна температуре среды.

Аналитическое решение уравнения (59) возможно лишь при простейших краевых условиях, но даже в этом случае фор­мулы получаются весьма сложными, поэтому при технических расчетах нестационарной теплопроводности обычно пользуются специальными графиками и таблицами. Чтобы сократить число величин, описывающих нагрев, их группируют в безразмерные комплексы, пользуясь методами теории подобия.

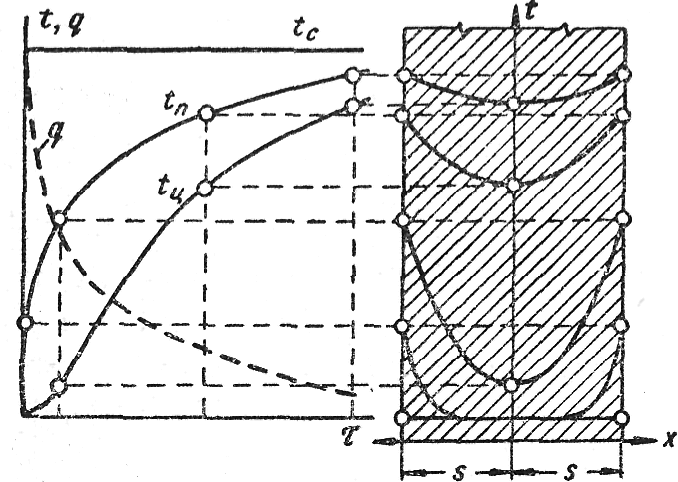
Рис. 17. Нагрев пластины при передаче тепла конвекцией от среды с постоянной температурой

Сформулируем задачу математически. За начало отсчета тем­ператур примем температуру среды. Тогда всякая другая тем­пература будет выражаться как Для бесконечной пластины, температурное поле которой изменяется только вдоль оси х, уравнение Фурье (56) примет вид

(60)

начальное условие х = 0,  = _н, (61)

граничное условие для симметричного нагрева, согласно уравнению (59):

(62)

Приведя выражения (60) - (62) к безразмерному виду, получим зависимость безразмерной температуры от безразмерных коэффициента тепло­отдачи, времени и координаты:

, или

(63)

Безразмерный коэффициент теплоотдачи А называется критерием Био (Вi = ). Безразмерное время называется критерием Фурье (Fо = ).

Для нагрева тел простейшей формы (бесконечная пластина, бесконечный цилиндр, шар) при граничных условиях III рода имеется аналитическое решение в виде зависимости (63), но, так как оно громоздко, в технических расчетах часто пользуются спе­циальными графиками для безразмерной температуры центра

(64)

и поверхности

(65)

Графики такого типа, составленные Д. В. Будриным, при­ведены на рис. 47-50. Для определения безразмерной темпера-туры при малых значениях критерия Фурье следует пользоваться графиками Будрина - Красовского (рис. 22-25).

По этим номограммам можно решить две задачи – прямую и обратную. В соответствии с прямой задачей необходимо определить время нагрева т.е. критерий Fо, в который входит τ. Отсюда путь решения при заданных параметрах нагрева - вычисляем из условий нагрева критерии Вi и Θ_п, а по номограммам находим Fо, из которого вычисляем время нагрева τ.

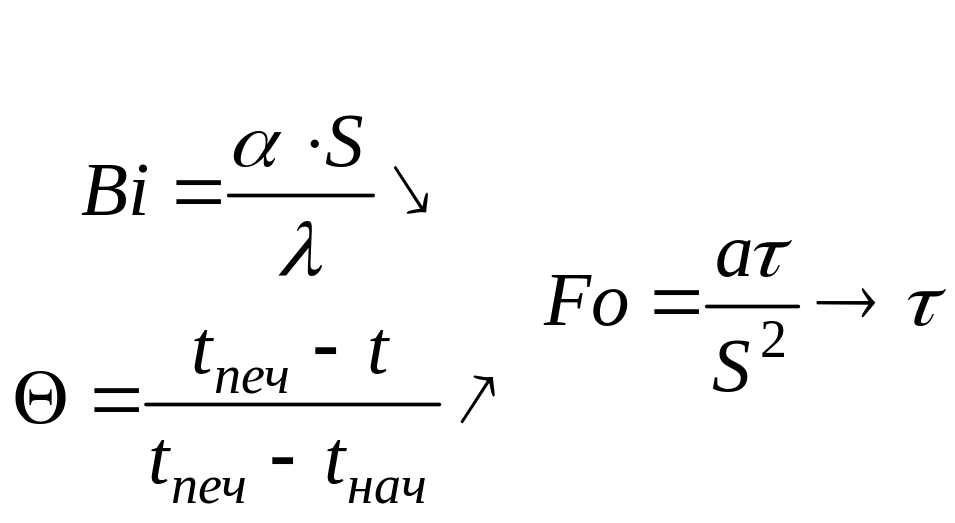
При постановке обратной задачи по заданному времени нагрева, определить температуру нагрева. Отсюда путь решения

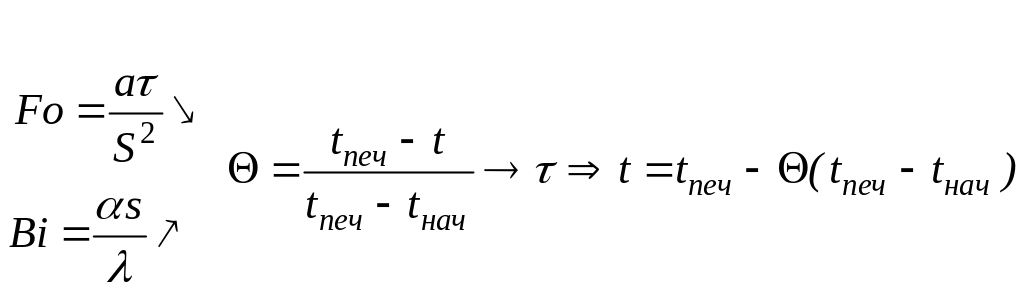
Т.е. если задано время нагрева τ, то можно вычислить критерий Fо. Из условий нагрева Вi вычисляем критерий Θ, из которого вычисляем температуру нагрева.