Составление математической модели задачи

1. Исходя из содержательной постановки задачи и характера исходных данных, очевидно, что задача относится к классу задач рационального использования ресурсов. Сведем исходные данные в типовую таблицу, характерную для данного класса задач:

Таблица 2.2. Типовая таблица исходных данных

Сырьё	Запас сырья, т.у.т.	Норма расхода сырья, т.у.т./МВт*ч
		ТЭС 1	ТЭС 2	ТЭС 3	ТЭС 4
Кам. уголь	150	5	1	6	6
Бур. уголь	85	1	5	5	1
Газ	190	5	6	3	3
Мазут	123	2	5	1	4
Стоимость электроэнергии на ТЭС, у.е./МВт*ч		20	15	18	18

2. Введем обозначения искомых переменных.

Оптимальный план отпуска электроэнергии складывается из:

х₁ –отпуск электроэнергии на ТЭС 1, МВт*ч;

х₂ –отпуск электроэнергии на ТЭС 2, МВт*ч;

х₃ –отпуск электроэнергии на ТЭС 3, МВт*ч;

х₄ –отпуск электроэнергии на ТЭС 4, МВт*ч;

3. Составим математическую модель (ММ):

Ц.Ф.: F(x)=20x₁+15x₂+18х₃+18х₄→max

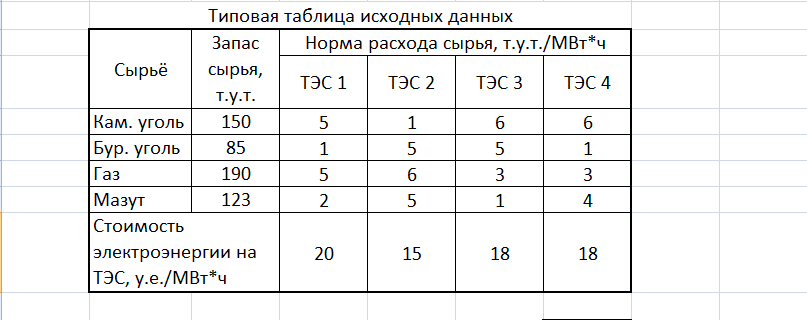
О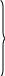 ГР: 5x₁+x₂+6х₃+6х₄ ≤ 150

ограничения по запасу топлива

x₁+5x₂+5х₃+х₄ ≤ 85

5x₁+6x₂+3х₃+3х₄ ≤ 190

2x₁+5x₂+х₃+х₄ ≤ 123

ГРУ: х₁ ≥ 0, х₂ ≥ 0, х₃ ≥ 0, х₄ ≥ 0

Решение задачи с помощью надстройки «Поиск решения» среды Microsoft Excel

Таким образом, найдено следующее решение:

х₁=20,39 МВт*ч отпуск электроэнергии на ТЭС 1;

х₂=11,64 МВт*ч отпуск электроэнергии на ТЭС 2;

х₃=0,08 МВт*ч отпуск электроэнергии на ТЭС 3;

х₄=5,98 МВт*ч отпуск электроэнергии на ТЭС 4;

F(x)=691,64 у.е. – доход от реализации электроэнергии.

Поскольку все ограничения равны максимально допустимым значениям, то излишков сырья (топлива) нет.

ВЫВОД

Широкий класс оптимизационных задач может быть решен при помощи методов линейного программирования. При этом основной особенностью таких задач является то, что математическая модель целиком описывается при помощи линейных зависимостей.

При малых размерностях задачи линейного программирования (n=2) можно использовать графический метод. Его главным достоинством является наглядность представления решения на плоскости, что позволяет не только определить точку оптимального решения, но и отсутствие решения, а также наличие альтернативного решения. Недостатком метода является серьезная погрешность результата и невозможность решения при больших размерностях задачи.

При больших размерностях (n>2) используется симплекс-метод. Аналитическая его реализация позволяет наглядно представить все этапы решения и промежуточные результаты (текущее решение), но требует громоздких и трудоемких вычислений. Табличная реализация симплекс-метода позволяет существенно сократить объем вычислений, а специфический метод расчета – существенно их упростить. Компьютерная реализация табличного симплекс-метода дает наиболее точный результат и требует наименьшего времени расчета, однако не дает полного представления об этапах и принципах расчетов.

Таким образом, каждый метод линейного программирования может быть использован в той или иной ситуации, исходя из того, какого рода результат необходимо получить.