Решение задачи симплекс-методом (табличная реализация)

ММ в стандартной форме (из расчетов, произведенных выше):

3 х₁+7х₂+х₃ = 2100;

5

(6)

х₁+6х₂+х₄ = 3000;

-100x₁-200x₂= F(x)

х₁ ≥ 0, х₂ ≥ 0, х₃ ≥ 0, х₄ ≥ 0

Произведем решение задачи по стандартному алгоритму:

Этап 1. Начальное приближение – опорное решение.

х свободные переменные 1=0	х базис 3≠0
х2=0	х4≠0

Используя систему (6) выразим базисные переменные через свободные:

х3=	2100	- (7) (3х1+7х2)
х4=	3000	-(5х1+6х2)
F(x)=	0	-(100x1+200x2)

базис решение свободные переменные

Используя систему уравнений (7), представим начальную симплекс-таблицу:

Таблица 1.3. Исходная симплекс-таблица

Ц.Ф. Базис	Свободные члены уравнений	Свободные переменные
		-х1	-х2
F(x)	0	100	200
х3	2100	3	7	2100/7=300→min
х4	3000	5	6	3000/6=500

Опорное решение:

х свободные переменные 1=0	х базис F(x)=0 3=2100
х2=0	х4=3000

Анализ решения:

Исходя из правил анализа симплекс-таблиц текущего решения, опорное решение допустимое, т.к. х_i ≥ 0, i=1…4, но не оптимальное, т.к. все коэффициенты в Ц.Ф. положительные.

Этап 2. Первая итерация, i=1.

Ц.Ф. Базис	Свободные члены уравнений	Свободные переменные
		-х1	-х2
F(x)	0	100	200 (-λ)
	-60060	-85,8	-28,6
х3	2100 (λ)	3 (λ)	7
	300,3	0,429	λ=0,143
х4	3000	5	6 (-λ)
	-1801,8	-2,574	-0,858

Данная таблица была получена путем преобразования исходной симплекс-таблицы (табл. 1.3.) следующим образом:

• разрешающий столбец: -х₂ (т.к. 200>100)

• разрешающая строка: х₃ (т.к. 300<500)

• генеральный коэффициент: λ= 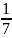=0,143

• в разрешающую строку снизу занесены произведения верхних коэффициентов на (λ), а в разрешающий столбец – на (-λ)

• произведено заполнение остальных клеток по правилам работы с симплекс-таблицами

Далее произведем сложение верхних и нижних коэффициентов в невыделенных клетках, а в выделенных – оставим только нижние коэффициенты. Коэффициенты х₂ и х₃ в выделенных столбце и строке поменяются местами. В результате получим симплекс-таблицу текущего решения:

Таблица 1.4. Симплекс-таблица текущего решения №1

Ц.Ф. Базис	Свободные члены уравнений	Свободные переменные
		-х1	-х3
F(x)	-60060	14,2	-28,6
х2	300,3	0,429	0,143	300,3/0,429=700
х4	1198,2	2,426	-0,858	1198,2/2,426=493,9→min

Текущее решение:

х свободные переменные 1=0	х базис F(x)=-60060 2=300,3
х3=0	х4=1198,2

Анализ решения:

Решение допустимое, т.к. х_i ≥ 0, i=1…4.

Решение не оптимальное, т.к. в Ц.Ф. есть положительный коэффициент при (-х₁) и при увеличении х₁ произойдет снижение F(x), т.е. F(x) – не минимальное.

Этап 3. Вторая итерация, i=2.

Ц.Ф. Базис	Свободные члены уравнений	Свободные переменные
		-х1	-х3
F(x)	-60060	14,2 (-λ)	-28,6
	-7009,47	-5,85	-5,02
х2	300,3	0,429 (-λ)	0,143
	-212,08	-0,177	0,15
х4	1198,2 (λ)	2,426	-0,858 (λ)
	493,66	λ=0,412	-0,35

Данная таблица была получена путем преобразования симплекс-таблицы текущего решения (табл. 1.4.) следующим образом:

• разрешающий столбец: -х₁ (т.к. 14,2>0)

• разрешающая строка: х₄ (т.к. 493,9<700)

• генеральный коэффициент: λ= 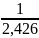=0,412

• в разрешающую строку снизу занесены произведения верхних коэффициентов на (λ), а в разрешающий столбец – на (-λ)

• произведено заполнение остальных клеток по правилам работы с симплекс-таблицами

Далее произведем сложение верхних и нижних коэффициентов в невыделенных клетках, а в выделенных – оставим только нижние коэффициенты. Коэффициенты х₁ и х₄ в выделенных столбце и строке поменяются местами. В результате получим симплекс-таблицу текущего решения:

Таблица 1.5. Симплекс-таблица текущего решения №2

Ц.Ф. Базис	Свободные члены уравнений	Свободные переменные
		-х4	-х3
F(x)	-67069,47	-5,85	-33,62
х2	88,22	-0,177	0,29
х1	493,66	0,412	-0,35

Решение:

х отсутствие резерва по сырью 3=0
х4=0

х₁=493,66 кг - производство краски А;

х₂=88,22 кг - производство краски В;

F=-F=67069,47 у.е. - доход от реализации краски.

Анализ решения:

Решение допустимое, т.к. х_i ≥ 0, i=1…4.

Решение оптимальное, т.к. все коэффициенты в Ц.Ф. отрицательные и увеличение переменных х₃ и х₄ не приведет к дальнейшему снижению F(x), т.е. F(x) – минимальное.

Таким образом, полученная симплекс-таблица (табл. 1.5.) является итоговой.