
- •6. Cиловой расчет механизма двигателя
- •6.1. Определение ускорений точек и звеньев механизма
- •6.2. Задачи силового расчета
- •6.3. Силы, действующие в механизме
- •6.4. Силовой расчет структурной группы 2-3
- •6.4. Силовой расчет структурной группы 4-5
- •6.5. Силовой расчет исходного механизма
- •6.6. Метод н.Е. Жуковского
6.4. Силовой расчет структурной группы 4-5
В
соответствие с формулой строения
механизма структурная группа 4-5
присоединяется к исходному механизму
– звену 1. Структурная группа 4-5
вычерчивается отдельно на чертеже в
соответствующем масштабе l
в заданном положении. К звеньям группы
прикладывают внешние силы и моменты –
 ,
,
 ,
,
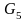 ,
,
 ,
,
 ,
,
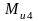 .
Эти силы и моменты известны по величине
и по направлению. Как указывалось ранее,
действием отброшенных звеньев кривошипа
1 и стойки 0 заменяют реакциями
и
.
Реакция во вращательной паре А
неизвестна по величине и по направлению.
Реакция в поступательной паре Вх
(поршень-стойка)
является неизвестной по величине и
известной по направлению – реакция
перпендикулярна к оси цилиндра х-х.
.
Эти силы и моменты известны по величине
и по направлению. Как указывалось ранее,
действием отброшенных звеньев кривошипа
1 и стойки 0 заменяют реакциями
и
.
Реакция во вращательной паре А
неизвестна по величине и по направлению.
Реакция в поступательной паре Вх
(поршень-стойка)
является неизвестной по величине и
известной по направлению – реакция
перпендикулярна к оси цилиндра х-х.
На структурную группу 4-5 (рис.6.6) действуют внешние силы, силы инерции и реакции отброшенных звеньев, согласно принципу Д’Аламбера находится в равновесии. Условие равновесия структурной группы: векторная сумма всех сил действующих на систему тел равна нулю, т.е. . Уравнение равновесия структурной группы
 .
(6.8)
.
(6.8)
Реакции
во внутренней кинематической паре D
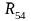 и
и
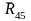 в этом уравнении отсутствую, поскольку
они друг друга уравновешивают
в этом уравнении отсутствую, поскольку
они друг друга уравновешивают
 .
В уравнение (6.8) неизвестными оказываются
два слагаемых – реакции
и
.
Чтобы частично раскрыть неопределенность
с реакцией
,
ее раскладывают на тангенциальную
.
В уравнение (6.8) неизвестными оказываются
два слагаемых – реакции
и
.
Чтобы частично раскрыть неопределенность
с реакцией
,
ее раскладывают на тангенциальную
 и нормальную
и нормальную
 составляющие
составляющие
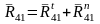 .
.
В результате уравнение (6.8) примет вид
 .
(6.9)
.
(6.9)
Тангенциальная
реакция
вычисляется из условия равновесия звена
4 – это звено по принципу Д’Аламбера
находится в равновесии. Для этого
составляется уравнение моментов
относительно точки В
 . Предварительное направление
. Предварительное направление
 может выбрано произвольным, так как
истинное направление определит знак
этой реакции: «плюс» – предварительное
направление оказалось правильным,
«минус» – следует изменить направление
реакции на противоположное.
может выбрано произвольным, так как
истинное направление определит знак
этой реакции: «плюс» – предварительное
направление оказалось правильным,
«минус» – следует изменить направление
реакции на противоположное.
 .
.
Тогда
 ,
,
где – масштаб, в котором вычерчена структурная группа на чертеже, м/мм;
 ,
,
 –плечи сил (мм),
определяются из чертежа.
–плечи сил (мм),
определяются из чертежа.
Примечание: значение силы имеет положительный знак.
В
итоге в уравнении (6.9) остаются две
неизвестными реакции –
и
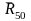 неизвестны по величине и известны по
направлению. В уравнении (6.9) это отмечено
подчеркиванием и знаком вопроса, силы,
которые полностью определены по величине
и направлению действия отмечены двойным
подчеркиванием.
неизвестны по величине и известны по
направлению. В уравнении (6.9) это отмечено
подчеркиванием и знаком вопроса, силы,
которые полностью определены по величине
и направлению действия отмечены двойным
подчеркиванием.
Для нахождение неизвестных реакций и строится план сил. Для этого определяется масштабный коэффициент плана сил (Н/мм). Далее рассчитываются отрезки, которые будут изображать на плане сил известные силы уравнения (6.9):
|
|
|
|
|
|
Из начальной точки pF (рис. 6.6), полюса плана сил, откладывают отрезки , , , , , в соответствии с направлениями этих сил. Далее согласно формуле (6.9) из полюса pF проводится прямая параллельная звену СD – линия действия реакции , а из последней точки f проводится прямая параллельная оси цилиндра x-x (рис. 6.6)– линия действия реакции . Эти линии пересеклись в точке g и определили искомые реакции.

Рис.6.6. Построение плана сил структурной группы 4-5
Из плана сил находят величины реакций
 ,
,
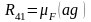 ,
,
 .
.
Реакцию во внутренней кинематической паре D, образованная звеньями 4 и 5, определяют из уравнения равновесия сил, действующих на поршень 5. По принципу Д’Аламбера звено 5 находится в равновесии – векторная сумма всех сил равна нулю
 (6.10)
(6.10)
Реакция
 ,
которая неизвестна по величине и по
направлению, определяется из плана сил,
построенного по уравнению (6.10) как
результирующий замыкающий вектор. План
сил звена 5 (рис.6.6) следует проводить в
том же масштабе
(Н/мм),
что и план сил структурной группы 4-5.
Рассчитываются отрезки, которые будут
изображать на плане сил известные силы
уравнения (6.10):
,
которая неизвестна по величине и по
направлению, определяется из плана сил,
построенного по уравнению (6.10) как
результирующий замыкающий вектор. План
сил звена 5 (рис.6.6) следует проводить в
том же масштабе
(Н/мм),
что и план сил структурной группы 4-5.
Рассчитываются отрезки, которые будут
изображать на плане сил известные силы
уравнения (6.10):
 мм;
мм;
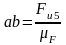 мм
мм
 мм
,
мм
,
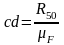 мм
.
мм
.
Из
плана сил находится величина реакции
 . Согласно третьему закону Ньютона
. Согласно третьему закону Ньютона
 .
.

 мм;
мм;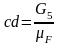 мм;
мм; мм;
мм; мм;
мм; мм;
мм;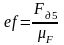 мм.
мм.