
- •6. Cиловой расчет механизма двигателя
- •6.1. Определение ускорений точек и звеньев механизма
- •6.2. Задачи силового расчета
- •6.3. Силы, действующие в механизме
- •6.4. Силовой расчет структурной группы 2-3
- •6.4. Силовой расчет структурной группы 4-5
- •6.5. Силовой расчет исходного механизма
- •6.6. Метод н.Е. Жуковского
6. Cиловой расчет механизма двигателя
6.1. Определение ускорений точек и звеньев механизма
Последовательность построение плана ускорений (как и плана скоростей) определяется формулой строения механизма: сначала строим для кривошипа АОС, затем для структурных групп 2-3 и 4-5.
Кривошип
1 не движется равномерно: в каких-то
моментах он будет двигаться или ускоренно
или замедленно,
 ,
,
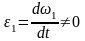 ,
поэтому ускорение точки А
представляет собой векторную сумму
ускорений
,
поэтому ускорение точки А
представляет собой векторную сумму
ускорений
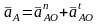 м/с2,
м/с2,
где
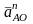 – нормальное ускорение точки А
вокруг точки О;
– нормальное ускорение точки А
вокруг точки О;
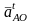 – тангенциальное
ускорение точки А
вокруг точки О.
– тангенциальное
ускорение точки А
вокруг точки О.
Нормальное ускорение определяется по формуле
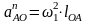 м/с2,
м/с2,
где
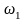 – угловая
скорость кривошипа в рассматриваемом
положении, с-1,
табл. 5.11;
– угловая
скорость кривошипа в рассматриваемом
положении, с-1,
табл. 5.11;
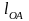 – длина
кривошипа, м.
– длина
кривошипа, м.
Ускорение
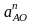 направлено
вдоль звена ОА
к центру вращения точке, т.е. от точки А
к точке О
(рис. 6.1).
направлено
вдоль звена ОА
к центру вращения точке, т.е. от точки А
к точке О
(рис. 6.1).
Касательное ускорение вычисляется по уравнению
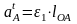 м/с2,
м/с2,
где
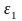 – угловое
ускорение кривошипа в рассматриваемом
положении, с-2
.
– угловое
ускорение кривошипа в рассматриваемом
положении, с-2
.
Угловое ускорение определяется по уравнению движения машинного агрегата в дифференциальной форме
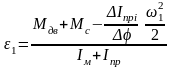 с-2, (6.1)
с-2, (6.1)
где Mдв, Mс – моменты движущих сил (табл.5.7) и сил сопротивления (табл.5.8), Нм;
Iпр
– приращение приведенного момента
инерции, кг,
 ;
;
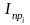 ,
,
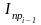 –
приведенные моменты инерции в текущем
и предыдущем положении кривошипа, кгм2;
–
приведенные моменты инерции в текущем
и предыдущем положении кривошипа, кгм2;
– приращение
угла поворота кривошипа,
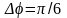 ,
рад;
,
рад;
1 – угловая скорость кривошипа в данном положении табл. 5.11, с-1;
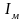 – момент
инерции маховика.
– момент
инерции маховика.
Масштабный коэффициент плана ускорений рассчитывается по формуле
 м/с2/(мм),
м/с2/(мм),
где
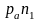 – длина отрезка, изображающего на плане
ускорений нормальное ускорение точки
,
pan1=70…80
мм.
– длина отрезка, изображающего на плане
ускорений нормальное ускорение точки
,
pan1=70…80
мм.
Отрезок
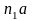 ,
который изображает на плане ускорений,
ускорение
,
который изображает на плане ускорений,
ускорение
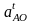 рассчитывается по формуле
рассчитывается по формуле
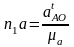 мм.
мм.
Для определения ускорения точки В воспользуемся уравнением Эйлера
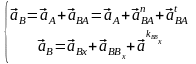 (6.2)
(6.2)
где
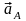 – переносное
ускорение точки А;
– переносное
ускорение точки А;
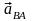 – относительное
ускорение точки В
вокруг А,
это ускорение раскладывается на две
составляющие –
– относительное
ускорение точки В
вокруг А,
это ускорение раскладывается на две
составляющие –
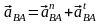 ,
,
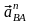 – относительное
нормальное ускорение точки В
вокруг точки А,
оно известно по абсолютной величине и
по направлению: направлено параллельно
звену AB,
от точки В
к точке А
(т.В
т.А)
(рис.6.1), численное значение этого
ускорения вычисляется по равенству
– относительное
нормальное ускорение точки В
вокруг точки А,
оно известно по абсолютной величине и
по направлению: направлено параллельно
звену AB,
от точки В
к точке А
(т.В
т.А)
(рис.6.1), численное значение этого
ускорения вычисляется по равенству
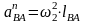 ,
,
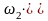 –
угловая
скорость звена 2,указана в табл. 4.1.
–
угловая
скорость звена 2,указана в табл. 4.1.
На
плане ускорений ускорение
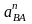 отображается в виде отрезка
отображается в виде отрезка
 ,
величина которого равна
,
величина которого равна
 мм;
мм;
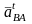 – относительное
тангенциальное ускорение точки В
вокруг точки А,
оно неизвестно по абсолютной величине
и известно по направлению: направлено
перпендикулярно звену AB;
– относительное
тангенциальное ускорение точки В
вокруг точки А,
оно неизвестно по абсолютной величине
и известно по направлению: направлено
перпендикулярно звену AB;
аВх – ускорение точки в переносном вращательном движении с направляющей х-х, аВх=0;
аВBх – ускорение точки В в поступательном движении относительно точки Вх, оно направлено параллельно оси х-х;
акВВх – относительное кориолисово ускорение, акВВх=0.
Построение
плана ускорений структурной группы 2-3
производится в такой последовательности
(рис. 6.1): из произвольно выбранной точки
pa
– полюса плана скоростей, проводим
отрезок
(изображает ускорение
)
параллельно звену ОА
от точки А
к точке О.
Из точки
 строится отрезок
(изображает ускорение
),
его направление определяется направлением
углового ускорения
.
Далее строится вектор полного ускорения
строится отрезок
(изображает ускорение
),
его направление определяется направлением
углового ускорения
.
Далее строится вектор полного ускорения
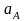 – отрезок
– отрезок
 .
После этого согласно первому уравнению
системы (1) из точки а
откладываем вектор
(изображает ускорение
),
затем из полученной точки
.
После этого согласно первому уравнению
системы (1) из точки а
откладываем вектор
(изображает ускорение
),
затем из полученной точки
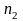 проводим прямую перпендикулярную звену
АВ,
которая является линией действия
неизвестного по величине тангенциального
ускорения
.
Все слагаемые из первого уравнения
системы (6.2) использованы, поэтому
переходим ко второму уравнению. В этом
уравнении осталось неравным нулю только
относительное ускорение аВBх,
о котором на данном этапе известно
только его направление. В связи с этим
из полюса pa
проводим прямую параллельную оси
цилиндра х-х.
Данная и проведенная раннее прямые
пересеклись, тем самым определили
решение уравнений – точку b.
На основании построенного плана получили
значения ускорений
проводим прямую перпендикулярную звену
АВ,
которая является линией действия
неизвестного по величине тангенциального
ускорения
.
Все слагаемые из первого уравнения
системы (6.2) использованы, поэтому
переходим ко второму уравнению. В этом
уравнении осталось неравным нулю только
относительное ускорение аВBх,
о котором на данном этапе известно
только его направление. В связи с этим
из полюса pa
проводим прямую параллельную оси
цилиндра х-х.
Данная и проведенная раннее прямые
пересеклись, тем самым определили
решение уравнений – точку b.
На основании построенного плана получили
значения ускорений
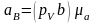 ,
,
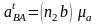 ,
,
и углового ускорения звена 2
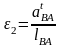 .
.
Чтобы
определить направление углового
ускорения
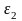 ,
следует мысленно разметить вектор
в точку В.
Направление вращения этого вектора
относительно точки А
определит направление углового ускорения
.
,
следует мысленно разметить вектор
в точку В.
Направление вращения этого вектора
относительно точки А
определит направление углового ускорения
.

Рис.6.1. Построение плана ускорений структурной группы 2-3
Для
нахождения ускорения центра тяжести
S2
звена AB
необходимо определить полное ускорение
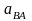 ,
соединив при этом точки а
и b
на плане ускорений. Используя отношение
,
соединив при этом точки а
и b
на плане ускорений. Используя отношение
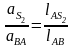 или
или
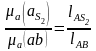
Откуда определяется
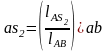
На плане ускорений откладываем отрезок аs2 и соединяем полученную точку s2 с полюсом pa. Отрезок pas2 изобразит на плане ускорение аS2
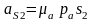 .
.
Определяем ускорения структурной группы 4-5. ускорение точки С представляет собой векторную сумму ускорений
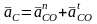 ,
,
где
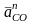 – нормальное ускорение точки С
вокруг точки О;
– нормальное ускорение точки С
вокруг точки О;
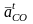 – тангенциальное
ускорение точки С
вокруг точки О.
– тангенциальное
ускорение точки С
вокруг точки О.
Нормальное ускорение определяется по формуле
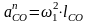 м/с2,
м/с2,
где – угловая скорость кривошипа в рассматриваемом положении, с-1, табл. 5.11;
 – длина
кривошипа, м.
– длина
кривошипа, м.
Ускорение
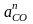 направлено
вдоль звена ОС
к центру вращения точке, т.е. от точки С
к точке О
(рис. 6.1).
направлено
вдоль звена ОС
к центру вращения точке, т.е. от точки С
к точке О
(рис. 6.1).
Касательное ускорение вычисляется по уравнению
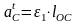 м/с2,
м/с2,
где – угловое ускорение кривошипа в рассматриваемом положении, с-2 , формула (6.1).
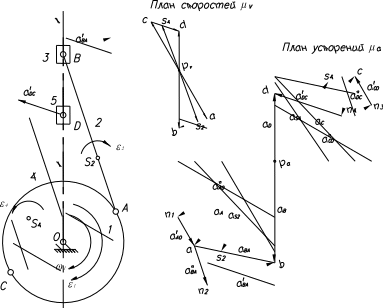
Рис.6.2. План ускорений механизма
Величина отрезка, который представляет на плане ускорений ускорение вычисляется как
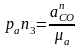 мм,
мм,
Отрезок
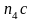 ,
который изображает на плане ускорений,
ускорение
,
который изображает на плане ускорений,
ускорение
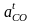 рассчитывается по формуле
рассчитывается по формуле
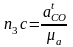 мм.
мм.
Для определения ускорения точки D воспользуемся уравнением Эйлера
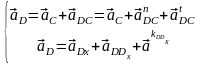 (6.3)
(6.3)
где
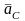 – переносное
ускорение точки C;
– переносное
ускорение точки C;
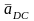 – относительное
ускорение точки D
вокруг C,
это ускорение раскладывается на две
составляющие –
– относительное
ускорение точки D
вокруг C,
это ускорение раскладывается на две
составляющие –
 ,
,
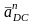 – относительное
нормальное ускорение точки D
вокруг точки C,
оно известно по абсолютной величине и
по направлению: направлено параллельно
звену CD,
от точки D
к точке C
(т.D
т.C)
(рис.6.2), численное значение этого
ускорения вычисляется по равенству
– относительное
нормальное ускорение точки D
вокруг точки C,
оно известно по абсолютной величине и
по направлению: направлено параллельно
звену CD,
от точки D
к точке C
(т.D
т.C)
(рис.6.2), численное значение этого
ускорения вычисляется по равенству
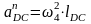 ,
,
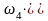 –
угловая
скорость звена 4,указана в табл. 4.1.
–
угловая
скорость звена 4,указана в табл. 4.1.
На
плане ускорений ускорение
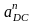 отображается в виде отрезка
отображается в виде отрезка
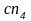 ,
величина которого равна
,
величина которого равна
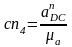 мм;
мм;
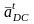 – относительное
тангенциальное ускорение точки D
вокруг точки C,
оно неизвестно по абсолютной величине
и известно по направлению: направлено
перпендикулярно звену CD;
– относительное
тангенциальное ускорение точки D
вокруг точки C,
оно неизвестно по абсолютной величине
и известно по направлению: направлено
перпендикулярно звену CD;
aDх – ускорение точки в переносном вращательном движении с направляющей х-х, аDх=0;
аDDх – ускорение точки D в поступательном движении относительно точки Dх, оно направлено параллельно оси х-х;
акDDх – относительное кориолисово ускорение, акDDх=0.
Построение плана ускорений структурной группы 4-5 производится аналогично плану ускорений структурной группы 4-5. На основании построенного плана получили значения ускорений
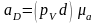 ,
,
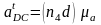 ,
,
и углового ускорения звена 4
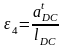 .
.
Чтобы
определить направление углового
ускорения
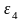 ,
следует мысленно разметить вектор
в точку D.
Направление вращения этого вектора
относительно точки C
определит направление углового ускорения
.
,
следует мысленно разметить вектор
в точку D.
Направление вращения этого вектора
относительно точки C
определит направление углового ускорения
.
Для
нахождения ускорения центра тяжести
S4
звена CD
необходимо определить полное ускорение
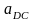 ,
соединив при этом точки c
и d
на плане ускорений. Используя отношение
,
соединив при этом точки c
и d
на плане ускорений. Используя отношение
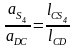 или
или
 .
.
Откуда определяется
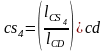 мм.
мм.
На плане ускорений откладываем отрезок сs4 и соединяем полученную точку s4 с полюсом pa. Отрезок pas4 изобразит на плане ускорение аS4
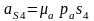 м/с2.
м/с2.
