Определение приведенных моментов инерции механизма

№ положения	1, грд	, кгм2	, кгм2	, кгм2	, кгм2	, кгм2	, кгм2
0	0
1	30
2	60
….	….
23	690
24	720

Масштаб оси ординат диаграммы приведенных моментов инерции механизма определяется по равенству

,

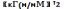где 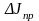– максимальное приращение приведенного момента инерции механизма, кг;

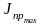– максимальное значение приведенного момента инерции, указано в табл. 5.10;

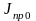– приведенный момент инерции механизма в 0-вом положении;

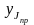– отрезок, который изображает на диаграмме 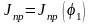максимальное приращение момента инерции , его следует принять =100…110 мм.

Для построения диаграммы приведенных моментов инерции необходимо определить отрезки, которые будут изображать на этой диаграмме приведенные моменты инерции в соответствующих положениях кривошипа 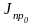, , 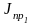, 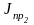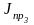…, , 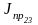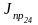(табл. 5.10)

, , …. , .

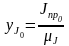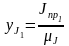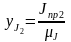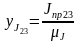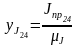По подсчитанным данным строится диаграмма приведенных моментов инерции механизма (рис. 5.9).

5.5. Определение потребного момента инерции маховика

Определение потребного момента инерции маховика будем производить методом профессора Виттенбауэра. В соответствии с этим методом строится диаграмма зависимости 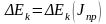, так называемая диаграмма «энергия-масса». Для этого на основании диаграмм и 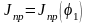путем исключения аргумента 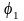строится диаграмма – точки 0, 1, 2, 3, 4, 5 …. 20, 21, 22, 23, 24 этой диаграммы получаются путем переноса ординат соответствующих точек диаграмм и _.

Рис. 5.9. Построение диаграммы приведенных моментов инерции механизма и диаграммы «энергия-масса» (диаграммы Виттенбауэра)

Вычисляются максимальная и минимальная скорости кривошипа за цикл

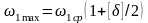, (5.9)

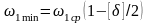, (5.10)

где 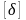– допустимое значение коэффициента неравномерности движения.

К полученной диаграмме «энергия – масса» проводим две касательные прямые под углами, тангенсы которых равны

,

,

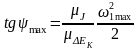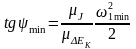_J, _Ek – масштабные коэффициенты оси абсцисс и оси ординат диаграммы Витенбауэра, 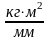и .

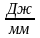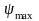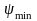Две касательные и пересекут ось ординат 0E_k в точках a и b (рис. 5.9). Измерив отрезок ab (мм), удается определить потребный момент инерции маховика по зависимости

,

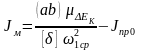где – приведенный момент инерции механизма в 0-вом положении.

При углах и близких к 90 касательные могут не пересекать ось оси ординат диаграммы в пределах чертежа. В таком случае отрезок определяется из такого соотношения (рис. 5.10):

,

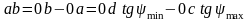где 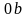, 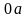– отрезки, которые отсекают по оси абсцисс касательные, проведенные под углами и .

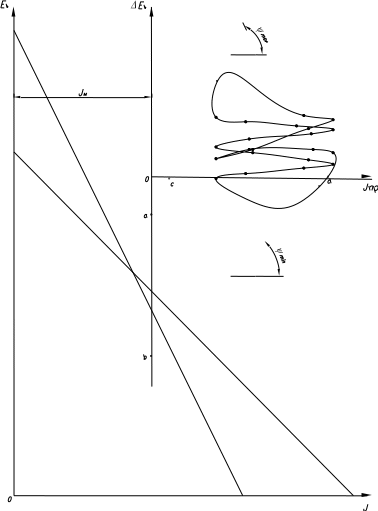
Рис. 5.10. Определение момента инерции маховика при больших углах и

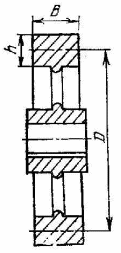
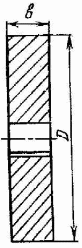
После определения момента инерции маховика необходимо вычислить его основные размеры. Маховик может быть изготовлен в виде колеса со спицами (рис. 5.11 а) и сплошного диска (рис. 5.11 б).

Если маховик выполнен в виде колеса со спицами (рис. 5.11 а), момент инерции обода составляет при мерно 90% момента инерции всего маховика. Предполагая, что масса обода 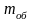равномерно распределена по окружности среднего диаметра обода D, можно использовать формулу для определения момента инерции тонкого кольца

,

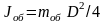где – масса обода 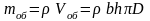кг,

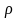– плотность материала, для чугунных маховиков =7000 кг/м³, для стальных маховиков =7800 кг/м³,

b – ширина обода маховика м,

h – толщина обода маховика м.

При проектировании маховика обычно определяют средний диаметр, а ширину и толщину учитываю через коэффициенты и 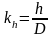, поэтому средний диаметр маховика следует рассчитать из выражения

.

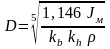Коэффициенты 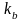и 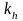как правило выбирают в пределах 0,1…0,3. Масса маховика равна .

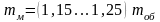Если маховик выполняется в виде сплошного диска (рис. 5.11 б), можно использовать формулу для момента инерции цилиндра 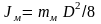. Из этой формулы с учетом того, что 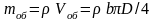и задаваясь отношением ,

находим

.

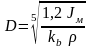После ориентировочного определения размеров маховика и для окончательного выбора его конструкции (рис. 11), следует рассчитать окружную скорость обода маховика

,

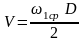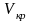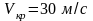поскольку она не должна превышать критической скорости , допускаемой по условию прочности на разрыв центробежными силами инерции. Для чугунных маховиков , стальных .

а)

б)

Рис. 5.11. Конструкции маховиков