3.2. Проектирование балки из заданного материала.

Для построений эпюр ЭQ И ЭМ найдем опорные реакции

Отсюда

Найдем Реакцию в опоре В

Эпюра ЭQ

Q_AB=-4qa

Qb= Q_AB+Rb=-4qa+7.166qa=3.166qa

Q’c= Q_B-q*3a=3.166qa-q*3a=0.166qa

Q”c= Q’c+Rc=0.166qa-0.166qa=0

Эпюра ЭМ

Ма=0

Мв=Ма-4qa*a=0-4qa*a=-4qa*a

Mcd=qaa

Согласно эпюрам максимальный изгибающий момент возникает в сечении В, где Мив=-4qaa=-4*10*1*1=-40кНм

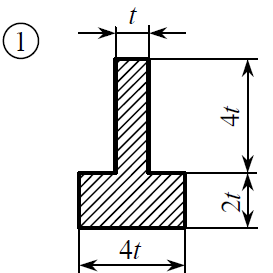
Геометрические характеристики сечения

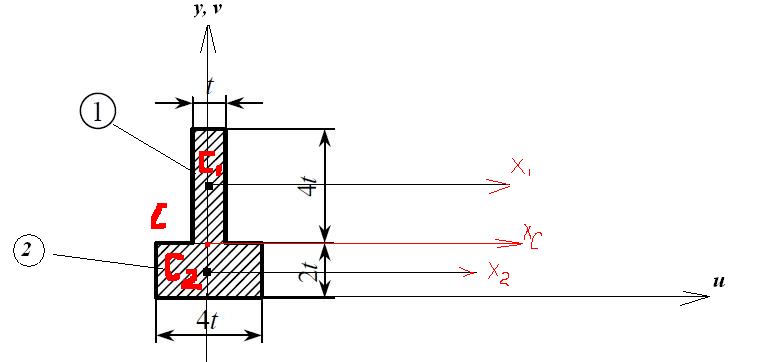
1. Положение центра тяжести

№ фигуры	Координата v	Площадь сечения А	Произведение v*A
1	4t	4t2	16 t3
2	1t	8t2	8t3
		12t2	24t3

Тогда положение центра тяжести

2. Момент инерции относительно главной центральной оси

Предварительно определим моменты инерции для элементов сечения относительно собственных центральных осей, а последующие вычисления выполним в табличной форме

№ фигуры	yi=vc-vi	Площадь сечения Аi	Ii момент инерции	yi2*Ai
1	-2t	4t2		16t4
2	1t	8t2		8t4

3. Моменты сопротивления

;

Подбор сечения балки

Из условия прочности на растяжение

Из условия прочности на сжатие

Из полученных значениц принимаем большее, t=43,6мм.

4. Расчет замкнутой цилиндрической оболочки, работающей в условиях сложного сопротивления

Определение ВСФ. Вычислим продольную силу в одном из сечений

Изгибающий момент

Ми=F2*e=(-32)0.07=-2.24kHm

Крутящий момент

Мк=-2,8кНм.

Исследование напряженного состояния и утсановление опасной точки. Вычислим предварительное геометрические характеристики поперечного сечения оболочки:

Площадь

Осевой момент сопротивления

Полярный момент сопротивления

Из двух наиболее удаленных точек опасной будет точка 12, где нормальные напряжения от продольной силы N и изгибающего момента Ми складываются.

На гранях элемента, выделенного в окрестностях опасной точки, действующие напряжения

Нормальные, обсловлены внутренним давлением

Нормальные , вызванные продольной силой N и изгибающим моментом Ми

Касательные напряжения вызванные крутящим моментом Мк:

По найденным величинам определяем величины главных напряжений

Учитывая, что , имеем следующие величины главных напряжений

Оценка прочности конструкцийй. Пользуясь энергетической теорией прочности, вычисляем эквивалентное напряжение

Запас прочности конструкции по пределу текучести

Как видим, запас вполне достаточный, поэтому прочность конструкции обеспечена.

5.Расчет стержня на устойчивость.

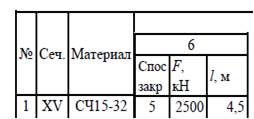
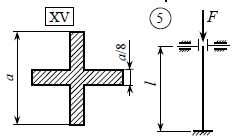
Определение геометрических характеристик

А=а*а/8+(а-а/8)*а/8=0,234а²

Минимальный момент инерции

Imin=

Минимальный радиус инерции

Вычисленные характеристики можно записать в общем виде

Здесь к1=0,234, к2=0,0711, к3=0,551, d=a – характерный размер сечения.

Искомый характерный размер сечения находится из трансцендентного уравнения:

Которое решается методом последовательных приближений.

Первое приближение. Примем , тогда

=

Тогда гибкость стержня

По таблице найдем

Расхождение

Значит характерный размер сечения, округлив по ГОСТ 6636, примем а=320мм.

Определим коэффициент запаса устойчивости

Гибкость стержня при а=320мм

, значит стержень обладает средней гибкостью. Опеределим критическую силу

=

Коэффициент запаса устойчивости

Для чугунных стержней коэффициент запаса устойчивости должен быть в диапазоне [4…7].

6.Индивидуальные задачи

6.1Сложное сопротивление : изгиб с кручением

Построив эпюры изгибающего Mx и крутящего Mz моментов, вычислим расчетные напряжения в сечениях

Wx=0.1d³ =0.1*0.02 ³=0,8*10^-6 м³

Вычислим перемещения в точке D

Для этого построим единичное состояние, приложив едеиничную силу в точке D, и посторим эпюру единичного состояния.

При этом перемещение в точке D вычислим, перемножив эпюру единичного состояния на эпюры ВСФ.

6.2Динамическое нагружение: расчеты на удар.

Определяем параметры статического нагружения:

Вычислим коэффициент динамический по формуле

Вычислим напряжение

6.3Переменные напряжения.

Параметры очага концентрации

L=2b=2*12=24мм

G=2.3/r=2.3/5=0.461/мм

По графику (рис. 3.6) находим теоретический коэффициент концентрации напряжений = 2,72. Теперь определяем множитель

=

Из графика (рис. 3.11) находим KF = 0,9

K = (K /Kd – 1/KF – 1)/K = (2,648 – 1/0,9 – 1)/1 = 1,5368.

Искомое допускаемое напряжение

[ ] = -1p /(K*[n]) = 150/(1.5368*2) = 48.799 МПа.

Исходя из допускаемого напряжения вычислим допускаемую нагрузку

[F]=[ ]*A=48.799*(12*100)=58.559kH

23