Занятие №9. Дифракция Фраунгофера.

1. Монохроматический свет падает нормально на щель ширины b=11 мкм. За щелью находится тонкая линза с фокусным расстоянием f=150 мм, в фокальной плоскости которой расположен экран. Найти длину волны света, если расстояние между симметрично расположенными минимумами третьего порядка (на экране) равно x=50 мм.

2. Белый свет падает по нормали на щель ширины b=0,10 мм. За щелью установлена линза, в фокальной плоскости которой помещен экран. Оптическая сила линзы Ф=+5,0 дптр. Определить: а) ширину a радужного канта на границе наблюдаемого на экране центрального дифракционного максимума, б) отношение ширины канта a к средней ширине <x> центрального максимума.

3. Свет с длиной волны =0,50 мкм падает на щель ширины b=10 мкм под углом ₀=30 к ее нормали. Найти угловое положение первых минимумов, расположенных по обе стороны центрального фраунгоферова максимума.

4. При нормальном падении света на дифракционную решетку угол дифракции для линии _=0,65 мкм во втором порядке равен 45. Найти угол дифракции для линии _=0,50 мкм в третьем порядке.

5. Определить длину волны монохроматического света, падающего нормально на дифракционную решетку с периодом d=2,2 мкм, если угол между направлениями на фраунгоферовы максимумы первого и второго порядков =15.

6. Свет с длиной волны =0,60 мкм падает нормально на дифракционную решетку, которая нанесена на плоской поверхности плоско-выпуклой цилиндрической стеклянной линзы с радиусом кривизны R=20 см. Период решетки d=6,0 мкм. Найти расстояние между симметрично расположенными главными максимумами первого порядка в фокальной плоскости этой линзы.

7. Свет с =589,0 нм падает нормально на дифракционную решетку с периодом d=2,5 мкм, содержащую N=10000 штрихов. Найти угловую ширину дифракционного максимума второго порядка.

Занятие №10. Разрешающая способность оптических приборов. Дифракция на пространственных структурах.

1. Свет с длиной волны  падает нормально на дифракционную решетку. Найти ее угловую дисперсию в зависимости от угла дифракции .

2. Свет, содержащий две спектральные линии с длинами волн 600,000 и 600,050 нм, падает нормально на дифракционную решетку ширины 10,0 мм. Под некоторым углом дифракции  эти линии оказались на пределе разрешения (по критерию Рэлея). Найти .

3. Свет падает нормально на дифракционную решетку ширины l=6,5 см, имеющую 200 штрихов на миллиметр. Исследуемый спектр содержит спектральную линию с =670,8 нм, которая состоит из двух компонент, отличающихся на =0,015 нм. Найти: а) в каком порядке спектра эти компоненты будут разрешены; б) наименьшую разность длин волн, которую может разрешить эта решетка в области 670 нм.

4. Для трехгранной призмы спектрографа предельная разрешающая способность  обусловлена дифракцией света от краев призмы (как от щели). При установке призмы на угол наименьшего отклонения в соответствии с критерием Рэлея

,

где b - ширина основания призмы (рис.1), dn/d - дисперсия ее вещества. Вывести эту формулу.

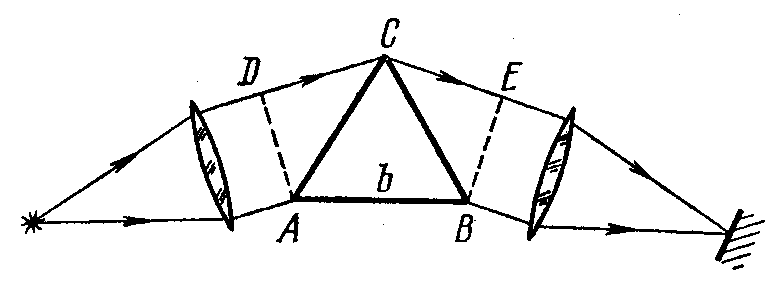
рис.1

5. Какой должна быть ширина основания трехгранной призмы с дисперсией |dn/d|=0,10 мкм^-1, чтобы она имела такую же разрешающую способность, как и дифракционная решетка из 10000 штрихов во втором порядке спектра?

6. Имеется зрительная труба с диаметром объектива D=5,0 см. Определить разрешающую способность объектива трубы и минимальное расстояние между двумя точками, находящимися на расстоянии l=3,0 км от трубы, которое она может разрешить. Считая =0,55 мкм.

7. Пучок рентгеновских лучей с длиной волны  падает под углом скольжения 60,0 на линейную цепочку из рассеивающих центров с периодом a. Найти углы скольжения, соответствующие всем дифракционным максимумам, если a.

Узкий пучок рентгеновских лучей падает под углом скольжения =60,0 на естественную грань монокристалла NaCl, плотность которого =2,16 г/см³. При зеркальном отражении от этой грани образуется максимум второго порядка. Определить длину волны излучения.