Занятие №3. Отражение и преломление света.

1. Луч света падает на плоскопараллельную стеклянную пластину толщиной d=6,0 см. Угол падения = 60. Найти величину смещения луча, прошедшего через эту пластину.

2. На краю бассейна стоит человек и наблюдает камень, лежащий на дне. Глубина бассейна h. На каком расстоянии от поверхности воды видно изображение камня, если луч зрения составляет с нормалью к поверхности воды угол ?

3. Показать что при преломлении в призме с малым преломляющим углом  луч отклоняется на угол (n - 1) независимо от угла падения, если последний также мал.

4. Луч света проходит через призму с преломляющим углом  и показателем преломления n. Пусть  - угол отклонения луча. Показать, что при симметричном ходе луча через призму: а) угол  минимален; б) связь между углами  и  определяется формулой.

5. Для некоторой стеклянной призмы угол наименьшего отклонения луча равен преломляющему углу призмы. Найти последний.

6. Трехгранная призма с преломляющим углом 60 дает угол наименьшего отклонения в воздухе 37. Какой угол наименьшего отклонения даст эта призма в воде?

7. Луч света, содержащий две монохроматические составляющие, проходит через трехгранную призму с преломляющим углом =60. Определить угол  между обеими составляющими луча после призмы, если показатели преломления для них равны 1,515 и 1,520 и призма ориентирована на угол наименьшего отклонения.

8. Вывести с помощью принципа Ферма законы отражения и преломления света на плоской границе раздела двух сред.

Занятие №4. Сферические зеркала и линзы.

1. Найти построением:

а) ход луча после отражения в вогнутом и выпуклом сферических зеркалах (рис. 1, где F- фокус, ОО - оптическая ось);

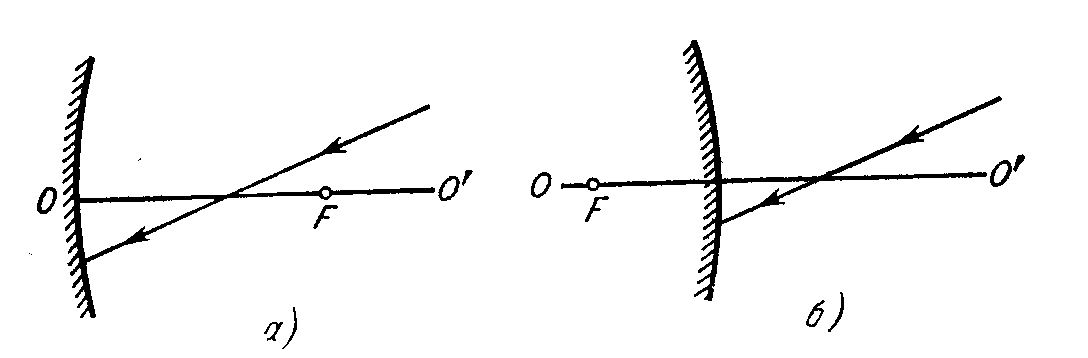
рис.1

б) положение зеркала и его фокуса для случаев, показанных на рис.2 , где Р и Р - сопряженные точки.

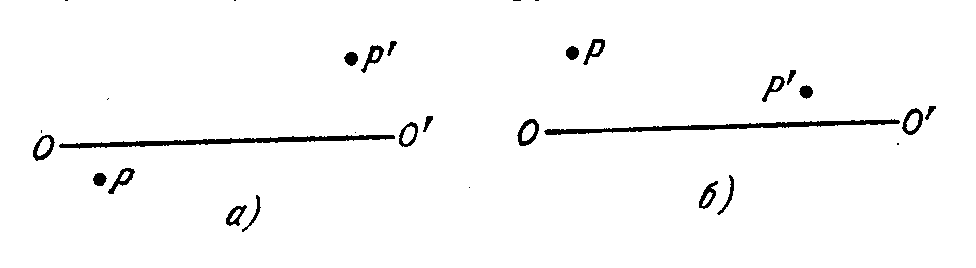
рис. 2

2. Определить фокусное расстояние вогнутого зеркала, если: а) при расстоянии между предметом и изображением l=15 см поперечное увеличение = 2,0; б) при одном положении предмета поперечное увеличение ₁=0,50, а при другом положении, смещенном относительно первого на расстояние l=5,0 см, поперечное увеличение ₂=0,25.

3. Точечный источник, сила света которого I₀=100 кд, помещен на расстоянии s=20,0 см от вершины вогнутого зеркала с фокусным расстоянием f = 25,0 см. Определить силу света в отраженном пучке, если коэффициент отражения зеркала =0,80.

4. Точечный источник расположен на расстоянии 20 см от передней поверхности стеклянной симметричной двояковыпуклой линзы. Толщина линзы 5,0 см, радиус кривизны поверхностей 5,0 см. На каком расстоянии от задней поверхности этой линзы образуется изображение источника?

5. Перед выпуклой поверхностью стеклянной выпукло-плоской линзы толщины d=9,0 см находится предмет. Изображение этого предмета образуется на плоской поверхности линзы, которая служит экраном. Определить: а) поперечное увеличение, если радиус кривизны выпуклой поверхности линзы R=2,5 см; б) освещенность изображения, если яркость предмета L=7700 кд/м² и диаметр входного отверстия выпуклой поверхности линзы D=5,0 мм; потери света пренебрежимо малы.

6. Найти оптическую силу и фокусные расстояния: а) тонкой стеклянной линзы в жидкости с показателем преломления n₀=1,7, если ее оптическая сила в воздухе Ф₀=5,0 дптр; б) тонкой симметричной двояковыпуклой стеклянной линзы, с одной стороны которой находится воздух, а с другой - вода, если оптическая сила этой линзы в воздухе Ф₀=+10 дптр.

7. Найти построением: а) ход луча за собирающей и рассеивающей тонкими линзами (рис.3, где ОО - оптическая ось, F и F - передний и задний фокусы); б) положение тонкой линзы и ее фокусов, если известно положение оптической оси ОО и положение пары сопряженных точек PP (см. рис.2); среды по обе стороны линз одинаковы; в) ход луча 2 за собирающей и рассеивающей тонкими линзами (рис.4), если известно положение линзы и ее оптической оси ОО и хода луча 1; среды по обе стороны линз одинаковы.

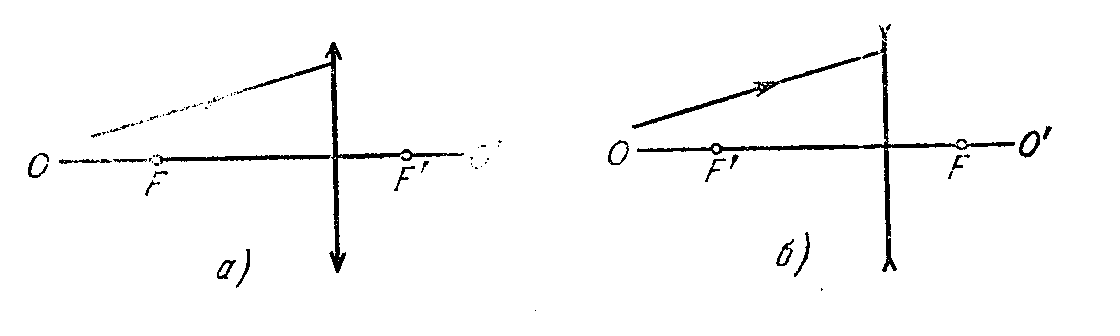
рис.3

рис.4

8. Тонкая собирающая линза с фокусным расстоянием f = 25 см проецирует изображение предмета на экран, отстоящий от линзы на расстояние l=5,0 м. Экран придвинули к линзе на l=18 см. На сколько следует переместить предмет, чтобы опять получить четкое изображение его на экране?

9. Источник света находится на расстоянии l=90 см от экрана. Тонкая собирающая линза, помещенная между источником света и экраном, дает четкое изображение источника при двух положениях. Определить фокусное расстояние линзы, если: а) расстояние между обоими положениями линзы l=30 см; б) поперечные размеры изображения при одном положении линзы в =4,0 раза больше, чем при другом.

10. Между предметом и экраном, положения которых неизменны, помещают тонкую собирающую линзу. Перемещением линзы находят два положения, при которых на экране образуется четкое изображение предмета. Найти поперечный размер предмета, если при одном положении линзы размер изображения h=2,0 мм, а при другом h=4,5 мм.

11. Вывести с помощью принципа Ферма формулу преломления параксиальных лучей на сферической поверхности радиуса R, разделяющей среды с показателями преломления n и n.