Занятие №1. Упругие волны. Электромагнитные волны.

1. Два когерентных колебания одинакового направления характеризуются комплексными амплитудам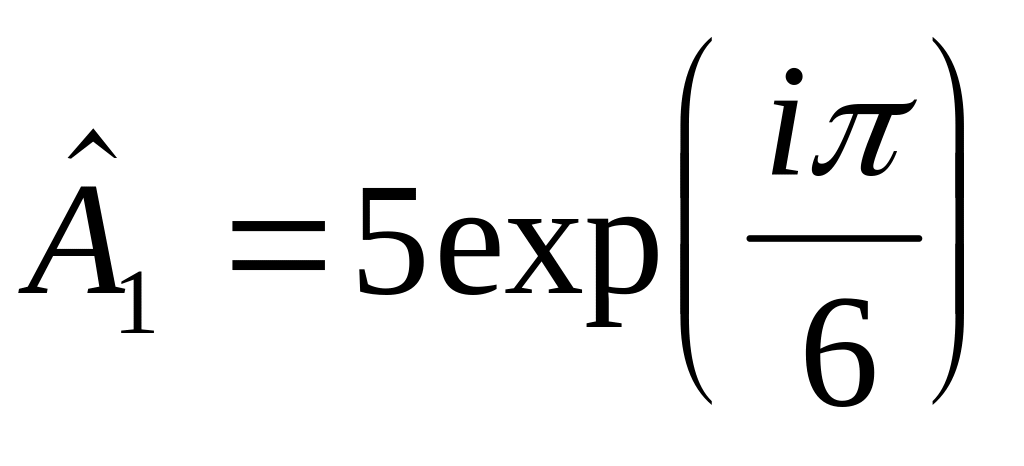и и . Найти комплексную амплитуду результирующего колебания.

2. Плоская продольная упругая волна распространяется в положительном направлении оси x в среде с плотностью =4,0 г/см³ и модулем Юнга E=100 ГПа. Найти проекцию скорости u_x частиц среды в точках, где относительная деформация среды =0,010.

3. В однородной среде распространяется плоская упругая волна вида 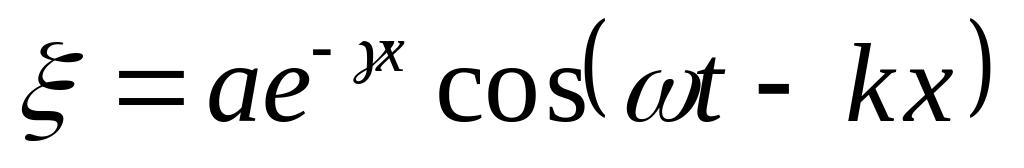, где a, ,  и k - постоянные. Найти разность фаз колебаний в точках, где амплитуды смещения частиц среды отличаются друг от друга на =1,0%, если =0,42 м^-1 и длина волны =50 см.

4. Точечный изотропный источник испускает звуковые колебания с частотой =1,45 кГц. На расстоянии r₀=5,0 м от источника амплитуда смещения частиц среды a₀=50 мкм, а в точке А, находящейся на расстоянии r=10,0 м от источника, амплитуда смещения в =3,0 раза меньше a₀. Найти: а) коэффициент затухания волны ; б) амплитуду колебаний скорости частиц среды в точке А.*

1. Изотропный точечный источник, звуковая мощность которого P=0,10 Вт, находится в центре круглого полого цилиндра радиуса R=1,0 м и высоты h=2,0 м. Полагая, что стенки цилиндра полностью поглощают звук, найти средний поток энергии, падающий на боковую поверхность цилиндра.

5. В упругой среде плотности  бежит вдоль оси x волна . Написать выражение для вектора Умова j (вектора плотности потока энергии).

6. По трубе сечения S бежит плоская затухающая волна амплитуда волны убывает по закону exp (-x). В сечении с координатой x₁ среднее (по времени) значение модуля вектора Умова равно j₁. Какое количество энергии W поглощается за время t, много большее периода волны, в объеме, заключенном между сечениями с координатами x₁ и x₂?

7. В однородной и изотропной среде с =3,00 и =1,00 распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны E_m=10,0 В/м. Найти: а) амплитуду напряженности магнитного поля волны H_m, б) фазовую скорость волны v.

1. В некоторой среде распространяется электромагнитная волна частоты . Диэлектрическая проницаемость среды при частоте  равна =2,00, магнитная проницаемость практически равна единице. Найти вектор Пойнтинга S в той точке, в которой электрический вектор изменяется по закону E = 10,0 cos (t+)e_z (В/м). Вектор H колеблется вдоль оси x.

2. Плоский конденсатор с круглыми пластинами заряжается постоянным током в течение времени  до напряжения U. Зазор между пластинами равен d. Проведя между пластинами коаксиальную с ними воображаемую цилиндрическую поверхность, радиус которой r много меньше радиуса пластин, определить: а) модуль и направление вектора Пойнтинга в точках поверхности, б) количество энергии W, протекающей через поверхность за время . Сравнить W с энергией электрического поля, содержащейся в ограниченном поверхностью объеме V после окончания процесса зарядки.

3. Сила тока в очень длинном соленоиде увеличивается равномерно от нуля до I в течение времени . Число витков соленоида на единицу длины равно n. Проведя внутри соленоида в средней его части коаксиальную с ним воображаемую замкнутую поверхность длины l и радиуса r, определить: а) модуль и направление вектора Пойнтинга в точках поверхности, б) количество энергии W, протекающей через поверхность за время . Сравнить W с энергией магнитного поля, содержащейся в ограниченном поверхностью объеме Vпосле установления силы тока I.