Міністерство освіти і науки України

Тернопільський національний економічний університет

ІНСТРУКТИВНО-МЕТОДИЧНІ

МАТЕРІАЛИ

до практичних занять, індивідуальних

та самостійних робіт

з економетрії

(для студентів усіх форм навчання)

студента групи _________

________________________

_________________________________

Тернопіль-2013

Тема 1. Однофакторні лінійні економетричні моделі

Заняття 1, 2

Вибірка змінних та задається табл.1:

Таблиця 1

	3.4	5.5	7.2	8.3	7.4	9.5	11.4	10.5	10.3	14.5
	3.1	3.3	3.7	3.1	3.9	6.3	6.1	6.5	7.8	8.9

Необхідно:

1. Провести специфікацію моделі.

2. Розрахувати оцінки а₀ та а₁ методом:

• МНК (за системою нормальних рівнянь);

• МНК (через відхилення від середніх).

3. Дати геометричну інтерпретацію оціночних рівнянь.

4. Обчислити загальну, пояснену і непояснену дисперсії.

5. Інтервал довір’я (р=0.9) рівняння економетричної моделі.

6. Коефіцієнт детермінації і кореляції.

7. Інтервал довір’я (р=0.9) параметрів та .

8. Перевірити нульову гіпотезу щодо коефіцієнту кореляції r (р=0.95). Перевірити нульову гіпотезу щодо кутового коефіцієнту а₁ (р=0.95).

9. Перевірити адекватність прийнятої економетричної моделі експериментальним даним (р=0.95).

Хід роботи.

1) Специфікацію моделі здійснюємо з допомогою діаграми розсіювання. В прямокутній декартовій системі координат xOy будуємо точки {x_i, y_i} (i = ), координати яких визначаються табл. 1 (див. рис. 1).

Рис. 1

Переконавшись з графіку, що залежність між фактором і показником лінійна, знаходимо оціночне рівняння у вигляді:

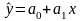
2) Оцінки параметрів та 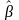обчислюємо з системи нормальних рівнянь методу найменших квадратів

де n – об’єм вибірки .

Будуємо розрахункову таблицю Табл. 2

N	i	i	i i	i2
1	3,10	3,40	10,54	9,61
2	3,30	5,50	18,15	10,89
3	3,70	7,20	26,64	13,69
4	3,10	8,30	25,73	9,61
5	3,90	7,40	28,86	15,21
6	6,30	9,50	59,85	39,69
7	6,10	11,40	69,54	37,21
8	6,50	10,50	68,25	42,25
9	7,80	10,30	80,34	60,84
10	8,90	14,50	129,05	79,21
SS	52,7	88.0	516.95	318,21

Система рівнянь в числах набере вигляду

Ці ж оцінки знайдемо не розв’язуючи системи нормальних рівнянь. Згідно МНК через відхилення від середніх значень

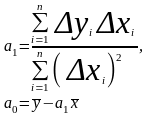де

Будуємо розрахункову таблицю Табл. 3

N
1	3,10	3,40			-5,40	-2,17	4,71	11,72
2	3,30	5,50			-3,30	-1,97	3,88	6,50
3	3,70	7,20			-1,60	-1,57	2,46	2,51
4	3,10	8,30			-0,50	-2,17	4,71	1,09
5	3,90	7,40	5,27	8.8	-1,40	-1,37	1,88	1,92
6	6,30	9,50			0,70	1,03	1,06	0,72
7	6,10	11,40			2,60	0,83	0,69	2,16
8	6,50	10,50			1,70	1,23	1,51	2,09
9	7,80	10,30			1,50	2,53	6,40	3,80
10	8,90	14,50			5,70	3,63	13,18	20,69
SS	52,7	88.0			0	0	40.48	53.19

Отже, оціночне рівняння має вигляд

4) Знаходимо загальну, пояснену і непояснену дисперсії по формулах

; .

Необхідні обчислення приведені в таблиці: Табл 4

N				2				( - )2	( - )2
1	3,10	3,40	-5,40	29,16	5,95			8,13	6,50
2	3,30	5,50	-3,30	10,89	6,21			6,70	0,51
3	3,70	7,20	-1,60	2,56	6,74			4,26	0,21
4	3,10	8,30	-0,50	0,25	5,95			8,13	5,53
5	3,90	7,40	-1,40	1,96	7,00			3,24	0,16
6	6,30	9,50	0,70	0,49	10,15			1,83	0,43
7	6,10	11,40	2,60	6,76	9,89			1,19	2,28
8	6,50	10,50	1,70	2,89	10,42			2,61	0,01
9	7,80	10,30	1,50	2,25	12,12			11,05	3,33
10	8,90	14,50	5,70	32,49	13,57			22,75	0,87
SS	52.7	88	0	89.7		88.0	69.89		19.81

Дисперсії =89.7/10=8.97, = 69.89/10=6.99, = 19.81/10=1.98

5) Граничну похибку оцінки за рівнянням економетричної моделі знаходимо по формулі

де - імовірносний коефіцієнт, який при заданих рівнях імовірності р знаходиться за таблицями нормального розподілу. При цьому розв’язуємо рівняння 2Ф(t_p)=p, де Ф(t) – функція Лапласа. Для р =0.9 ( =1.65 ). Одержуємо =1,83. Довірчий інтервал знаходимо з нерівності

- 1,83 + 1,83

- 1,83 + 1,83

+ 0.045

Для наочного уявлення одержаних розрахунків будуємо графіки : фактичних даних , оціночного рівняння , довірчого інтервалу.

Рисунок 2

6) Знайдемо значення коефіцієнта детермінації за формулою

=

і коефіцієнта кореляції за формулою

.

Так як r=0,98, то це вказує, що оціночна пряма пояснює 98% загальної дисперсії.

Дисперсія зумовлена випадковою складовою (невраховані фактори, помилки виміру, суб’єктивний чинник) складає лише 2%. Знак коефіцієнта кореляції повинен співпадати з знаком а₁.

7) Переходимо до знаходження довірчих інтервалів для параметрів та . Вони знаходяться аналогічно довірчим інтервалам оцінки за рівнянням економетричної моделі. Спочатку знаходимо граничні похибки оцінок за формулою

, ,

де , - середньоквадратичні відхилення оцінок та , які визначаються за формулами

, = .

, = .

Обчислюємо = , = ;

,

Отже,

довірчий інтервал для параметра

- £Ј aa₀ £Ј +

29,46 - 1,38£Ј aa₀ £Ј 29,46 + 1,38

28,08 £Ј aa₀ £Ј 30,84.

Довірчий інтервал для параметра

- £Ј aa₁ £Ј +

-0,74 - 0,07 aa₁ -0,74 + 0,07

-0,81  aa₁  -0,67.

8) Коефіцієнт кореляції r знайдено на основі вибіркових даних і він є випадковою величиною. Зробимо перевірку нульової гіпотези. Згідно з нею коефіцієнт кореляції в генеральній сукупності дорівнює нулю (відсутній кореляційний зв’язок між Y і X в генеральній сукупності) і необхідно дослідити сумісність коефіцієнта кореляції із нашої вибірки (r ) з даною гіпотезою. Нульова гіпотеза Н₀: r_ген = 0, альтернативна гіпотеза Н₁: r_ген ¹№ 0. Для вибірки обчислюється статистика

яка має розподіл Стьюдента з k=n-2 ступенями вільності. Для заданої ймовірності р і k ступенів вільності знаходимо табличне значення - статистики. Якщо то із заданою надійністю р гіпотезу Н₀ слід відкинути і прийняти альтернативну гіпотезу Н₁ про існування залежності між цими випадковими величинами. = . Табличне значення =2.306 для надійності р=0.95. Емпіричне значення t більше критичного, тому нульова гіпотеза відхиляється. В 95% вибірок з генеральної сукупності коефіцієнт кореляції не дорівнює нулю.

Перевіримо нульову гіпотезу стосовно оцінки а₁. Знаходимо емпіричне значення відношення для перевірки нульової гіпотези за формулою: . = 18,5.

Табличне значення =2.306 для надійності р=0.95. Емпіричне значення t більше критичного, тому нульова гіпотеза відхиляється. Кутовий коефіцієнт а₁ розрахований по вибірці вважається статистично значущим з імовірністю 0,95.

9) Для визначення адекватності прийнятої економетричної моделі експериментальним даним скористаємося F - критерієм Фішера. Розрахункове значення критерію (m-кількість факторів ).

= =156,79.

Табличне значення критерію для ймовірності р =0,95 і числа ступенів вільності k₁= m=1, k₂=n-m-1=10-2=8 дорівнює 5,32 (див. висн.).