§ 94. Прямоугольные координаты, отнесенные к осям меридианного эллипса

В теоретических выводах нередко возникает необходимость пользо­ваться системой прямоугольных координат, отнесенных к осям мериди­анного эллипса PQP₁Q₁ проходящего через точку М (рис. 131). В такой системе центр эллипсоида О принимают за начало координат, экваториальную ось QQ₁ — за ось абсцисс (х) и полярную ось PP₁ — за ось ординат (у). Положение меридиана относительно начального PEP₁ E ₁(рис. 130) определяют, как видно, гео­дезической долготой L.

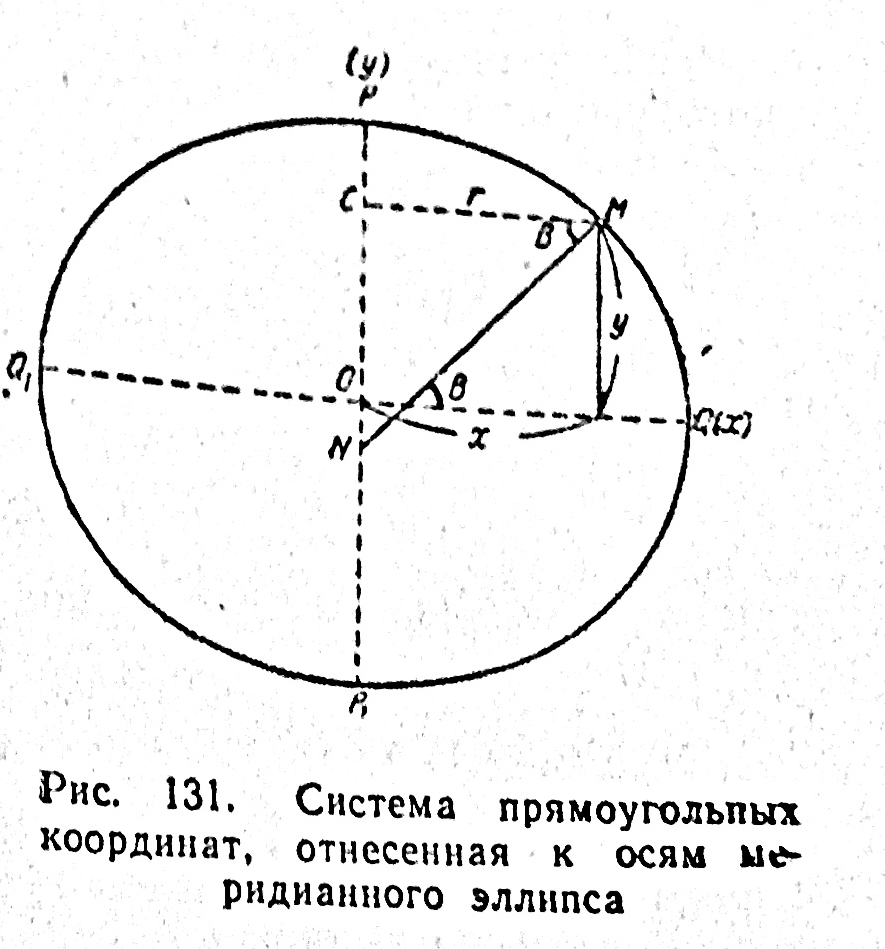
Но вместо геодезической широты D в этом случае берут прямоугольные координаты x и y. Связь их с геодезической широтой точки М устанавливается следующими формулами. Как известно, уравнение эллипса в канонической форме имеет вид

Известно также, что

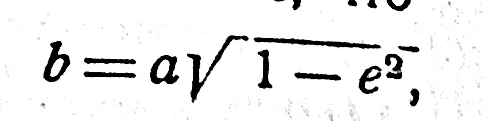
где величина е — эксцентриситет эллипса. Следовательно, урав­нение (172) можно написать еще так:

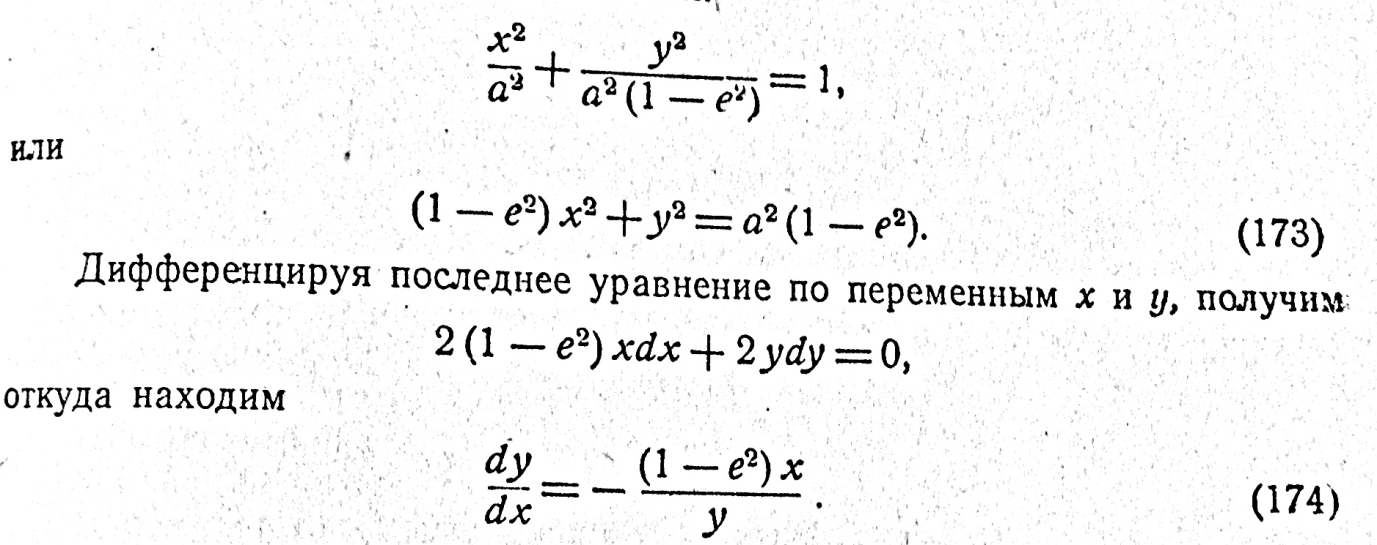
Но из математического анализа известно, что первая производная 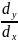равна отрицательному , значению котангенса угла В, образован­ного нормалью MN (рис. 131) с положительным направлением оса абсцисс OQ, т.е.:

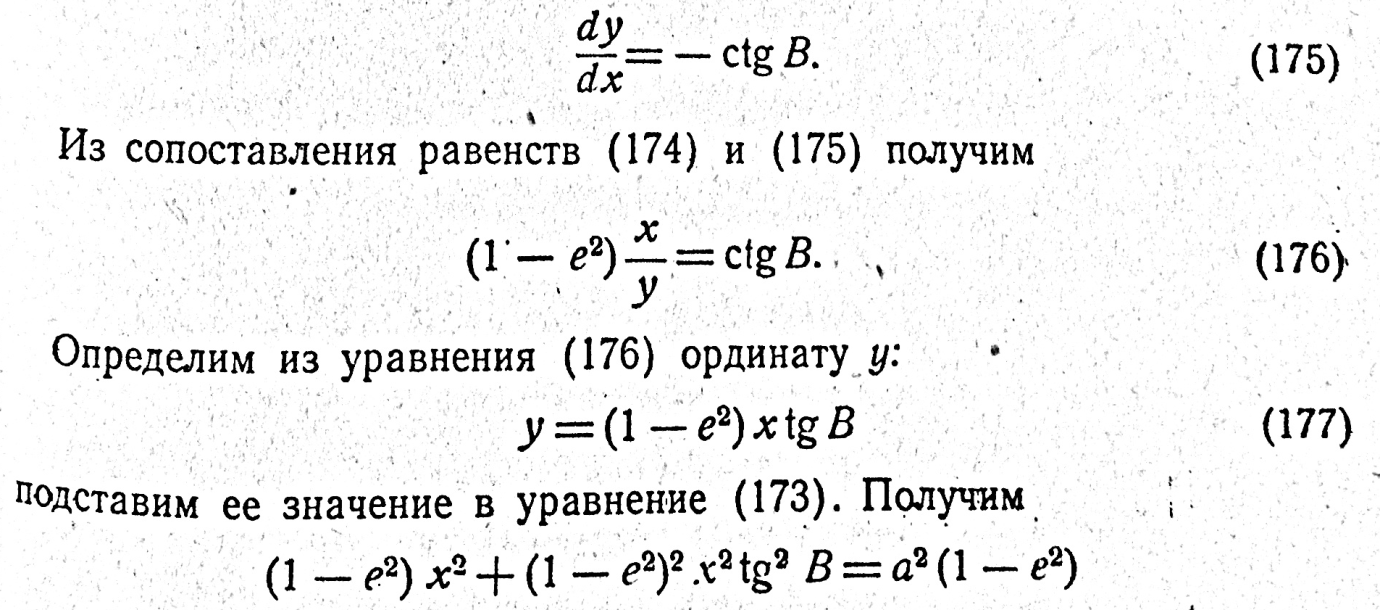
Уравнения (178) и (179) и служат для связи геодезической широты В с прямоугольными координатами х и у, отнесенными к осям меридиан­ного эллипса. Как видно из рис. 131, уравнение (178) является одновре­менно формулой для определения радиуса параллели, проходящей через данную точку М, т. е.

§ 95. Радиусы кривизны

Через данную точку на поверхности эллипсоида можно провести бесконечное множество нормальных сечений, которые в разных направ­лениях будут иметь разную кривизну. Но для вычисления различных геодезических величин, связанных с кривизной поверхности эллипсоида, выделяются только два нор­мальных сечений, кривизну которых необхо­димо знать. Это главные нормальные сече­ния: меридиан и сечение первого вертикала. Кривизна их определяется радиусами кривизны, которые, по аналогии с соответствую­щими, нормальными сечениями носят назва­ние главных радиусов кривизны и обозначаются: радиус кривизны меридиа­на через М, а радиус к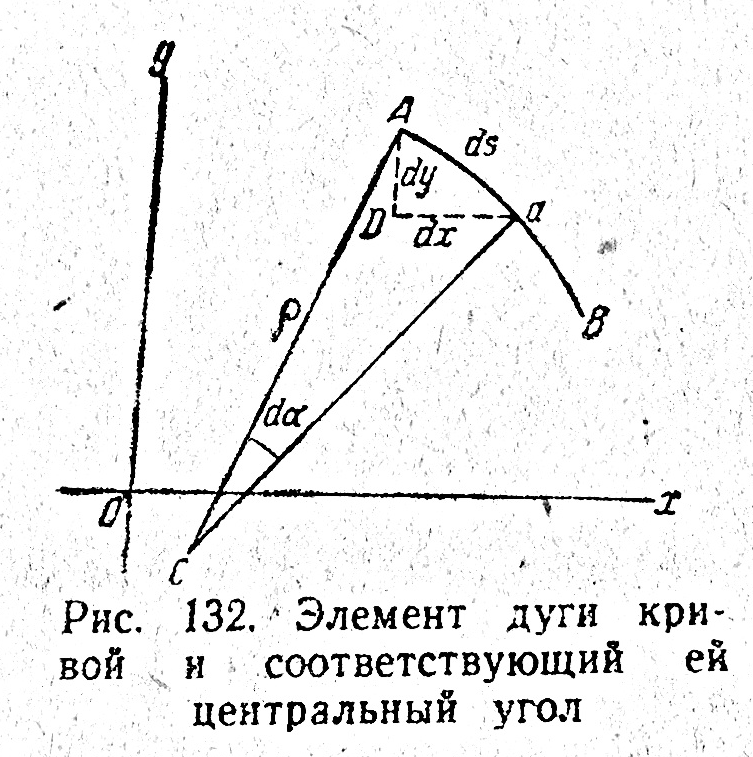 ривизны первого вертикала — через N.

Определим радиус кривизны мери­диана М.

Из математики известна, что кривизна любой плоской кривой АВ (рис. 132) определяется в общем виде формулой

Принимая кривую АВ за дугу меридиана, а элементы ds, р и dа кривой — соответственно за элементы ds, М и dB меридиана, формулу (181) перепишем так:

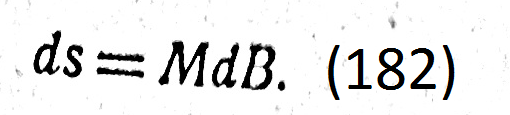
Если через точки A и а данной фигуры провести параллельно осям плоских координат прямые AD = dx и DA = dy, то из бесконечно малого треугольника AaD будем иметь

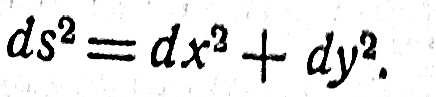
Отсюда пишем

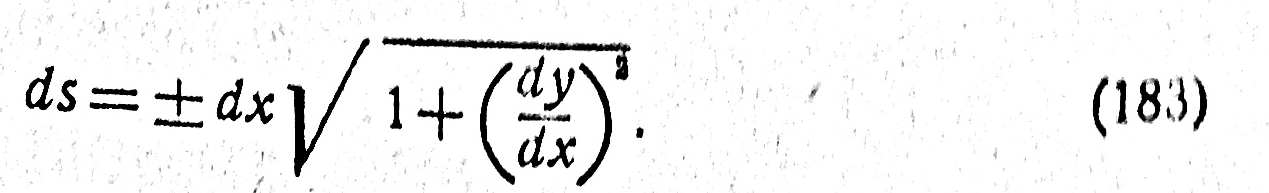
Учитывая (175), (182), найдем после небольших преобразований

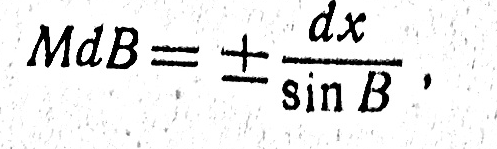
Откуда

\

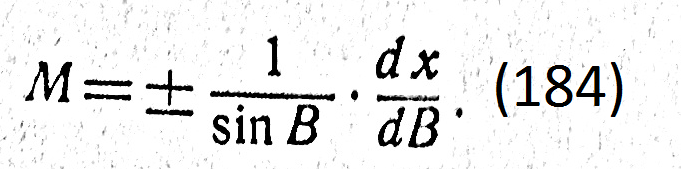
Дифференцируя выражение (178) по В, получим

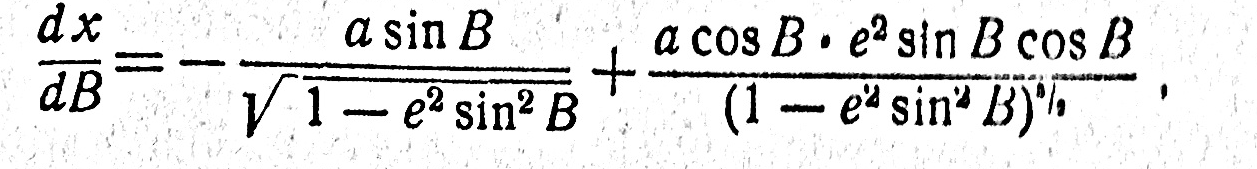
Или

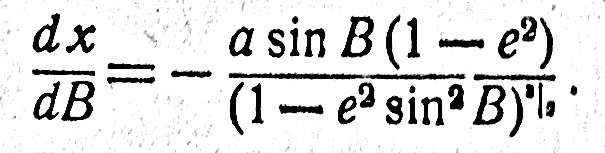
Подставим теперь значение этой производной в формулу (184). Так как величина М существенно положительная, то для радиуса кривизны меридиана получим окончательно

Формулу радиуса кривизны первого вертикала приведем без вывода

Сопоставляя (186) и (180), замечаем, что

Из формул (185) и (186) видно, что радиусы кривизны М и N главных нормальных сечений увеличиваются с возрастанием широты В. Следовательно, кривизна этих сечений уменьшается с перемещением от экватора к полюсам.

Указанными формулами определяется также, что радиус кривизны меридиана М является наименьшим, а радиус кривизны первого вертикала N — наибольшим в данной точке. На полюсах М =N.

При вычислении некоторых геодезических величин поверхность эл­липсоида заменяют поверхностью шара. В этом случае радиус шара берут равным среднему арифметическому из радиусов кри­визны всех возможных нормальных сечений в данной точке. В оконча­тельном виде средний радиус кривизны равен

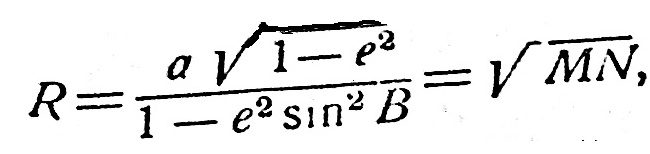
т. е. среднему геометрическому из радиусов кривизны глав­ных нормальных сечений.

Р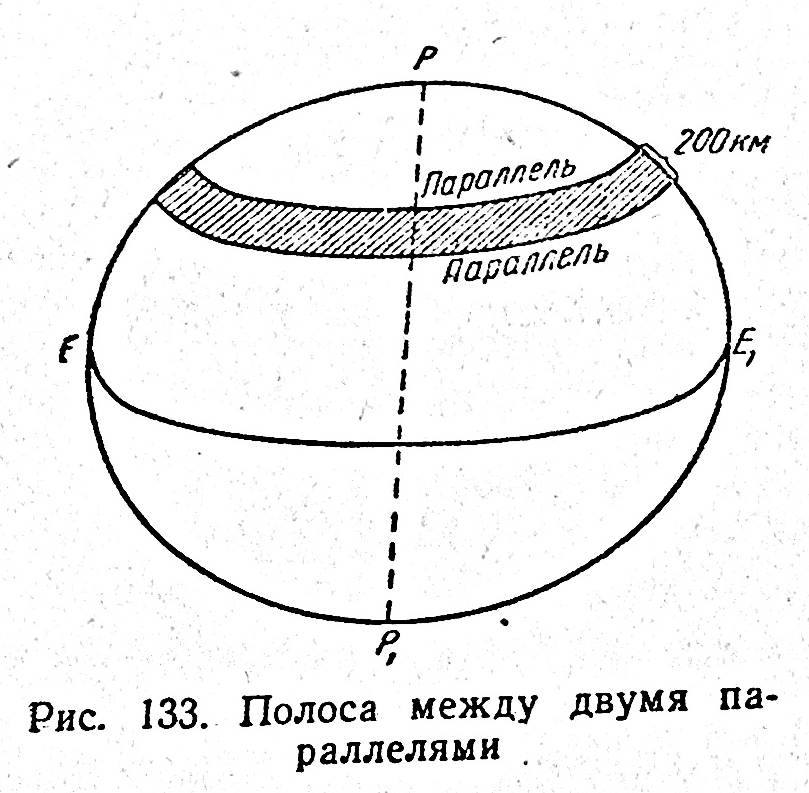 адиусы кривизны М и N — основные элементы сфероидической геодезии, без которых вычисления многих геодезических величин на по­верхности эллипсоида невозможны. В частности, радиус кривизны мери­диана М необходим для вычисления длин дуг меридиана и разностей ши­рот, а радиус кривизны первого вер­тикала N — для вычисления длин дуг параллелей, разностей долгот и разно­стей азимутов (сближений меридиа­нов).

Средний радиус кривизны R ис­пользуется в геодезии для вычисления сферических избытков треугольников, а также при замене некоторых частей поверхности эллипсоида поверхностью шара. Как показывают расчеты, такая замена практически не отражается на точности геодезических работ в преде­лах двухградусной (по широте) полосы, т.е. в пределах полосы шириной (между двумя параллелями) до 200 км (рис. 133).

Для величин М, N и R имеются специальные таблицы*, в которых численные значения их даются в форме выражений

Здесь ρ" — число секунд в радиане, равное 206 265",806; как изве­стно, число это вводится в вычисления для перевода угловых величин из градусной меры в аналитическую и наоборот.