
- •Перевіряємо готовність до вивчення розділу
- •Вхідний тест
- •1. Складаємо опорний конспект
- •2. Контрольні питання
- •3. Задачі і вправи
- •1. Складаємо опорний конспект
- •2. Контрольні питання
- •3. Задачі і вправи
- •1. Складаємо опорний конспект
- •2. Контрольні питання
- •3. Задачі і вправи
- •1. Складаємо опорний конспект
- •2. Контрольні питання
- •3. Задачі і вправи
- •1. Складаємо опорний конспект
- •2. Контрольні питання
- •3. Задачі і вправи
- •1. Складаємо опорний конспект
- •2. Контрольні питання
- •3. Задачі і вправи
- •Індивідуальне завдання 2
- •Варіанти для виконання індивідуального завдання 2
- •Приклад виконання варіанта індивідуального завдання Дослідіть поверхню
- •Демонстраційні варіанти модульної контрольної роботи до розділу «Теорія поверхонь»
- •Демонстраційний варіант екзаменаційної роботи
- •Зведення поверхонь
- •Список рекомендованої літератури
3. Задачі і вправи
Задачі та вправи
для самостійної роботи
та роботи в аудиторії
Знайдіть другу квадратичну форму поверхні:
1)
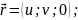
2)
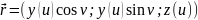 .
.
Приклад. .
Розв’язання.
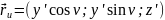
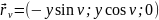
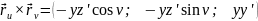
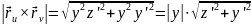
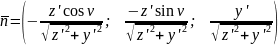
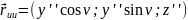



Відповідь:
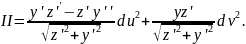
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Знайдіть нормальну кривину:
а) площини в довільному напрямку дотичної площини;
б) сфери в довільному напрямку дотичної площини;
в) циліндра у напрямку дотичної площини, паралельнім твірній;
г) циліндра у напрямку дотичної площини, перпендикулярнім твірній;
д) циліндра в довільному напрямку дотичної площини.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Доведіть, що при будь-якому виборі криволінійних координат на площині друга квадратична форма тотожно дорівнює нулю.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Доведіть, що поверхня є частиною площини, якщо її друга квадратична форма дорівнює нулю.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Доведіть, що індикатриса Дюпена є або еліпсом, або парою паралельних прямих, або парою спряжених гіпербол.
Приклад.
Розв’язання.
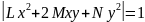 – рівняння
індикатриси Дюпена, або
– рівняння
індикатриси Дюпена, або


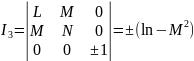
І центральні криві:
а)
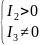 еліптичний тип;
еліптичний тип;
б)
 гіперболи;
гіперболи;
в)
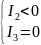 дві прямі, що перетинаються. У нашому
випадку не може бути;
дві прямі, що перетинаються. У нашому
випадку не може бути;
г)

 .
Не може бути.
.
Не може бути.
д)

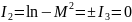 .
.
Отже, наша крива може бути або еліпсом, або парою паралельних прямих, або парою спряжених гіпербол.
Знайдіть головні кривини: а) площини; б) сфери; в) циліндра.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доведіть, що якщо в точці поверхні існує рівно два головних напрямків, то вони перпендикулярні.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знайдіть головні кривини поверхні:
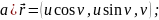
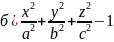 =0.
=0.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знайдіть гауссову та ейлерову кривини: а) площини; б) циліндра; в) сфери.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. Доведіть, що для поверхні має місце формула
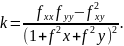
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. Знайдіть головні напрямки та головні кривини прямого гелікоїда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12.
Обчисліть
головні кривини поверхні
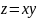 у точці
у точці
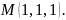
Приклад.
Розв’язання. Параметризуємо поверхню
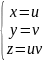
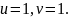
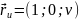 ;
;


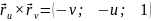
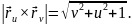

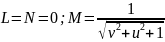
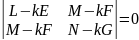 – рівняння
для знаходження головних кривин.
– рівняння
для знаходження головних кривин.

У
точці


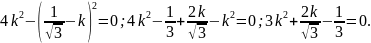
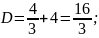
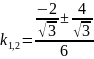 ;
;

 .
.
13. Обчисліть головні кривини поверхні
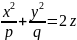
у
точці
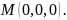
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14. Знайдіть повну та середню кривини прямого гелікоїда На яких лініях повна кривина стала?
Приклад.
Розв’язання.
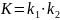 – повна кривина поверхні;
– повна кривина поверхні;
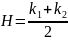 – середня
кривина поверхні,
де
– середня
кривина поверхні,
де

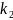 – головні
кривини.
– головні
кривини.
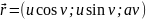




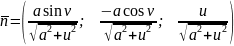
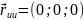

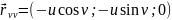

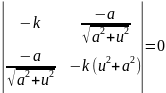
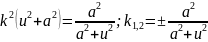 – головні
кривини.
– головні
кривини.
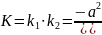 Мінімальна
поверхня.
Мінімальна
поверхня.
15.
Знайдіть
кривини нормальних перерізів поверхні
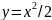
а) у довільній точці;
б)
у точках ліній, які одержуються при
перерізах поверхні площинами,
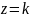 ;
у напрямках,
що
ідуть по
дотичним
до
цих
ліній;
;
у напрямках,
що
ідуть по
дотичним
до
цих
ліній;
в)
у точці
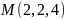 в напрямку дотичної до лінії
в напрямку дотичної до лінії

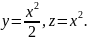
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.
На
поверхні
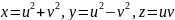 дана точка
дана точка
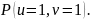
а)
обчисліть
головні кривини поверхні у точці
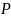 .
.
б)
знайдіть
рівняння дотичних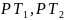 до головних нормальних перерізів у
вказаній точці.
до головних нормальних перерізів у
вказаній точці.
в)
обчисліть кривину нормального перерізу
у точці
,
який проходить через дотичну до лінії
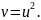
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. Дана поверхня
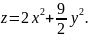
а) знайдіть в початку координат рівняння індикатриси Дюпена.
б) обчисліть в початку координат радіус кривини нормального перерізу, дотична до якого складає кут 45 з віссю Ох.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18*.
Знайдіть повну та середню кривину
поверхні обертання
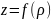 ,
де
,
де
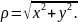
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Покажіть, що координатні лінії поверхні
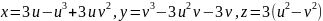
є лініями кривини.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дослідіть характер точок на наступних поверхнях другого порядку:
Еліпсоїд;
Однопорожнинний гіперболоїд;
Двопорожнинний гіперболоїд;
Еліптичний параболоїд;
Гіперболічний параболоїд;
Еліптичний циліндр;
Параболічний циліндр;
Гіперболічний циліндр;
Конус без вершини.
Приклад. Еліпсоїд обертання
Розв’язання. Знайдемо другу квадратичну форму поверхні.
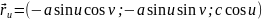
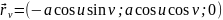

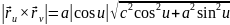
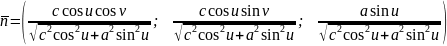
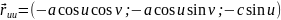
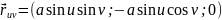
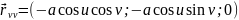
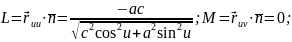
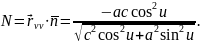
Визначимо
знак виразу
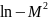 .
.
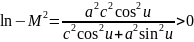 для
будь-яких
для
будь-яких
Усі точки на еліпсоїді обертання еліптичного типу.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знайдіть лінії кривини наступних поверхонь:
Довільної циліндричної поверхні;
Довільної конічної поверхні;
Довільної поверхні обертання;
Поверхні
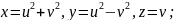
Довільної розгорнутої поверхні;
Прямого гелікоїда;
Еліптичного параболоїда.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАНЯТТЯ VI. КЛАСИФІКАЦІЯ ПОВЕРХОНЬ
