Пример реализации математической модели в системе matlab

Программа расчета переходных процессов в схеме, приведенной на рис.3, при использовании метода бегущих волн имеет вид:

% Исходные данные

tr=40e-6; - время расчета переходного процесса

h=0.1e-6; - шаг расчета

L1=1500;L2=600; - длина ВЛ и КЛ

v1=300.e6;v2=150.e6; - скорости распр. волн по ВЛ и КЛ

Z1=400;Z2=40; - волновые сопротивления ВЛ и КЛ

C=2e-9; - входная емкость трансформатора

U0=1; - амплитуда воздействующей волны

ti=2e-6; - длительность срезанного импульса

U3k=0; - начальное значение U₃(t)

nt=tr/h; - количество циклов по времени

% Начальные значения массивов напряжений и времени

UM1=0;UM2=0;UM3=0;tm=0;

% Формирование размерности для массивов волн

N1=round(1+L1/v1/h);

N2=round(1+L2/v2/h);

% Формирование начальных (нулевых) массивов волн

V12=zeros(1,N1);

V21=zeros(1,N1);

V23=zeros(1,N2);

V32=zeros(1,N2);

% Расчет волнового процесса (цикл по времени)

for k=1:nt

t=k*h;

% if(t<=ti)

% e=2*U0-2*U0*(ti-t)/ti;

% else - срезанный импульс

% e=0;

% end

e=2*U0; - прямоугольный импульс

% Сдвиг волн на шаге расчета

for i=N1:-1:2

V12(i)=V12(i-1);

V21(i)=V21(i-1);

end

for i=N2:-1:2

V23(i)=V23(i-1);

V32(i)=V32(i-1);

end

% Вычисление значений напряжения в узлах

U1=(V21(N1)+e)/2;

U2=(V12(N1)*Z2+V32(N2)*Z1)/(Z1+Z2);

U3=(U3k+h*(V23(N2)+V23(N2-1)-U3k)/2/Z2/C)/(1+h/2/Z2/C);

U3k=U3;

% Формирование массивов напряжений и времени

UM1=[UM1 U1];

UM2=[UM2 U2];

UM3=[UM3 U3];

tm=[tm t*1.e6];

% Вычисление отраженных (падающих) волн

V12(1)=2*U1-V21(N1);

V21(1)=2*U2-V12(N1);

V23(1)=2*U2-V32(N2);

V32(1)=2*U3-V23(N2);

end

s ubplot(311),plot(tm,UM1,'blue'),grid;

title('Расчетные кривые изменения u(t) в узлах')

ylabel('u1(t)')

subplot(312),plot(tm,UM2,'blue'),grid; - вывод графиков u_i(t)

ylabel('u2(t)')

subplot(313),plot(tm,UM3,'blue'),grid;

xlabel('t, мкс')

ylabel('u3(t)')

Для выяснения особенностей протекания переходных процессов в исследуемой схеме рассмотрено воздействие двух видов грозовых волн:

• по ВЛ набегает срезанная волна, образовавшаяся при перекрытии линейной изоляции воздушной линии (вариант №1 табл.П 4),

• по ВЛ набегает прямоугольная волна бесконечной длительности, имитирующая в первом приближении полную волну с крутым фронтом (вариант №7 табл.П.4 ).

На рис.4 и 5 приведены расчетные кривые изменения напряжения в узлах исследуемой схемы при воздействии импульса напряжения различной длительности. Из приведенных рисунков видно, что характер изменения напряжения в конкретных узлах схемы зависит как от формы воздействующего импульса напряжения, так и от параметров схемы, в частности, от соотношения волновых сопротивлений линий в месте их сопряжения и времени пробега волн по участкам линий.

Анализ приведенных на рис.4 расчетных осциллограмм показывает, что при воздействии на схему срезанной волны напряжения (импульса с длительностью _и= 2 мкс) форма изменения напряжения в исследуемых узлах повторяет форму воздействующего импульса напряжения, а амплитуда определяется коэффициентами преломления в соответствующих узлах. Последнее связано с отсутствием наложения преломленных и отраженных волн в любой точке схемы с распределенными параметрами. В рассматриваемом случае очень легко проверить работоспособность разработанной математической модели и правильность ее реализации на ПЭВМ.

Например, в первом узле второй импульс напряжения появляется через время t=2₁₂=2l₁/₁=21500/300=10мкс с отрицательной амплитудой, определяемой коэффициентом отражения в узле ₂₁= (Z_В2 –Z_В1)/ (Z_В2 +Z_В1) = (40 – 400)/(40 +400) = – 0,82.

Во втором узле через время, равное ₁₂ = l₁/₁=1500/300 = 5мкс , появляется импульс напряжения с амплитудой, определяемой коэффициентом преломления в месте сопряжения ВЛ и КЛ ₁₂=2Z₂/(Z₂ +Z₁)= 0,18.

В третьем узле схемы напряжение на трансформаторе (емкости) появляется через время t = ₁₂+₂₃ = 1500/300 + 600/150 = 9 мкс с практически удвоенной амплитудой по отношению к величине напряжения в узле 2. В дальнейшем появление импульсов напряжения в схеме с убывающими амплитудами обусловлено преломлением и отражением волн в кабельной вставке, нагруженной на входную емкость трансформатора.

Иной характер волнового процесса будет иметь место при воздействии на исследуемую схему импульса напряжения бесконечной длительности (рис.5,а). В этом случае за счет многократного отражения и наложения волн емкость кабельной вставки заряжается до существенно большего значения напряжения. Если же заменить кабельную вставку (волновое сопротивление которой на порядок меньше волнового сопротивления ВЛ) на участок воздушной линии (Z_В2=Z_В1), то преломленных и отраженных волн в узле 2 не будет (₂₁= 0, ₁₂= 1) и вся схема зарядится до двойного напряжения по отношению к воздействующей волне U₀=1 (рис.5,б). Это обусловлено тем, что при t =  частота изменения воздействующего прямоугольного импульса напряжения равна нулю и нагрузка в узле 3 схемы представляет собой бесконечно большое сопротивление (X_C=1/C), т.е. линия не нагружена. Следует также отметить кратковременное понижение напряжения в узлах 2 и 3 исследуемой схемы при приходе отрицательной отраженной волны от третьего узла (при _фр  0  , X_C0 и следовательно ₃₂= -1).

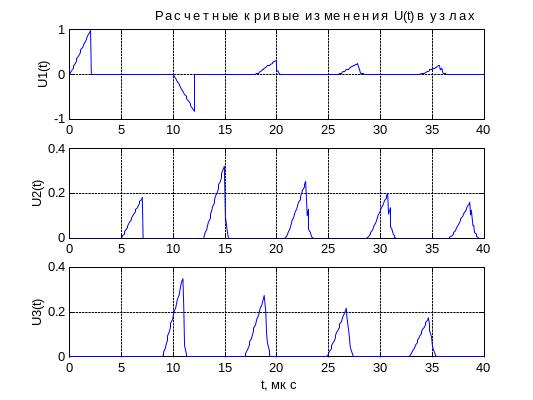
Рис.4. Расчетные кривые изменения напряжения в узлах исследуемой схемы

при воздействии импульса напряжения конечной длительности (_и= 2 мкс)

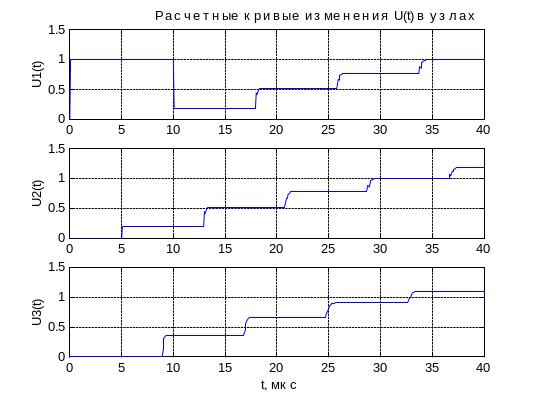
а)

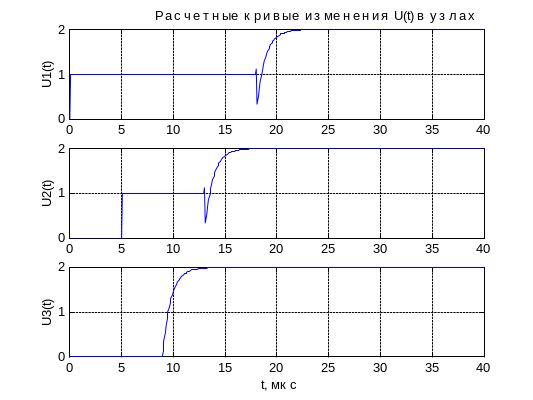
б)

Рис. 5. Расчетные кривые изменения напряжения в узлах исследуемой схемы

при воздействии импульса напряжения бесконечной длительности и

варьировании значений Z_В1 и Z_В2 : а) - Z_В1 =10Z_В2 , б) - Z_В1 = Z_В2