7

Лекция 5 экономическая динамика и ее моделирование

1. Показатели экономической динамики

Динамика – изменение состояния системы во времени. Время в экономической динамике может рассматриваться как непрерывное или дискретное. Непрерывное время удобно для моделирования, так как позволяет использовать аппарат дифференциального исчисления. Дискретное время удобно для приложений, поскольку статистические данные всегда дискретны и относятся к конкретным промежуткам или моментам времени. Большинство моделей экономи­ческой динамики существуют как в непрерывном, так и в дискретном вариантах.

Показатели, характеризующие динамику экономического объекта, - это абсолютные темпы роста и прироста.

Если рассматривается зависящая от времени величина - дискретная, то абсолютный прирост, темп роста и темп прироста определяются соотношениями:

.

Если темп прироста неизменен во времени, то динамика показателя может быть записана как .

Если есть непрерывная функция времени, то рост ее с постоянным темпом записывается как , где - непрерывный темп прироста

.

Рассмотрим величины темпов прироста для сумм и произведений показате­лей.

Пусть показатель есть сумма и , растущих соответственно, с постоянными непрерывными темпами и , причем _. Тогда

.

Поскольку , величина в квадратных скобках стремится к единице, и темп прироста суммы приближается к темпу быстрее растущего составляю­щего, т.е. к .

Для произведения имеем

.

Если и - дискретные темпы прироста, то и , то

.

При малых и величина пренебрежимо мала, и темп прироста произведения приближенно равен сумме темпов прироста сомножителей.

2. Связь объемных и темповых показателей функции Кобба-Дугласа

Связь объемных и темповых величин рассмотрим на примере производст­венной функции Кобба-Дугласа. Пусть - непрерывные функции времени, - непрерывные темпы их прироста.

Тогда объемная ПФ с нейтральным техническим прогрессом (при постоянном тем­пе последнего, равном ) имеет вид:

.

Логарифмируя эту зависимость, получаем:

.

Откуда

.

Следовательно

,

где и - эластичности выпуска по капиталу и труду соответственно.

Эта линейная формула характеризует вклад темпов прироста факторов про­изводства в общие темпы прироста дохода, а показатель характеризует вклад технического прогресса.

3. Примеры моделей экономической динамики

Рассмотрим два примера моделей макроэкономической динамики, реали­зующих дискретный и непрерывный подходы. В обоих случаях модели носят весь­ма общий, абстрактный характер. На этих моделях удобно продемонстрировать простейший аппарат дискретного и непрерывного динамического моделирования, продемонстрировать проблемы макроэкономической динамики.

3.1. Паутинообразная модель

Эта модель позволяет исследовать устойчивость цен и объемов товаров на рынке, описываемом традиционными кривыми спроса и предложения (см. рис.1) при наличии запаздывания во времени (лага).

Пусть производители определяют предложения товара в текущем периоде на основе цен, установившихся в предшествующем пе­риоде, т.е. . Действительно, решение об объеме производства принимается с учетом текущих цен, но производственный цикл имеет определенную продолжительность, и соответствующее этому решению предложение появится на рынке по окончании данного цикла.

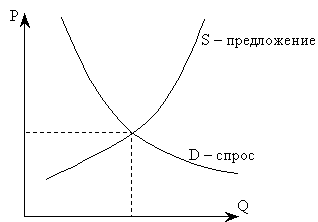
Рис. 1. Паутинообразная модель

Объем спроса на товар зависит от цены товара в данном периоде, т.е. . Таким образом, динамику цены можно описать системой уравнений:

,

( - равновесное состояние системы) или одним уравнением

.

Из этого уравнения можно найти значение цены в текущий момент времени по известному значению в предшествующий момент времени.

Схема решения очень проста:

где - обратная функция спроса.

В качестве примера рассмотрим путинообразную модель, в которой функции спроса и предложения линейны:

; ; .

Здесь , так как функция предложения возрастающая; так как функция спроса убывающая; , т.е. (считаем, что при нулевой цене спрос превышает предложение). Уравнение, описываю­щее динамику такой системы, имеет вид:

, или .

Найдем сначала равновесную цену и равновесный объем производства . Они должны удовлетворять уравнениям

,

откуда

и .

Теперь исследуем поведение цен и объемов производства в том случае, если начальная точка не совпадает с равновесной. Вначале эту задачу можно решить графически (см. рис. 2). Из графического анализа можно сделать следующие выво­ды. Если кривая предложения наклонена круче, чем кривая спроса , то равновесие на таком рынке будет устойчивым. Если же кривая спроса наклонена круче, чем кривая предложения , то равновесие на рынке будет неустойчивым (процесс расходится). Наконец, при равном наклоне кривых спроса и предложения цены на рынке будут испытывать регулярные колебания с постоянной амплитудой.

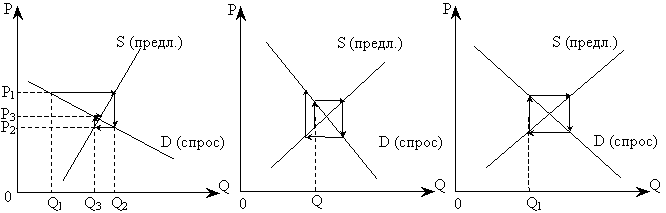
Рис. 2. Графическое решение задачи

Итак, определяющим моментом для устойчивости системы является менее сильная сглаживающая реакция на изменение цены той функции, которая имеет временной лаг (здесь - функция предложения).

В реальности при бесконечно возрастающих колебаний, конечно, не будет, так как при больших отклонениях от равновесия линейное приближение становится нереалистичным. В более реалистической нелинейной модели устанав­ливаются нелинейные колебания большой, но конечной амплитуды, которые явля­ются прообразом экономических циклов подъема и спада производства.