Вычислительные методы

Контрольная работа №1 new

Вариант №18

Задача №1. Пусть для функции f(x) = x ln(x) в точке x = 0.1 численно подсчитывается первая производная с помощью центральной разности. Считая шаг конечной разности h = h_k = 2^1–k, k = 1,2,…, найти такое k, при котором погрешность минимальна.

Задача №2. Найти первую и последнюю координаты собственного вектора x₇ матрицы , i, j = 1,…15, пользуясь MATLAB функцией eig.

Задача №3. Найти , решая систему дифференциальных уравнений на отрезке [0,1] методом Рунге-Кутта четвертого порядка точности. Считать, что на отрезке [0,1] выбрана равномерная сетка вида: 0 = x₁ <x₂ < … < x₂₀₁ = 1 и .

Вычислительные методы

Контрольная работа №1 new

Вариант №19

Задача №1. Пусть для функции f(x) = x e^x в точке x = 1 численно подсчитывается вторая производная с помощью формулы со вторым порядком точности. Считая шаг конечной разности h = h_k = 2^1–k, k = 1,2,…, найти такое k, при котором погрешность минимальна.

Задача №2. Найти первую и последнюю координаты собственного вектора x₇ матрицы , i, j = 1,…10, пользуясь MATLAB функцией eig.

Задача №3. Найти , решая систему дифференциальных уравнений , i = 1,…,200 на отрезке [1,3] методом Рунге-Кутта четвертого порядка точности. Считать, что на отрезке [1,3] выбрана равномерная сетка вида: 1 = x₁ <x₂ < … < x₁₅₁ = 3 и .

Вычислительные методы

Контрольная работа №1 new

Вариант №20

Задача №1. Пусть для функции f(x) = xsh(x) в точке x = 1 численно подсчитывается вторая производная с помощью формулы со вторым порядком точности. Считая шаг конечной разности h = h_k = 2^1–k, k = 1,2,…, найти такое k, при котором погрешность минимальна.

Задача №2. Найти первую и десятую координаты собственного вектора x₇ трехдиагональной матрицы , i = 1,…100, , i = 1,…,99, , i = 2,…,100, пользуясь MATLAB функцией eig.

Задача №3. Найти , решая систему дифференциальных уравнений 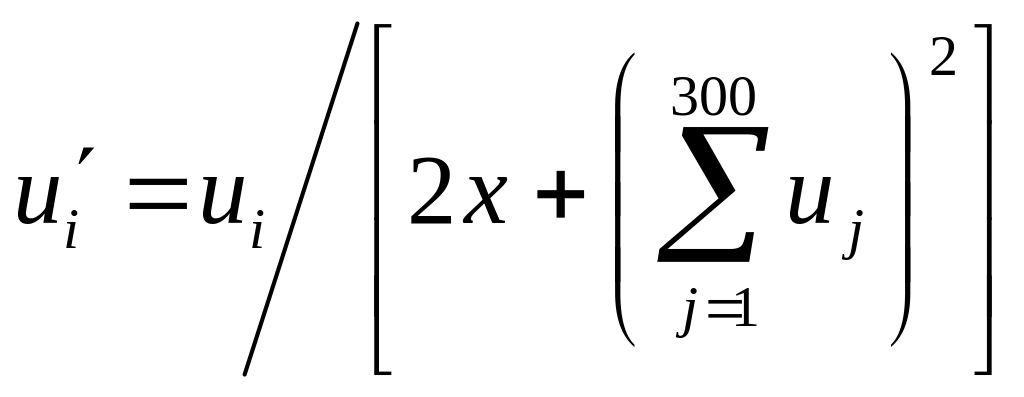, i = 1,…,300 на отрезке [1,3] методом Рунге-Кутта четвертого порядка точности. Считать, что на отрезке [1,3] выбрана равномерная сетка вида: 1 = x₁ <x₂ < … < x₁₅₁ = 3 и .

Вычислительные методы

Контрольная работа №1 new

Вариант №21

Задача №1. Найти определенный интеграл с помощью формулы трапеции на равномерной сетке 0 = x₁ < …< x₅₀₁ = 1.

Задача №2. Стартуя с отрезка [1,2], методом золотого сечения найти положение локального минимума функции при x > 0 с точностью не хуже 10^6 и количество итераций.

Задача №3. Найти , решая дифференциальное уравнение на отрезке [1,3] методом Адамса четвертого порядка точности. Считать, что на отрезке [1,3] выбрана равномерная сетка вида: 1 = x₁ <x₂ < … < x₂₀₁ = 3 и и дополнительные три значения решения в точках x₂, x₃, x₄, обеспечивающие работу метода Адамса, найдены с помощью метода Рунге-Кутта четвертого порядка.

Вычислительные методы

Контрольная работа №1 new

Вариант №22

Задача №1. Найти определенный интеграл с помощью формулы трапеции на равномерной сетке 0 = x₁ < …< x₅₀₁ = 1.

Задача №2. Стартуя с отрезка [1.8;2], методом золотого сечения найти положение локального минимума функции , где с точностью не хуже 10^6 и количество итераций.

Задача №3. Найти , решая дифференциальное уравнение на отрезке [1,3] методом Адамса четвертого порядка точности. Считать, что на отрезке [1,3] выбрана равномерная сетка вида: 1 = x₁ <x₂ < … < x₂₀₁ = 3 и и дополнительные три значения решения в точках x₂, x₃, x₄, обеспечивающие работу метода Адамса, найдены с помощью метода Рунге-Кутта четвертого порядка.